浙江省杭州第十四中學(310006) 樓思遠 周 艷

近日,筆者在課堂上講解一道關于二次曲線的切線問題時,學生提出了異議,在加以簡單的幾何解釋后學生仍有疑問,于是師生約定:各自思考后,第二天課堂展示成果,分享思路與比較哪種方法更優(yōu).根據學生展示的不同方法,師生一起通過討論分析將其整合與歸類.接著,筆者又依次給出幾道不同梯度的相關問題讓學生完成,最終取得了較好的教學效果,過程如下:

1 突發(fā)“意外”,順水推舟

課堂教學片段:

題目:已知拋物線C1:y=x2+2x和C2:y=-x2+a,若直線l同時是C1和C2的切線,則稱l是C1和C2的公切線,問:當a取什么值時,C1和C2有且僅有一條公切線?試寫出公切線的方程.

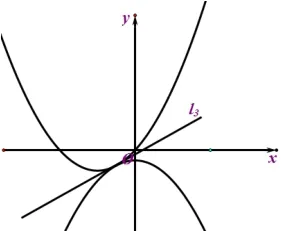
圖一

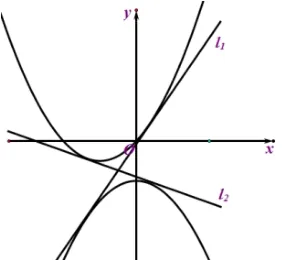
圖二

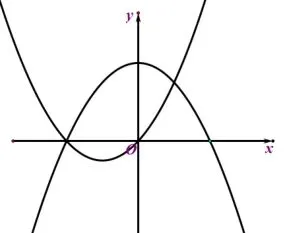
圖三

師:顯然,由題可知圖象應該如此(黑板上畫出圖一),從而列出方程解得答案.

生1:老師我認為圖象往下移一點(圖二)也只有一條切線l1.

師:(略微一愣,微笑的畫出了另一條切線l2),從圖象可以看出這種情況有兩條切線.

生2:那如果向上移動呢,是不是也是兩條?

師:(在黑板上作出圖三)因為開口大小的關系,從圖象可以看出這種情況沒有切線.

生2:可是根據圖二的畫法,圖三的圖象左右兩側也該有兩條切線才對啊?(臺下有附和聲).

筆者一時也想不出更好的辦法來解釋,這個“意外”讓課堂陷入了沉寂,筆者隨即靈機一動,表示要與學生比比誰更快的找到解決方案,有想法的可以在明天為大家展示,學生的熱情一下被激發(fā)出來,個個躍躍欲試……

2 趁熱打鐵,揭示本質

第二天的課堂上,筆者先讓學生踴躍發(fā)言,在歸納整理后于黑板上寫下三種具有代表性的解題思路,具體如下:

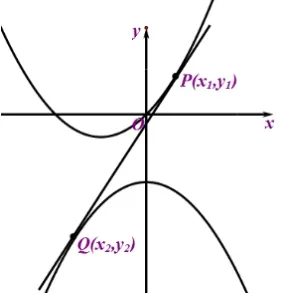
法一圖

法二圖

法三圖

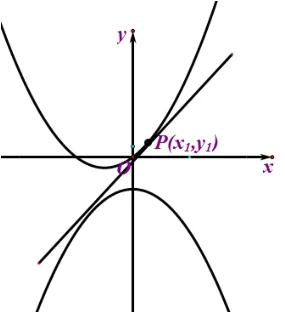
法一(多點開花,兩面夾擊)

設切點為P(x1,y1),Q(x2,y2),記f(x)=x2+2x,g(x)=-x2+a,則f′(x)=2x+2,g′(x)=-2x,根據P點坐標求得lPQ:y=(2x1+2)x-x21;根據Q點坐標求得:lPQ:y=-2x2x+(a+x22),因為是同一條公切線,對比系數(shù)知:

(1)(2)?+2x1+(a+1)=0,將x1看成主元,得Δ=-4-8a,下面分類討論之:當Δ＞0,即時,x1有兩實數(shù)解,分別對應不同的x2,故有兩條切線,即圖二的情況;當Δ=0,即時,一條切線,即圖一的情況;當Δ＜0,即時,沒有切線,即圖三的情況.

法二(二次判別,一招制勝):

設f(x)=x2+2x上的一個切點為P(x1,y1),則過P的直線方程為:lp:y=(2x1+2)x-x21,聯(lián)立方程組得:x2+(2x1+2)x-(x21+a)=0.

要使lp與y=-x2+a相切,應滿足判別式Δ1=0,即再將其看成關于x1的二次方程,則x1的解的個數(shù)對應切線的條數(shù),解得Δ2=-4-8a,以下同法一.

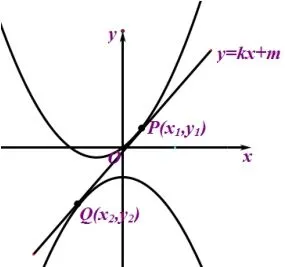
法三(化繁為簡,穩(wěn)中求進):

設切點分別為P(x1,y1),Q(x2,y2),直線方程為l:y=kx+m,由兩切點皆在直線l上得,相減得:

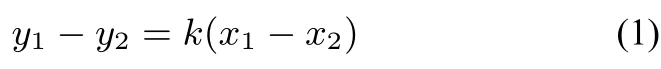
同理,由兩點在各自曲線上得:

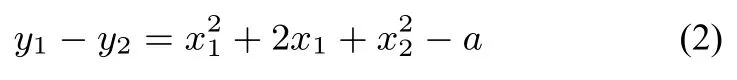
由兩點處切線斜率相等得:

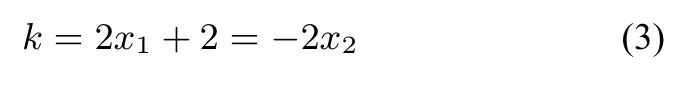
筆者與學生一起對三種方法進行分析與比較后總結如下:

(1)法一計算量不大,思路較為巧妙,從中可歸納出解決公切線問題的關鍵:根據兩條曲線在切點處的導數(shù)分別表示出該公切線,利用對應系數(shù)相等找到等量關系,再具體求解;

(2)法二將問題轉化為了熟悉的二次函數(shù)圖象問題,學生比較容易上手,但是運用兩次判別式對思維層次要求較高,若將拋物線換為橢圓或雙曲線,那么判別式的計算就比較繁瑣,因此該法有一定局限性;

(3)法三則是典型的的解析幾何的方法,在具體的解答過程中,變量較多,消元的過程需要預判與耐心,許多學生會半途而廢.

在解開了課堂疑惑后,學生們的熱情仍然高漲,筆者認為應該趁熱打鐵繼續(xù)加深學生對該類問題的認識與理解,便給出了如下問題:

(2018年浙江學考22)若不等式2x2-(x-a)|x-a|-2≥0對于任意x∈?恒成立,則實數(shù)a的最小值是____.

有了之前的鋪墊,學生很快便給出了解法:

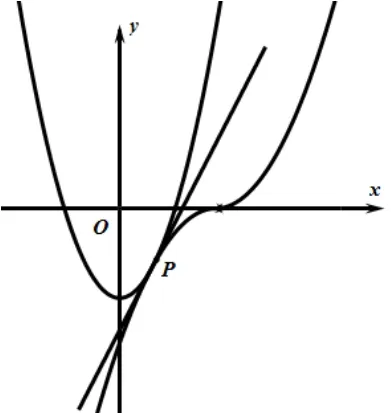
解:原不等式等價于2x2-2≥畫出臨界位置(右圖),此時兩個切點重合,設為P(x0,y0),由點P落在曲線y=2x2-2上知

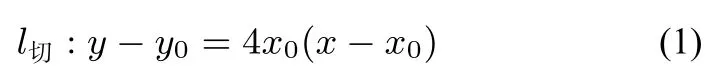
由點P落在曲線y=-(x-a)2上知

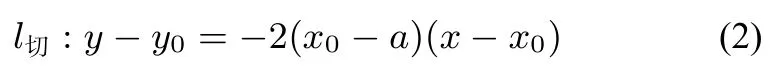
因為切線為同一條直線,對比系數(shù)知:a=3x0,代回原曲線方程解得

(2013年華約自主招生5)已知點A在直線y=kx上,點B在直線y=-kx上,其中k＞0,|OA|·|OB|=k2+1,且A,B在y軸同側.

(1)求AB的中點M的軌跡C;

(2)若曲線C與拋物線x2=2py(p＞0)相切,(a)求證:兩切點分別過兩定直線;(b)求過兩切點的切線方程.

解:(1)C:

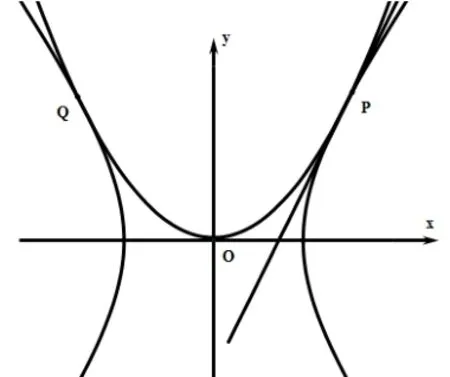
(2)設兩個切點分別為P(x0,y0),Q(x1,y1),考慮P點的情況:由P在雙曲線上得l切:x0x-=1,即

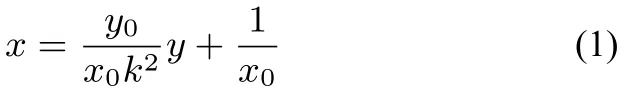
由P在拋物線上得l切:x0x=p(y0+y),即

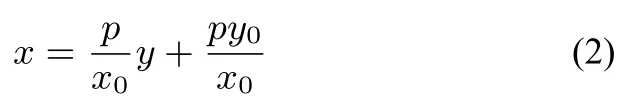
因為兩條切線為同一條直線,對比系數(shù)知:

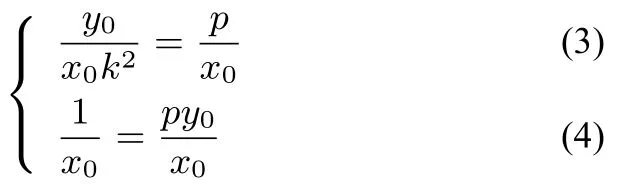
解得y0=k,代回雙曲線方程知因此切點P在定直線上,過點P的切線方程為Q點類似.

總結:上述兩題皆是切點重合的情況,根據兩條曲線在切點處的導數(shù)分別表示出該公切線,利用對應系數(shù)相等找到等量關系,即可順利求解.

3 更進一步,提升層次

至此,學生們已經體會到了思維的樂趣與成功的喜悅,筆者不失時機的給出兩個切點不重合的問題,希望能百尺竿頭,更進一步:

(2019年浙江學考24)如圖,不垂直于坐標軸的直線l與拋物線y2=2px(p＞0)有且只有一個公共點M.

(1)當M的坐標為(2,2)時,求p的值及直線l的方程;

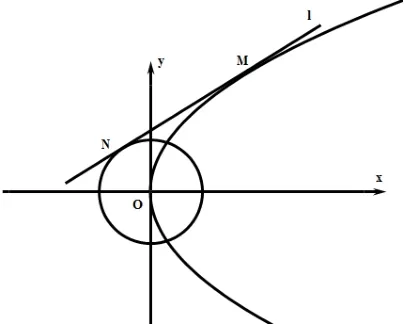
(2)若直線l與圓x2+y2=1相切于點N,求|MN|的最小值.

解:(1)略;(2)設N(x1,y1),M(x2,y2),根據切點N知lMN:x1x+y1y=1,即y=根據切點M知lMN:y2y=p(x+x2),即因為lMN表示同一條直線,根據對應系數(shù)相等得:

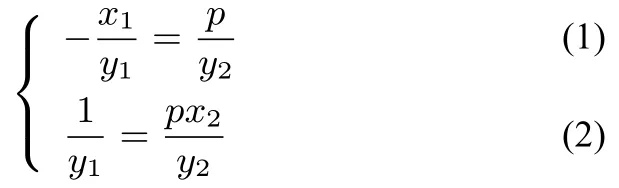
解得

將點M代入根據N點坐標求得的切線方程lMN:x1x+y1y=1中得x1x2+y1y2=1,解得

根據(3)(4)知:

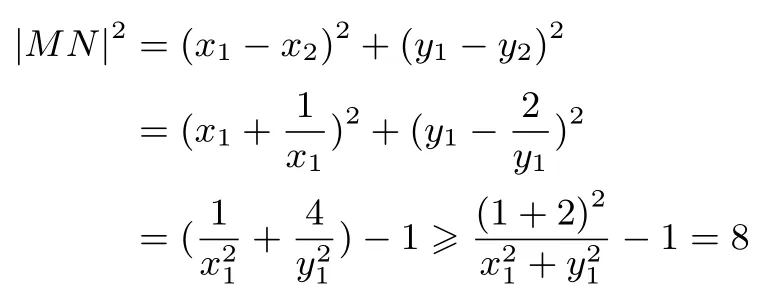
解:設P(x1,y1),Q(x2,y2),只需證明:

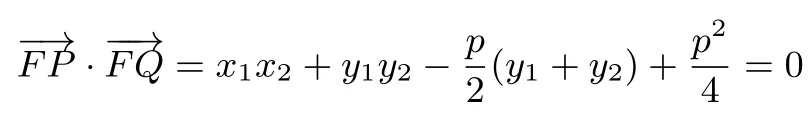
由題知:

根據切點P知lPQ:即y=根據切點Q知lPQ:x2x=p(y2+y),即y=因為lPQ為同一條直線,根據對應系數(shù)相等得

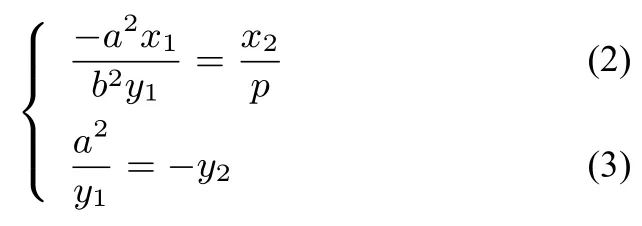
解得

將點P(x1,y1)代入根據Q點坐標求得的切線方程lPQ:x2x=p(y2+y)中得:

根據(1)(4)(5)(6)知:

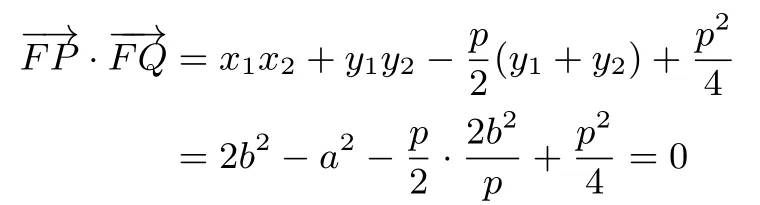
以第二題為例:在具體的解題過程中,大部分學生無法求出y1+y2的值.在筆者的啟發(fā)下,利用“將切點P代入用切點Q表示的切線方程中”這一點才證得結論,師生在共同討論后進一步完善了該類問題的方法模型:

(1)若是在兩個切點重合,根據兩條曲線在切點處的導數(shù)分別表示出該公切線,利用對應系數(shù)相等找到等量關系.

(2)若是兩個切點不重合,一方面可根據兩條曲線在各自切點處的導數(shù)分別表示出該公切線,利用對應系數(shù)相等找到等量關系,另一方面可利用“其中一個切點位于用另一個切點坐標表示的切線上”這一點來發(fā)掘隱含關系.

4 反思總結,螺旋上升

正是學生通過直觀想象對圖形結構提出了質疑,才引發(fā)了后面一系列有意義的討論與思考.因此,教師在上課之前應充分考慮學生的思維視角,對可能出現(xiàn)的情況做各種預設,基于記憶與理解的時效性,對學生課堂提出的問題足夠重視并及時給出明確的解答,這樣才能讓整個教學過程少點往復,多點效率.

維果斯基的“最近發(fā)展區(qū)理論”認為學生的發(fā)展有兩種水平:一種是現(xiàn)有水平,即獨立活動時所能達到的解決問題的水平;另一種是可能的發(fā)展水平,即通過教學指導之后能到達到的水平.兩者之間的差異就是最近發(fā)展區(qū).本次課堂教學不僅僅滿足于解決學生提出的問題,更進一步,還著眼于學生的最近發(fā)展區(qū),及時提供不同梯度的相關內容進行課堂討論,從而調動他們的積極性.在整個過程中,學生通過對解題模式的正遷移,充分領略了解題策略的橫向擴展與縱向伸延,進而在潛移默化中內化為數(shù)學解題經驗.

最后,“直觀想象”與“邏輯推理”這二者的辨證統(tǒng)一也在課堂得到體現(xiàn):有時對圖形的直觀想象并不能精準的刻畫出數(shù)學問題的本質,此時需從代數(shù)角度進行嚴格的邏輯推理來獲得精確的證明,而在證得結論后,需再次回到圖形的角度透析本質,加深理解.因此,“直觀想象”與“邏輯推理”二者相得益彰,這與“數(shù)缺形時少直觀,形少數(shù)時難入微;數(shù)形結合百般好,隔離分家萬事休”的思想是完全契合的.