安徽省無(wú)為縣牛埠中學(xué)(238351) 朱小扣

1.換元法的引入

例1(2016年遼寧預(yù)賽11題)已知lga+lgb+lgc=0,證明

證明 因?yàn)閘ga+lgb+lgc=0,故a,b,c＞0,且abc=1.當(dāng)a=b=c=1時(shí),有

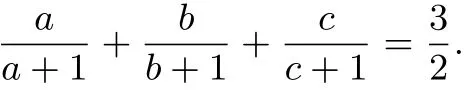
當(dāng)a,b,c不全相等時(shí),則a,b,c中至少有一個(gè)小于1的.不妨設(shè)0＜c＜1.令

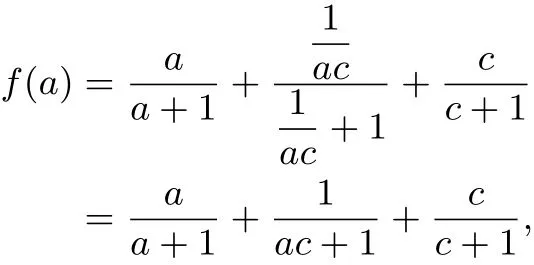
則

故g(b)為增函數(shù).由于

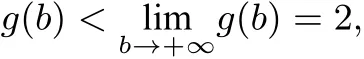
因此,1＜f(a)＜2.故命題得證.

上述解法是命題組提供的答案,筆者按此答案在班級(jí)講授時(shí),發(fā)現(xiàn)學(xué)生看起來(lái)耗時(shí)耗力,不好理解.那么有沒(méi)有做和理解起來(lái)都更簡(jiǎn)單的解法可以繞過(guò)求導(dǎo)呢?筆者經(jīng)過(guò)研究發(fā)現(xiàn)換元法可以替代求導(dǎo)法,原題可以通過(guò)換元法完美的解決,過(guò)程如下:

證明 因?yàn)閘ga+lgb+lgc=0,故a,b,c＞0,且abc=1.

綜合(1),(2)得知原不等式成立.

故命題得證.

以上是條件換元,做代換:

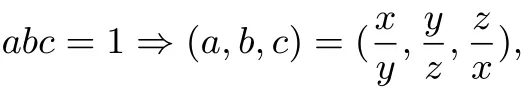
除此之外還有:

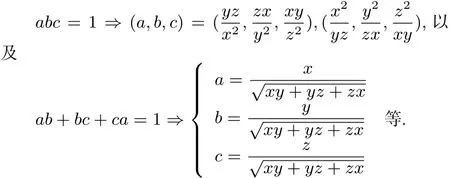
點(diǎn)評(píng) 述例題中通過(guò)將條件不等式即在abc=1的條件下,通過(guò)換元轉(zhuǎn)化成非條件不等式問(wèn)題,也將不等式的分子,分母齊次化,從而有利于問(wèn)題的解決.這種解法相比命題組所給的答案更簡(jiǎn)單,只用了簡(jiǎn)單的不等式放縮,且更容易理解,更能體現(xiàn)“大道至簡(jiǎn)”的思想.

有時(shí)候也會(huì)利用換元法將非條件不等式問(wèn)題轉(zhuǎn)化成條件不等式,如:

例3設(shè)a,b,c∈R+,求證:

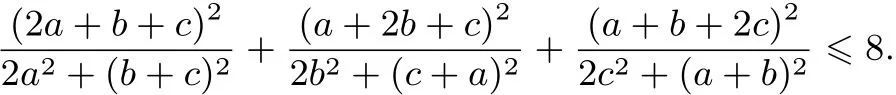
簡(jiǎn)證 不妨設(shè)a+b+c=1,則原不等式化為

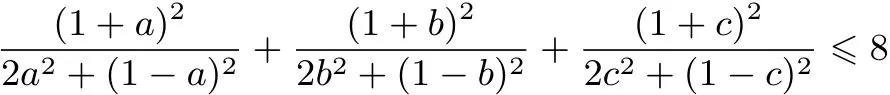
再由切線法證

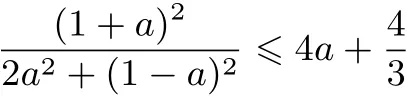
即可.

點(diǎn)評(píng) 只需考慮a+b+c=1,因?yàn)榧僭O(shè)a+b+c=s,則可設(shè) a=sa′,b=sb′,c=sc′,代入原不等式,即和 a+b+c=1的情形一樣.也就是利用換元法將非條件不等式問(wèn)題轉(zhuǎn)化成條件不等式.

2.其他換元方法

2.1 拉維換元

例4 已知△ABC三邊分別是a,b,c,求證:

a2b(a-b)+b2c(b-c)+c2a(c-a)≥0.

證明 拉維換元

令a=x+y,b=y+z,c=z+x(x,y,z∈R+),則原不等式可化為:

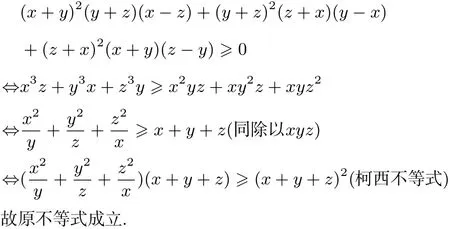
例5已知△ABC三邊分別是a,b,c,求證:a2+b2+

點(diǎn)評(píng) 拉維換元:在△ABC中,令

a=x+y,b=y+z,c=z+x(x,y,z∈R+),

這樣換元,就可以消去在三角形中的兩邊之和大于第三邊的約束,使約束的條件得到釋放,為進(jìn)一步的解決問(wèn)題打好了基礎(chǔ).

2.2 分母換元法

解 (分母換元法)令

a=y+3z,b=4x+8z,c=3x+2y,

則

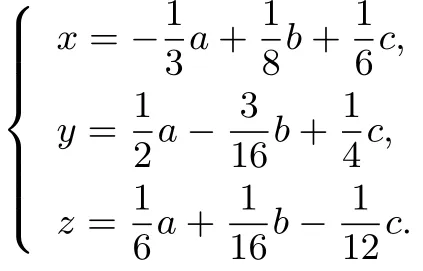
于是

當(dāng)且僅當(dāng)x:y:z=10:21:1時(shí)取等號(hào).

分母換元法還可以解決很多類(lèi)似題,又如:

點(diǎn)評(píng) 利用分母換元法,可以將復(fù)雜的分母簡(jiǎn)化,進(jìn)而運(yùn)用均值不等式使得問(wèn)題能簡(jiǎn)單的解決.分母換元法在解決此類(lèi)問(wèn)題中均達(dá)到了“釜底抽薪”的效果.

2.3 乘積換元法

例8(2017年清華大學(xué)能力測(cè)試題改編)已知x,y∈R,且5x2-4xy-y2=5,則2x2+y2的最小值是.

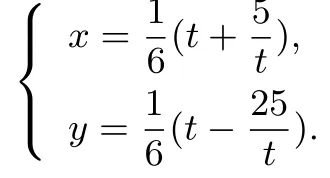
故

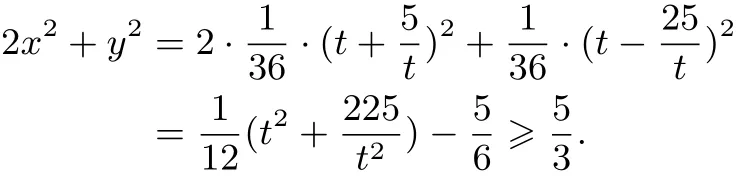
乘積換元法可以拓展,又如例7:

例9 已知x2+xy+y2=1,求x2+3xy+2y2的范圍.

提示 注意到

x2+3xy+2y2=(x+y)(x+2y),

點(diǎn)評(píng) 例8中利用設(shè)其中一個(gè)因式為t,得到一個(gè)方程組,解出x,y用t表示,以達(dá)到化二元為一元的效果,使得問(wèn)題得以解決.而例9是乘積換元法的逆向運(yùn)用,是對(duì)乘積換元法能力的要求進(jìn)一步的提升.

2.4 增量換元法

證明 設(shè)

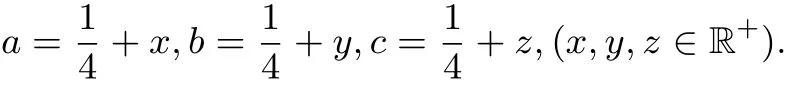
因?yàn)?/p>

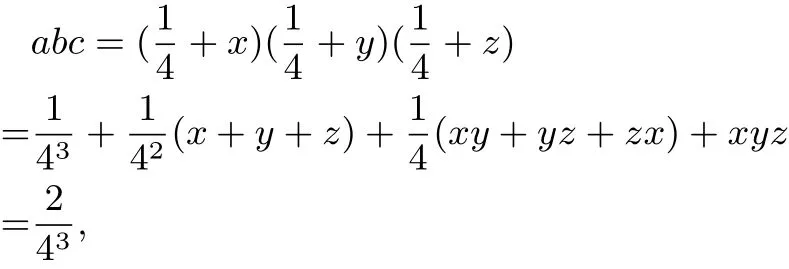
所以

例11 設(shè)a,b,c是△ABC三邊的長(zhǎng),求證:a2(b+ca)+b2(c+a-b)+c2(a+b-c)≤3abc

提示 不妨設(shè)a≥b≥c,令a=c+m,b=c+n(m≥n≥0)即可.

點(diǎn)評(píng) 增量換元法通俗易懂,是一種很實(shí)用的方法,通過(guò)增量換元的化歸可以讓題目變得更簡(jiǎn)單,同時(shí)也進(jìn)一步延拓了這類(lèi)不等式的解題方法.增量換元法解類(lèi)似的題有很多,在此不再一一例舉.

3.換元升級(jí):常數(shù)變?cè)?/h2>

例12 已知a,b∈R+,且3a+4b=1,求的最小值.

解

例13 (2016年河北預(yù)賽13題)設(shè)正數(shù) x,y滿(mǎn)足x3+y3=x-y,求使x2+λy2≤1恒成立的實(shí)數(shù)λ的最大值.

解 由正數(shù)x,y滿(mǎn)足x3+y3=x-y知x＞y＞0,

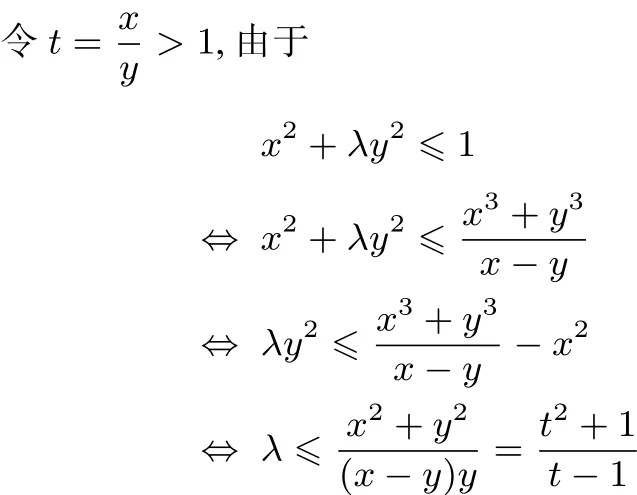
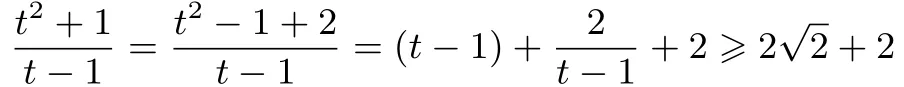
點(diǎn)評(píng) 通過(guò)易常為變,可以將不等式變?yōu)辇R次,進(jìn)一步變成求一元函數(shù)的最值問(wèn)題使問(wèn)題得到完美的解決,但像例13難度較大,不易想到.所以我們?cè)谧鲱}時(shí),應(yīng)不斷采用變化的思維去考慮問(wèn)題,最終達(dá)到對(duì)常數(shù)變?cè)ǖ恼莆?

總結(jié) 通過(guò)對(duì)一道預(yù)賽題的另解,讓我們認(rèn)識(shí)到換元法功能的強(qiáng)大.實(shí)際上,換元法的本質(zhì)是轉(zhuǎn)化,通過(guò)元之間的轉(zhuǎn)化過(guò)渡,使問(wèn)題能由繁變簡(jiǎn),由難變易,通過(guò)換元能讓學(xué)生更加體會(huì)數(shù)學(xué)中的千變?nèi)f化的美.道法自然,解法也應(yīng)自然.學(xué)生應(yīng)在不斷做題中,在方法的不停的交匯中,達(dá)到自身水平的提高,這樣才會(huì)在解題時(shí),找到渾然天成的解題方法.

猜你喜歡

換元預(yù)賽乘積

因式分解的整體思想及換元策略

中學(xué)生數(shù)理化·七年級(jí)數(shù)學(xué)人教版(2021年12期)2021-12-31 05:16:38

一道四川省預(yù)賽題的探究

中等數(shù)學(xué)(2021年7期)2021-11-22 07:26:04

乘積最大

小學(xué)生學(xué)習(xí)指導(dǎo)(中年級(jí))(2021年3期)2021-04-06 09:12:08

2018瑞士數(shù)學(xué)奧林匹克(預(yù)賽)

中等數(shù)學(xué)(2020年3期)2020-08-24 07:59:24

Dirichlet級(jí)數(shù)及其Dirichlet-Hadamard乘積的增長(zhǎng)性

數(shù)學(xué)年刊A輯(中文版)(2018年1期)2019-01-08 01:58:22

第九屆陳省身杯全國(guó)高中數(shù)學(xué)奧林匹克預(yù)賽

中等數(shù)學(xué)(2018年4期)2018-08-01 06:36:34

“換元”的巧妙之處

中學(xué)教學(xué)參考·理科版(2017年8期)2018-02-24 21:32:13

三角換元與基本不等式的“爭(zhēng)鋒”

中學(xué)生數(shù)理化·高三版(2017年2期)2017-04-21 10:50:59

三角換元與基本不等式的“爭(zhēng)鋒”

福建中學(xué)數(shù)學(xué)(2017年1期)2017-04-21 10:35:29

復(fù)變?nèi)呛瘮?shù)無(wú)窮乘積的若干應(yīng)用

數(shù)學(xué)學(xué)習(xí)與研究(2015年15期)2015-05-30 01:17:26

中學(xué)數(shù)學(xué)研究(廣東)2018年1期

中學(xué)數(shù)學(xué)研究(廣東)的其它文章

例談恰當(dāng)分離策略在壓軸題中的應(yīng)用

2017年高考文科數(shù)學(xué)全國(guó)卷(I)第12題的研究

一道廣東高考數(shù)列試題的解法探源及高觀點(diǎn)背景剖析

對(duì)一道高考解幾壓軸試題的探析*

高考含有超越函數(shù)壓軸題的常用解題策略

對(duì)一道高考題的反思與探究