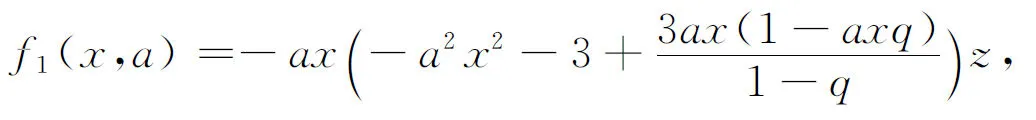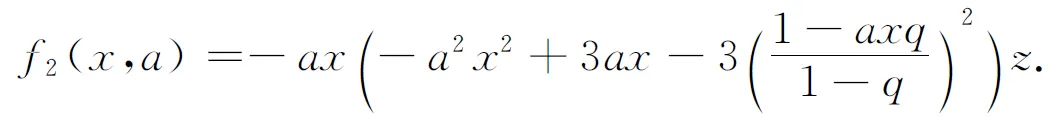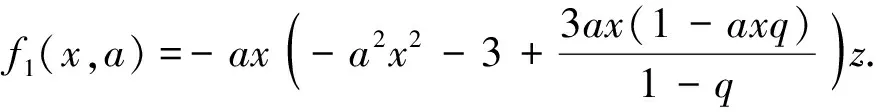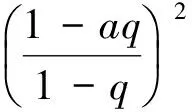一個q-級數(shù)不等式
,
(淮陰師范學(xué)院 數(shù)學(xué)科學(xué)學(xué)院, 江蘇 淮安 223300)
0 引言
q-級數(shù),也稱為基本的超幾何學(xué)級數(shù),它在許多領(lǐng)域有著非常重要的作用,比如:數(shù)論,群論,根系,李代數(shù)及物理學(xué)中的量子群表示等.由于其重要性,到目前為止建立了許多的q-級數(shù)恒等式[1-3].但是有些q-級數(shù)其和不易求得,故運用其他方法來研究q-級數(shù)是有意義的.在文[4]中,Wang使用不等式技巧研究了一個q-級數(shù),獲得了關(guān)于q-級數(shù)的一個新的不等式,即
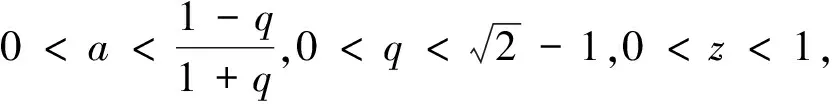
成立,其中
當(dāng)a=q時,上述不等式成立(關(guān)于[gi(x,a);q]∞(i=1,2)定義見下節(jié)).
本文受此啟發(fā),獲得了關(guān)于q-級數(shù)的一個新的不等式,拓展了文[4]的結(jié)果.
1 主要引理
為得到本文的主要結(jié)果,在本節(jié)我們先給出下列定義,引理及其證明.
定義1 如果g(x)是[0,1]上的一個函數(shù),我們定義
[g(x);q]n=(1-g(q0))(1-g(q1))…(1-g(qn-1))
[g(x);q]∞=(1-g(q0))(1-g(q1))…(1-g(qn))…
若g(x)=ax,則有 [g(x);q]n=(1-a)(1-aq)…(1-aqn-1)=(a;q)n.
引理1[4]如果0 令 下證h1(t)<0. 由于 又令 g(t)=(1+2q)t2-3t+3(1-q), 因為 則 Δ=9-12(1+2q)(1-q)=3[8q2-4q-1]<0, 故g(t)>0,從而h1(t)<0.再證h1(t)>-3. 由于 3t>(1+2q)t2,通過變形有 -(1-q)t2-3(1-q)+3t(1-qt)>-3(1-q), 則 下證h2(t)<0.由于 令 k(t)=[3q2+(1-q)2]t2-3(1+q2)t+3. Δ=9(1+q2)2-12[3q2+(1-q)2]=9(1-q2)2-12(1-q)2<0, 再證h2(t)>-4,事實上 又顯然 [3q2+(1-q)2]t2-3(1+q2)t<0, 故有 [3q2+(1-q)2]t2-3(1+q2)t+3-4(1-q)2<0. 通過變形有 (1) 對此不等式重復(fù)用n-1次,可得 R(a,z)≤[f1(x,a);q]nR(aqn,z),n=1,2,… 令n→∞,則qn→0.故由引理2我們有 R(a,z)≤[f1(x,a);q]∞R(0,z) (2) 再利用引理1,可得 對上述不等式重復(fù)用n-1次,可得 R(a,z)≥[f2(x,a);q]nR(aqn,z),n=1,2,… 令n→∞,則由引理3,得 R(a,z)≥[f2(x,a);q]∞R(0,z) (3) 結(jié)合(2),(3)有 [f2(x,a);q]∞R(0,z)≤R(a,z)≤[f1(x,a);q]∞R(0,z) (4) 由引理2與引理3,易得 0<[f1(x,a);q]∞<1,0<[f2(x,a);q]∞<1. 令a=q,再次結(jié)合(3),(4)兩式得到下面不等式, (5) 結(jié)合(4),(5)得 即 推論1 在定理1的條件下,我們有 其中 證明 (6) (7) 于是由(1),(6)和(7)式得 [1]Hardy G H,Littlewood J E,Polya G.Inequalities[M].Cambridge: Cambridge University Press,1952. [2]Gasper G.Lecture Notes for an Introductory Minicourse onq-Series[M].New York: Spring-Verlag.1995. [3]Gasper G,Rahman M.Basic Hypergeometric Series,Encyclopedia of Mathematics and Its Applications[M].Cambridge: Cambridge University Press,1990. [4]Wang M J.An Inequality about q-series[J].J Inequal Pure and Appl Math,2006,7(4): 1-7.
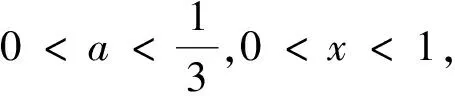
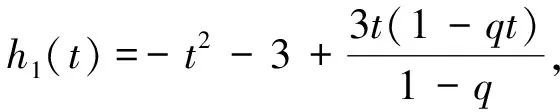
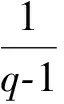
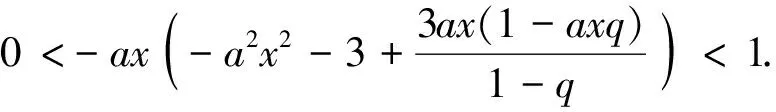

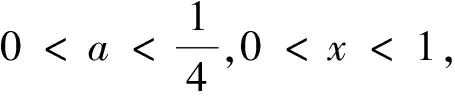

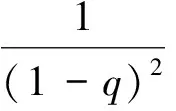
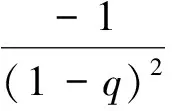
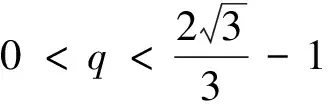
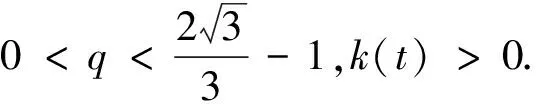

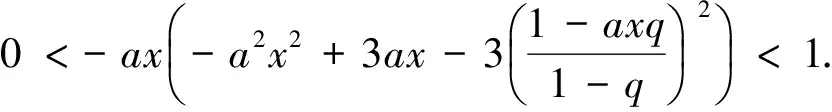
2 主要結(jié)果