毛世勤

(青島市城陽第一高級中學)

求解三角函數(shù)題時,往往會因為沒有挖掘隱含條件而出現(xiàn)各種各樣的錯誤,因此歸類整理三角函數(shù)中的常見解題誤區(qū)就顯得非常重要.本文結(jié)合例題進行剖析,旨在幫助學生明確“誤”之因,認識“誤”之道.

1 沒有充分考慮角的取值范圍

本題如果利用正弦值分析(解法1),則極易出錯;如果利用余弦值分析(解法2)或者利用正切值分析(解法3),則不易出錯.請想一想,為什么?

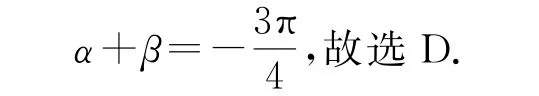
求解本題的關(guān)鍵在于充分利用根與系數(shù)的關(guān)系,將角α,β的取值范圍縮小.

2 沒有充分考慮正弦、余弦函數(shù)的有界性

在挖掘本題的隱含條件時,不但要考慮sinx的有界性,而且要考慮siny的有界性,否則極易出錯.

3 沒有充分利用銳角三角形

綜上,關(guān)注三角函數(shù)試題常見解題誤區(qū),不僅有利于加深對相關(guān)數(shù)學知識的準確理解,還有利于不斷積累解題經(jīng)驗,提高解題思維能力,有效避免一些常見錯誤,進而提升解題的速度和準確性.