劉利果

(河北省邢臺市沙河市第三中學(xué),河北 邢臺 054100)

拋物線中平行四邊形的存在性問題,是中考的一個難點,也是熱點,常常以壓軸題的形式出現(xiàn).如何突破這一類試題呢?筆者以2016年安順市一道中考題為例進行探究.

1 試題呈現(xiàn)

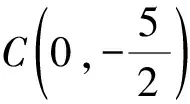
(1)求拋物線的解析式.

(2)在拋物線的對稱軸上有一點P,使PA+PC的值最小,求點P的坐標(biāo).

(3)若M為x軸上一動點,在拋物線上是否存在一點N,使A,C,M,N四點構(gòu)成的四邊形為平行四邊形?若存在,求點N的坐標(biāo);若不存在, 請說明理由[1].

2 思路分析

第(1)(2)問略.第(3)問:①如圖1所示,AC為對角線時,取AC中點O′,連接M4O′,交拋物線于點N4;如圖2所示,若AC為邊,平移AC得到另外三種情況.過四邊形頂點作橫平堅直線 (平行于坐標(biāo)軸)構(gòu)造全等三角形解決問題.

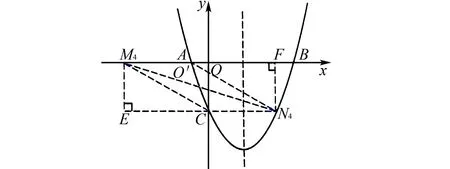
圖1 AC為對角線

②設(shè)M(x,0),分別以AC,AM,AN為對角線,分三種情況根據(jù)平行四邊形兩組相對頂點橫坐標(biāo)之和相等,縱坐標(biāo)之和也相等,表示出點N的坐標(biāo),代入拋物線解析式求解即可.

圖2 AC為邊

3 一題多解

(3)解法1 存在點N,使A,C,M,N四點為頂點構(gòu)成的四邊形為平行四邊形.

①當(dāng)AC為邊時,如圖2所示,若點N在x軸下方.

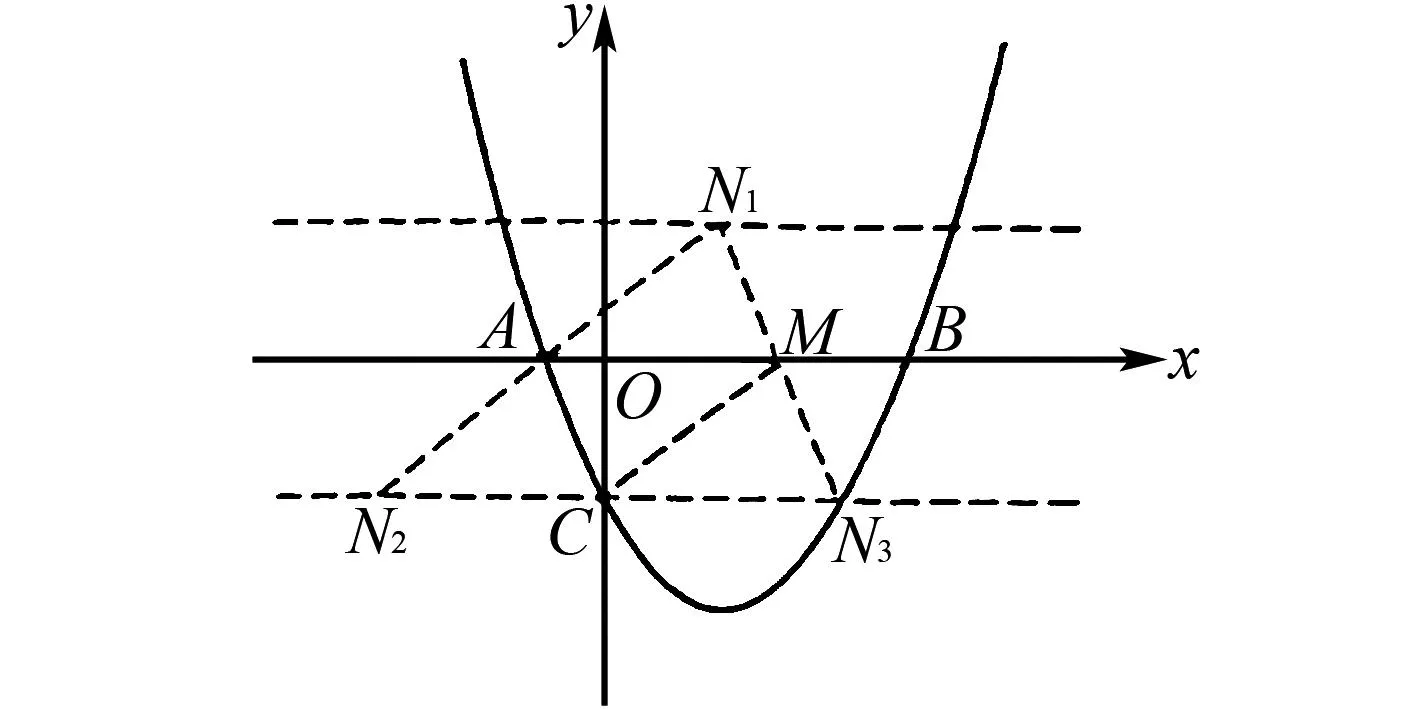
圖3 讓M運動

∵AC=M2N2,∠CAO=∠N2M2D,∠COA=∠N2DM2,

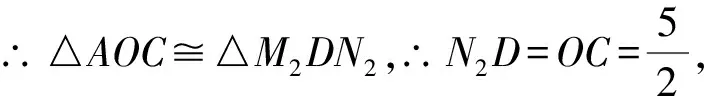
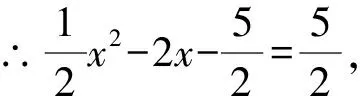
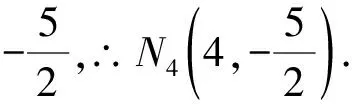
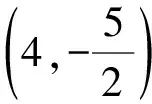
解法2設(shè)M(x,0),N(xN,yN).

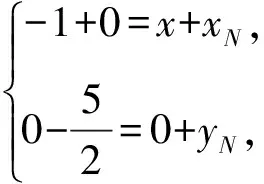
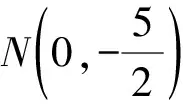
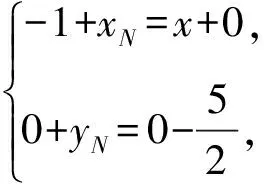
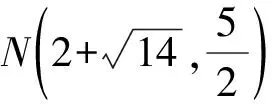
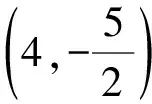
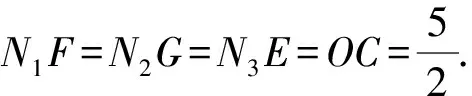
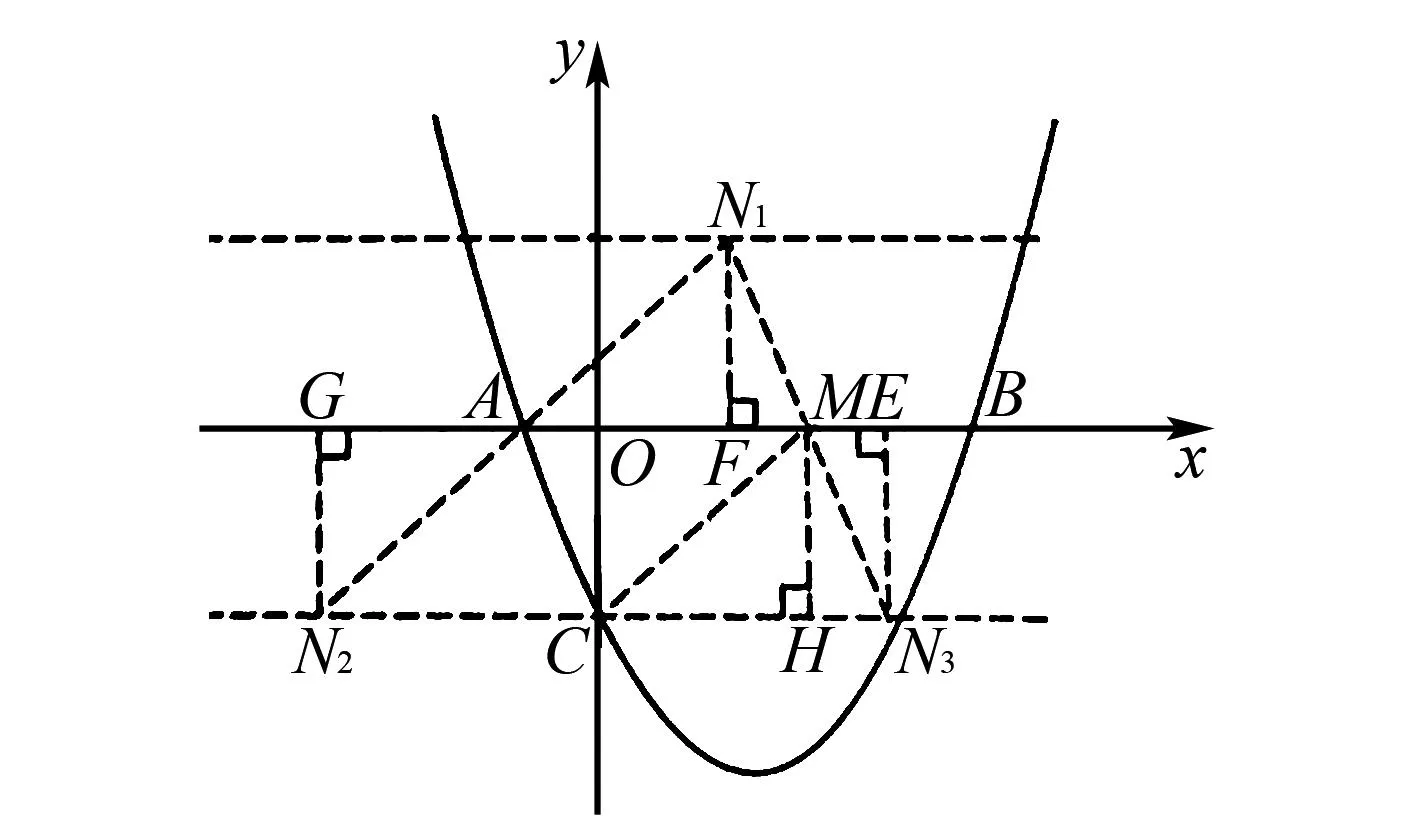
圖4 探究點N的路徑

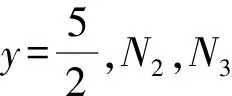
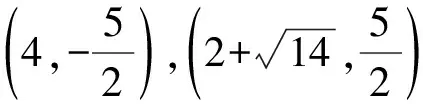
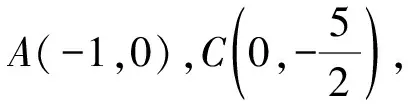
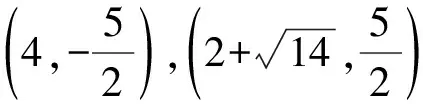
對于平行四邊形的存在性問題中已知兩個定點,先虛擬一個動點,圍成一個三角形, 過三角形的每一個頂點畫對邊的平行線,三條直線兩兩相交,就可以確定平行四邊形的第四個頂點.按照虛擬的第三個點,第四個頂點存在三種情況.但是第四個點到底有幾個,要具體問題具體分析.