福建省莆田第一中學(351100)曾獻峰

縱觀近3年的全國卷,可以發(fā)現(xiàn)曲線的切線問題是高考中的一個高頻考點,例如,2020年I卷第6 題,II卷理科第5題,III卷第10 題;2021年I卷第7 題,II卷第11 題,甲卷理科第13 題,乙卷理科第21 題;2022年I卷第10,11,14,15 題,II卷第14 題,乙卷理科第21 題等.其中一類過點且與函數(shù)相切的直線條數(shù)問題,在求解時往往需要以導數(shù)為工具來研究函數(shù)的性質(zhì)與圖象特征,有較強的綜合性,是培養(yǎng)學生直觀想象,邏輯推理,數(shù)學運算,數(shù)學抽象等數(shù)學核心素養(yǎng)的良好載體,值得一探究竟.

如不作特別說明,下文出現(xiàn)的函數(shù)y=f(x)均是定義域上的二階可導函數(shù),即y=f(x)為凸函數(shù)?f′′(x)≥0;y=f(x)為凹函數(shù)?f′′(x)≤0.

1 凸函數(shù)的切線探究

探究1若定義在R 上的凸函數(shù)y=f(x)有t條漸近線,則過點P(a,b)可作幾條直線與曲線y=f(x)相切?

解析設過點P(a,b)且與曲線y=f(x)相切于點(x0,y0)的切線方程為y=f′(x0)(x - x0)+f(x0), 則b=f′(x0)(a-x0)+f(x0),令F(x)=f′(x)(a-x)+f(x)-b,則可作的切線條數(shù)與函數(shù)y=F(x)的零點個數(shù)相同.F′(x)=f′′(x)(a-x)+f′(x)·(-1)+f′(x)=f′′(x)(a-x),由f′′(x)≥0, 易得當x ＜a時,F′(x)＞0; 當x ＞a時,F′(x)＜0; 所以F(x)在(-∞,a)上單調(diào)遞增, 在(a,+∞)上單調(diào)遞減;F(x)max=F(a)=f(a)-b, 若F(a)＜0 即b ＞f(a),則F(x)無零點,即不存在過(a,b)且與y=f(x)相切的切線;

(1)若t=0,即y=f(x)無漸近線,則當x →±∞,都有f(x)→+∞;所以當x →±∞,F(x)→-∞;若F(a)=0即b=f(a),F(x)恰有1 個零點a,即過(a,b)僅有1 條直線與y=f(x)相切;若F(a)＞0 即b ＜f(a),F(x)有2 個零點,即過(a,b)可作2 條直線與y=f(x)相切;

綜上可得: 如圖1 所示,坐標平面被曲線y=f(x)分割成I,II兩個區(qū)域, 過區(qū)域I內(nèi)的點可作0 條切線; 過區(qū)域II內(nèi)的點可作2 條切線;過曲線上的點僅可作1條切線.

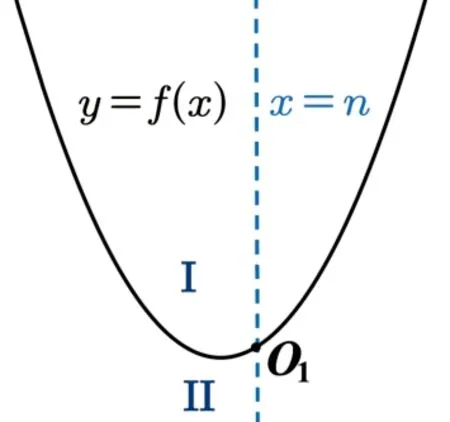
圖1

例如,直線l:x=n交曲線于點O1,則過O1切線僅有1 條,過l上位于O1下方的點可作2 條切線,過O1上方的點的切線不存在.

(2)若t=1,即y=f(x)有一條漸近線,

綜上可得: 如圖2,3 所示,坐標平面被曲線y=f(x)和漸近線y=kx+m分成三個區(qū)域I,II,III,過區(qū)域I內(nèi)的點可作0 條切線;過區(qū)域II內(nèi)的點可作2 條切線,過曲線上的點或漸進線上的點或區(qū)域III內(nèi)的點僅可作1 條切線.例如直線l:x=n交曲線于點O2,交漸近線于O1,則過線段O1O2內(nèi)部的點可作2 條切線,過O1及下方的點僅有1 條切線,過O2僅有1 條切線,過O2上方的點的切線不存在.

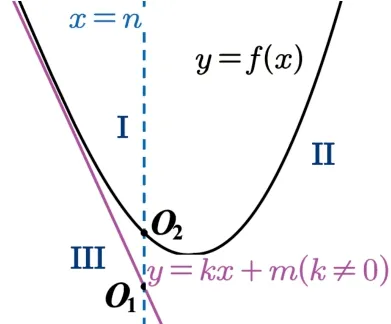
圖2

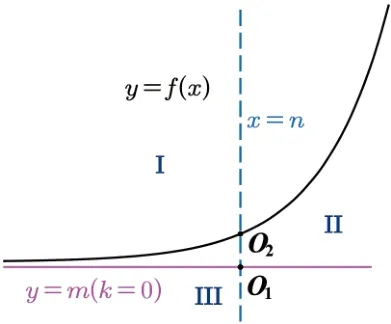
圖3

情況2若f(x)有右漸近線即0,則x →-∞,f(x)→+∞;所以x →-∞,F(x)→+∞;如圖4,5 所示,同理可得,與情況1相同的結論.

圖4

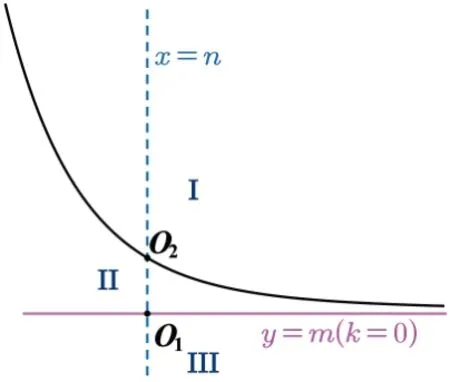
圖5

則F(x)無零點,不存在過(a,b)與y=f(x)相切的直線;

綜上所述,如圖6 所示,曲線y=f(x)及其漸近線將坐標平面分成5 個區(qū)域I,II, III,IV,V, 過區(qū)域I,IV 內(nèi)的點可作0 條切線;過區(qū)域II內(nèi)的點可作2 條切線;過區(qū)域III,V 內(nèi)的點或過曲線上點可作1 條切線; 過兩漸近線交點O可作0 條切線; 過射線OA,OB上的點(不含O)可作1 條切線;過射線OC,OD上的點(不含O)可作0 條切線.例如,直線l:x=n分別交曲線與其漸近線于點O3,O2,O1,則過l上的點O3或線段O2O1(不含O1)上的點僅可作1 條切線;過O3上方或O1下方的點的切線不存在,過線段O2O3(不含端點)上的點的切線有2 條.

圖6

2 凹函數(shù)的切線探究

探究2若定義在R 上的凹函數(shù)y=f(x)有t條漸近線,過點P(a,b)作函數(shù)y=f(x)的切線,可以作幾條?

解析令g(x)=-f(x),則g(x)為凸函數(shù),由探究1 可得類似結論,再將其關于x軸對稱,便可得凹函數(shù)的相關切線結論,此處不再一一羅列.

3 半凸半凹函數(shù)的切線探究

若二階可導函數(shù)y=f(x)滿足f′′(x0)=0 且在x=x0附近兩側f′′(x)異號,稱(x0,f(x0))為函數(shù)y=f(x)的拐點,其圖像特征為y=f(x)在x=x0兩側凹凸性發(fā)生改變.下面對一類半凸半凹函數(shù)的切線問題進行探究.

探究3若函數(shù)y=f(x)有唯一的拐點(x0,f(x0)),過點P(a,b)作函數(shù)y=f(x)的切線,可以作幾條?

解析若f′′(x)從負變化到正, 且f′′(x)僅有一個零點, 即當x ＜x0,f′′(x)＜0;x ＞x0,f′′(x)＞0, 則f(x)在(-∞,x0)上是凹函數(shù),在(x0,+∞)上是凸函數(shù),即函數(shù)y=f(x)先凹后凸(先凸后凹的情況與此類似)

(1)若f(x)無漸近線

同探究1 中解析所示,記F(x)=f′(x)(a-x)+f(x)-b,F′(x)=f′′(x)(a - x), 則F(a)=f(a)- b,F(x0)=f′(x0)(a - x0)+f(x0)- b, 記拐點(x0,f(x0))處的切線方程為g(x)=f′(x0)(x-x0)+f(x0).

①若a=x0,則F′(x)≤0,F(x)在R 上單調(diào)遞減,若F(a)=0 即b=f(a),F(x)有唯一零點x0,則過(x0,f(x0))僅可作1 條切線; 若F(a)＞0,即b ＜f(a),由單調(diào)性可知F(x)在R 上有唯一零點, 即過(x0,b)僅可作1 條切線; 若F(a)＜0,即b ＞f(a),由單調(diào)性可知F(x)在R 上有唯一零點,即過(x0,b)僅可作1 條切線.

②若a ＜x0,則當x ∈(-∞,a)∪(x0,+∞),F′(x)＜0;當x ∈(a,x0),F′(x)＞0; 所以F(x)在(-∞,a)上單調(diào)遞減,在(a,x0)上單調(diào)遞增,在(x0,+∞)上單調(diào)遞減.

③若a ＞x0,同②中的情況一樣分類討論,同理可得類似結論.

綜上,如圖7 所示,坐標平面被曲線y=f(x)和拐點O處的切線分成4 個區(qū)域I,II,III,IV.過區(qū)域I,II內(nèi)的點僅可作1 條切線;過區(qū)域III,IV 內(nèi)的點可作2 條切線;過拐點O可作1 條切線l1;過曲線上的點或切線l1上的點(除拐點O以外)可作2 條切線.例如,直線l:x=n交曲線于點O1,交l1于點O2,則位于線段O1O2內(nèi)部的點可作3 條切線;位于O1上方或O2下方的點可作1 條切線;過O1或O2均可作2條切線.

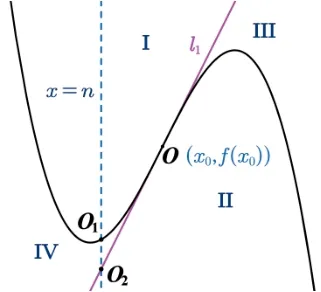
圖7

(2)若y=f(x)有1 條漸近線,類似探究1 以及(1)中的求解過程可得相應的結論,以y=f(x)有一條左漸近線為例,如下結論: 如圖8 所示,坐標平面被曲線y=f(x),拐點O處的切線l拐以及漸近線l漸分成7 塊區(qū)域;過區(qū)域I和VI內(nèi)的點可作3 條切線;過區(qū)域II和VII內(nèi)的點可作2 條切線;過區(qū)域III內(nèi)的點可作0 條切線;過區(qū)域IV 內(nèi)和區(qū)域V 內(nèi)的點可作1 條切線;過拐點O處可作1 條切線;過曲線上除拐點外的點均可作兩條切線;過l拐上O1下方的點(不含O)均可作2 條切線;過l拐上O1及其上方的點可作1 條切線;過l漸上O1左側的點可作2 條切線;過l漸上O1O2段的點(不含端點)可作0 條切線;過l漸上O2右側的點可作2 條切線.

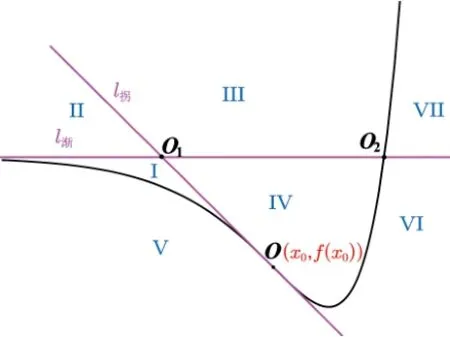
圖8

(3)若y=f(x)有2 條漸近線,此情況較為復雜,有興趣的讀者可自行探究.

評注從圖象上看,具有單個拐點的函數(shù)y=f(x)可以看作是1 個凸函數(shù)和1 個凹函數(shù)通過拐點進行縫合,它們在縫合點處具有相同的切線l,這條切線l將平面分成兩個半平面,一半包含一個凸函數(shù),另一半包含一個凹函數(shù),所以在求解過點P(a,b)的切線問題時,可分別考慮上述兩個半平面內(nèi)的切線條數(shù),再匯總得到整個坐標平面的切線總條數(shù).

4 數(shù)形結合圖解切線條數(shù)問題

例4.1(2021年高考I卷第7 題)若過點(a,b)可以作曲線y=ex的兩條切線,則( )

A.eb ＜aB.ea ＜bC.0＜a ＜ebD.0＜b ＜ea

圖解f(x)=ex,f′′(x)=ex ＞0,所以f(x)為凸函數(shù),且有左漸近線y=0,如圖9 所示,可得當點(a,b)位于區(qū)域II時,過(a,b)可作2 條切線,故選D.

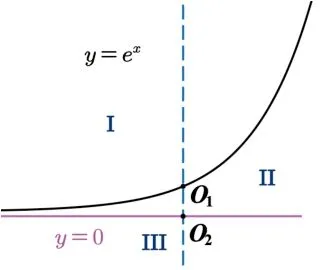
圖9

例4.2(2022年高考I卷第15 題)若曲線y=(x+a)ex有兩條過坐標原點的切線,則實數(shù)a的取值范圍是____.

圖解f(x)=(x+a)ex,f′(x)=(x+a+1)ex,f′′(x)=(x+a+2)ex,所以f(x)有唯一拐點O(-(a+2),-2e-(a+2)),有左漸近線y=0.當x ＜-(a+2),f′′(x)＜0;x ＞-(a+2),f′′(x)＞0, 所以f(x)在(-∞,-(a+2))上是凹函數(shù),在(-(a+2),+∞)上是凸函數(shù).

f(x)在 (-(a+2),-2e-(a+2))處的切線y=-e-(a+2)(x+a+4)交漸近線于點O1(-(a+4),0),如圖10所示,當原點位于O1左側或O2(-a,0)右側時可作2 條切線.所以0＜-(a+4)或-a ＜0,即a ＜-4 或a ＞0.

圖10

例4.3(2014年高考北京卷文科第20 題節(jié)選)已知函數(shù)f(x)=2x3-3x, 若過點P(1,t)存在3 條直線與曲線y=f(x)相切,求t的取值范圍.

圖解f(x)=2x3-3x,f′(x)=6x2-3=3(2x2-1),f′′(x)=12x, 所以y=f(x)有唯 一的拐 點O(0,0), 當x ＜0,f′′(x)＜0;x ＞0,f′′(x)＞0,所以f(x)在(-∞,0)上是凹函數(shù),在(0,+∞)上是凸函數(shù),且無漸近線.

y=f(x)在O(0,0)處的切線方程為y=-3x, 它交x=1 于點O1(1,-3),由圖11 可知,當點P(1,t)位于線段O1O2內(nèi)部時恰有3 條切線,所以-3＜t ＜-1.

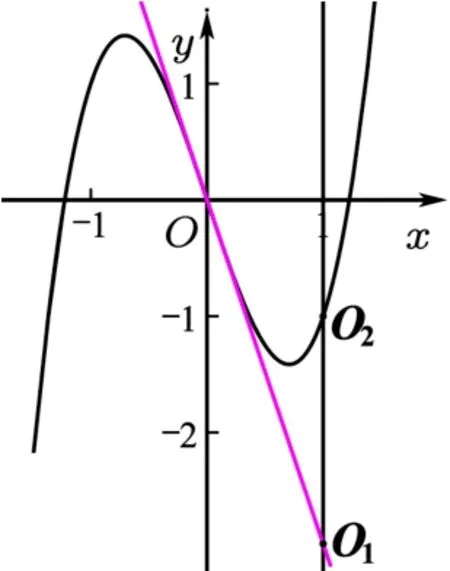
圖11

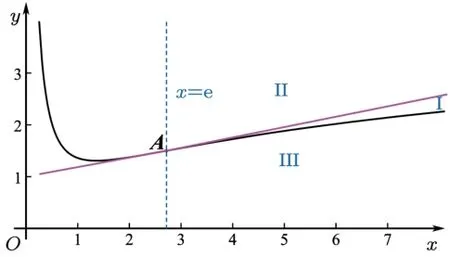
圖12

注本題雖然定義域不為R,但結論依然可用.

5 結束語

過點且與函數(shù)相切的直線條數(shù)與函數(shù)圖象的形態(tài)有著密切的關系,函數(shù)的凹凸性,漸近線以及拐點處的切線是重要的影響因素,如果能把握住函數(shù)的這些要素,看清其幾何背景,對于快速求解此類問題有很大的幫助.