華南師范大學數(shù)學科學學院(510631) 李湖南

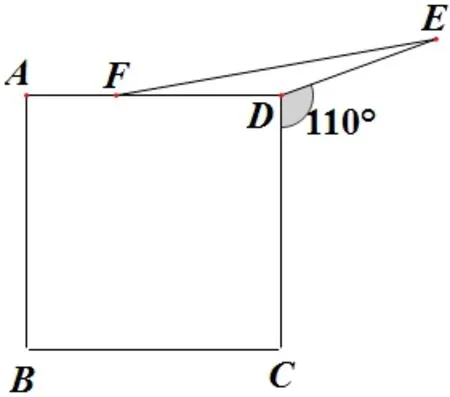
圖1

(A) 160 (B) 164 (C) 166 (D) 170 (E) 174

解 依題意,可得∠FDE=360°-90°-110°=160°,從而∠DFE=∠DEF=10°,故∠AFE=170°,(D)正確.7. 一個學校有100 個學生和5 個老師. 在第一個階段,每個學生只上一門課,每個老師也只教一門課. 所有課程的注冊人數(shù)分別是50,20,20,5,5. 令t是隨機選擇一個老師,他所教課程的注冊人數(shù)的平均值,s是隨機選擇一個學生,他所學課程的注冊人數(shù)(包括他自己)的平均值. 則t-s是多少?

圖2

圖3

圖4

16. 某機關有30 名員工,其中20 名員工使用A型電腦,剩下10 名員工使用B型電腦. 為安全起見,兩臺電腦之間只能使用纜線連接,且纜線僅可以連接一臺A 型電腦和一臺B型電腦. 員工可以彼此交流,如果他們的電腦使用一條纜線連接著或者通過一系列連接的電腦傳送信息. 最初的時候,所有電腦兩兩之間均未連接. 技術員任意選擇每個型號的電腦各一臺并安裝纜線,如果那兩臺電腦尚未連接. 一旦每個員工都可以與其他員工交流,技術員就停止安裝. 問最多可能使用了多少條纜線？

(A) 190 (B) 191 (C) 192 (D) 195 (E) 196

解 如果20 臺A型電腦與10 臺B型電腦均有纜線連接,則有200 條纜線. 原問題等價于最少斷開幾條纜線將導致員工之間不能隨意交流. 很明顯,如果連接一臺指定的A型電腦(比如A1)的10 條纜線都斷開,那么A1 將不能與任何其他員工交流. 此時,還有190 條纜線連接著,只需再任意安裝1 條纜線,就能確保交流通暢. 故最多可能使用了191條纜線,(B)正確.

17. 有多少有序正整數(shù)對(b,c)使得方程x2+bx+c=0和x2+cx+b=0 都沒有兩個不相等的實數(shù)根?

圖5

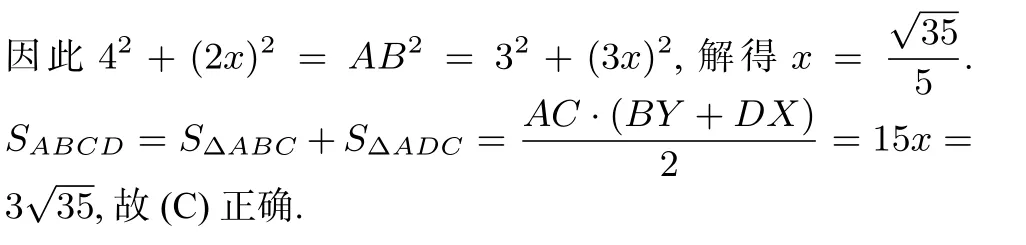
22. 阿扎爾和卡爾玩一字棋. 在3×3 的格子中,阿扎爾先放一個X 在其中一個格子里,接著卡爾在其余格子里放一個O,然后阿扎爾又在其余格子里再放一個X,如此繼續(xù),直到9 個格子全滿了,或者其中一個人先在一行、一列或一條對角線上放了3 個同樣的X 或O,這時候這個人就贏了. 假設兩個人每一步都是隨機下,而不是根據(jù)理性的策略,且卡爾放了第三個O 就贏了. 則游戲結束時的局面有多少種可能?

(A) 36 (B) 112 (C) 120 (D) 148 (E) 160

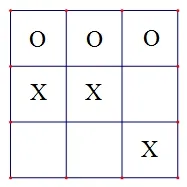
圖6

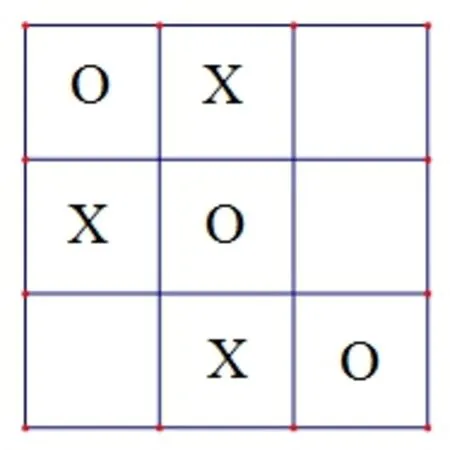
圖7

23. 一個首項系數(shù)為1 的二次實系數(shù)多項式p(x)稱作無禮的(disrespectful),如果方程p(p(x)) = 0 恰好有三個實根. 在所有無禮多項式中,存在唯一一個多項式?p(x)使得其三根之和最大,則?p(1)是多少?

解 設BC=x,CD=y,DA=z,則x,y,z,18 在某種順序下構成等差數(shù)列.若公差為0, 則x=y=z= 18, 此時ABCD是一個菱形,a= 18, 符合要求;若公差不為0, 則x,y,z互異且均小于18, 此時ABCD構成一個梯形. 如圖8 示, 過點D作DE//CB交AB于點E, 則BCDE是一個平行四邊形. 在ΔADE中, 由余弦定理, 可得DE2=AD2+AE2- 2AD · AEcosA,即x2=z2+(18-y)2-z ·(18-y), 化簡得x2+81 =(z-9)2+(y-18)2+yz,分情況討論:

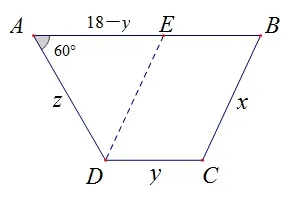
圖8

(1)公差為1:x,y,z ∈{17,16,15},無解; (2)公差為2:x,y,z ∈{16,14,12}, 有一組解x= 14,y= 12,z= 16;(3) 公差為3:x,y,z ∈ {15,12,9}, 無解; (4) 公差為4:x,y,z ∈{14,10,6},無解;(5)公差為5:x,y,z ∈{13,8,3},有一組解x= 13,y= 3,z= 8;顯然,公差不可能大于等于6.

因此,a的所有可能值為3,8,13,12,14,16,18, 其和是84. 故(E)正確.

25. 設m≥5 是個奇數(shù),且m|(a1+a2+a3+a4),其中ai為互異整數(shù)且1 ≤ai≤m,i= 1,2,3,4. 令D(m)表示這樣的四元數(shù)組(a1,a2,a3,a4)的個數(shù),則存在一個多項式q(x) =c3x3+c2x2+c1x+c0使得D(m) =q(m)對所有的奇數(shù)m≥5 成立. 問c1是多少?

(A)-6 (B)-1 (C) 4 (D) 6 (E) 11

解 先考慮ai為互異整數(shù)且1 ≤ai≤m,i= 1,2,3,4的四元數(shù)組(a1,a2,a3,a4),共有m(m-1)(m-2)(m-3)個.