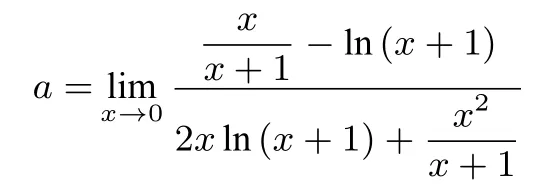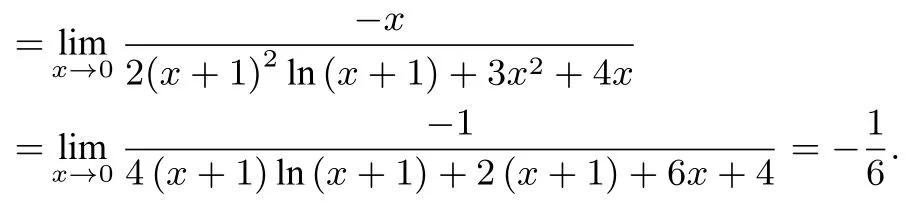已知函數(shù)的極值點求參數(shù)的取值范圍問題的求解策略
廣東省中山市中山紀(jì)念中學(xué)(528454) 李文東
已知x=x0為函數(shù)f(x)的極值點,且f′(x0)=0,求函數(shù)f(x)中的參數(shù)a的取值范圍問題是最近幾年全國和各省市高考的熱點問題,也是難點問題.比如2016年高考山東卷文科第20 題,2018年高考北京卷第19 題以及2018年全國III 卷的導(dǎo)數(shù)壓軸題都對此問題進(jìn)行考查,尤其是全國卷的壓軸題,求解難度非常大,以至于部分教師對標(biāo)準(zhǔn)答案頗感費解.經(jīng)筆者研究,針對此類問題給出常見的求解策略.
策略一:分類討論,考慮函數(shù)的單調(diào)性
例1(2018年高考北京卷第19 題) 設(shè)函數(shù)f(x) =[ax2?(3a+1)x+3a+2]ex.
(Ⅰ)若曲線y=f(x)在點(2,f(2))處的切線斜率為0,求a;
(Ⅱ)若f(x)在x=1 處取得極小值,求a的取值范圍.
解(Ⅰ)略.(Ⅱ)f′(x)=(ax ?1)(x ?1)ex.
(1)當(dāng)a= 0 時,令f′(x) = (1?x)ex,由f′(x) = 0 得x=1.顯然f(x)在(?∞,1)上遞增,在(1,+∞)上遞減,所以f(x)在x=1 處取得極大值,不合題意.
(2)當(dāng)a>0 時,令f′(x)=0 得x1=,x2=1.
①當(dāng)x1=x2,即a=1 時,f′(x)=(x ?1)2ex≤0,所以f(x)在R 上單調(diào)遞增,所以f(x)無極值,不合題意.
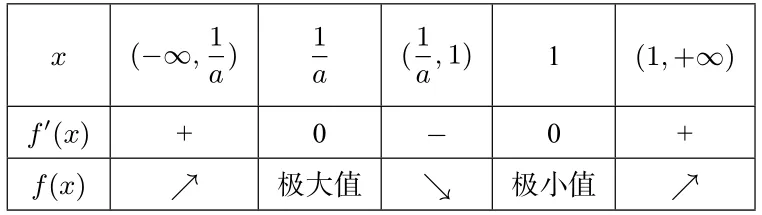
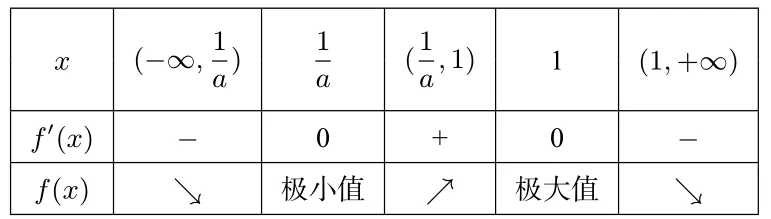
②當(dāng)x1>x2,即0 x (?∞,1)1(1, 1 a)1 a (1 a,+∞)f′(x)+0?0+f(x)↗極大值↘極小值↗ 所以f(x)在x=1 處取得極大值,不合題意. ③當(dāng)x1 x (?∞, 1 a)1 a (1 a,1)1(1,+∞)f′(x)+0?0+f(x)↗極大值↘極小值↗ 所以f(x)在x=1 處取得極小值,即a>1 滿足題意. (3) 當(dāng)a <0 時,令f′(x) = 0 得x1=,x2= 1.f′(x),f(x)如下表: x (?∞, 1 a)1 a (1 a,1)1(1,+∞)f′(x)?0+0?f(x)↘極小值↗極大值↘ 所以f(x)在x=1 處取得極大值,不合題意. 綜上所述,a的取值范圍為(1,+∞). 點評極值點問題其本質(zhì)還是單調(diào)性問題,因此只需要分類討論弄清楚函數(shù)的單調(diào)性即可,這是解決此類問題的一個基本方法.但是,含參函數(shù)單調(diào)性的討論也是導(dǎo)數(shù)中的一個難點問題,因此利用分類討論單調(diào)性來求解此類問題往往比較復(fù)雜. 例2若x=0 是函數(shù)的極大值點,求a的取值范圍. 解 因為x= 0 是f(x) 的極大值點,則存在充分接近于0 的δ >0,使得當(dāng)x ∈(?δ,0) 時,f′(x)>0,當(dāng)x ∈(0,δ) 時,f′(x)<0.分 析f′(x) 的特點可知,當(dāng)x ∈(?δ,0) 時,4a2x2?8ax+ 1?6a >0,當(dāng)x ∈(0,δ)時,4a2x2?8ax+1?6a <0.顯然a= 0 不符合要求; 當(dāng)a ?= 0 時,y= 4a2x2?8ax+1?6a為開口向上的二次函數(shù),則此時它必然經(jīng)過原點,于是1?6a=0,得,于是二次函數(shù)(x ?12),顯然x=0 為f(x)的極大值點.綜上:a的取值范圍為 點評利用極值點的定義,只需要考慮導(dǎo)函數(shù)在極值點附近的符號(局部性質(zhì)),求導(dǎo)后觀察分析導(dǎo)函數(shù)在極值點附近的符號來確定參數(shù)的取值范圍. 例3(2018年高考全國III 卷第21 題) 已知函數(shù)f(x)=(2+x+ax2)ln(x+1)?2x. (1) 若a= 0,證明:當(dāng)?1< x <0 時,f(x)<0; 當(dāng)x>0 時,f(x)>0; (2)若x=0 是f(x)的極大值點,求a. 解(1) 略. (2)f′(x) = (1+2ax)ln(x+1) +?2,則f′(0) = 0,f′′(x) = 2aln(x+1) +則f′′(0) = 0,f′′′(x) =由f′′′(x)=0 得a= 下證:當(dāng)a=時,x= 0 是f(x) 的極大值點.當(dāng)可知f′′(x)在(?1,0)單調(diào)遞增,在(0,+∞)單調(diào)遞減,進(jìn)而有f′′(x)≤f′′(0)=0,從而f′(x)在(?1,+∞)單調(diào)遞減,于是當(dāng)x ∈(?1,0)時,f′(x)> f′(0) = 0,當(dāng)x ∈(0,+∞)時,f′(x)< f′(0) = 0,從而f(x)在(?1,0)單調(diào)遞增,在(0,+∞)單調(diào)遞減,所以x=0 是f(x)的極大值點.綜上:a= 點評極值點的第三充分判別法:已知函數(shù)f(x) 在x=x0處各階導(dǎo)數(shù)都存在,若f′(x0) =f′′(x0) =···=f(n?1)(x0) = 0,f(n)(x0)?= 0,則當(dāng)n為偶數(shù)時,x0是f(x)的極值點(f(n)(x0)>0 為極小值點,f(n)(x0)<0 為極大值點);當(dāng)n為奇數(shù)時,x0不是f(x)的極值點.此種解法借助了高等數(shù)學(xué)中的結(jié)論,已超出了中學(xué)數(shù)學(xué)的知識范疇. 例4題目同例3. 解由題意:x=0 是f(x)的極大值點,則存在充分接近于0 的δ >0,使得當(dāng)x ∈(?δ,0)時,f′(x)>0,當(dāng)x ∈(0,δ)時,f′(x)<0,由于對任意的x ∈(?1,+∞),都有2xln(x+1) ≤0,于是有2xln(x+1)+≤0,分離參數(shù)后有: ①當(dāng)x ∈(0,δ)時,a <②當(dāng)x ∈(?δ,0)時,a >考慮到極值為函數(shù)f(x)在x= 0 處附近的性質(zhì),讓δ →0 并根據(jù)洛必達(dá)法則有: 評注此題難度極高,以至于中學(xué)教師對標(biāo)準(zhǔn)答案也頗感費解,例3 中我們用極值點第三充分判別法解決,但是需要用到較多的高等數(shù)學(xué)知識,這里的解法相對比較簡單,不過也需要用到洛必達(dá)法則,對于相關(guān)知識點需要給學(xué)生補充! 經(jīng)筆者研究,發(fā)現(xiàn)此類問題大部分都可以用分離參數(shù)的方法快速統(tǒng)一解決.其一般模式如下: 以x=x0為函數(shù)f(x)的極小值點為例,且設(shè)f′(x0) =0.根據(jù)極小值點的定義可知:存在充分接近于0 的δ >0,使得當(dāng)x ∈(x0?δ,x0)時,f′(x)<0;當(dāng)x ∈(x0,x0+δ)時,f′(x)>0.假設(shè)f′(x)經(jīng)過變形后得到:當(dāng)x ∈(x0?δ,x0)時,a·g(x) (1) 若當(dāng)x ∈(x0?δ,x0)∪(x0,x0+δ) 時,有g(shù)(x)>0(或g(x)<0),則 當(dāng)x ∈(x0?δ,x0) 時,a <(或a >而 當(dāng)x ∈(x0,x0+δ) 時a >( 或a <由于δ充分小,故此時實數(shù)a的取值范圍為:a= (2)若當(dāng)x ∈(x0?δ,x0)時,有g(shù)(x)>0(或g(x)<0),則而當(dāng)x ∈(x0,x0+δ) 時,g(x)<0(或g(x)>0),則a <由于δ充分小,于是此時實數(shù)a的取值范圍為:a< 例5(2016年高考山東卷文科第20 題) 設(shè)f(x) =xlnx ?ax2+(2a ?1)x,a ∈R. (1)令g(x)=f′(x),求g(x)的單調(diào)區(qū)間; (2)已知f(x)在x= 1 處取得極大值,求實數(shù)a取值范圍. 解(1) 略.(2)f′(x) = lnx ?2ax+ 2a,函數(shù)f(x)在x= 1 處取得極大值,存在充分接近于0 的數(shù)δ >0,使得 當(dāng)x ∈(1?δ,1) 時,f′(x)>0,當(dāng)x ∈(1,1+δ)時,f′(x)<0.分離參數(shù)后可得:當(dāng)x ∈(1?δ,1) 時,; 當(dāng)x ∈(1,1+δ) 時,2a >,從 而即實數(shù)a的取值范圍為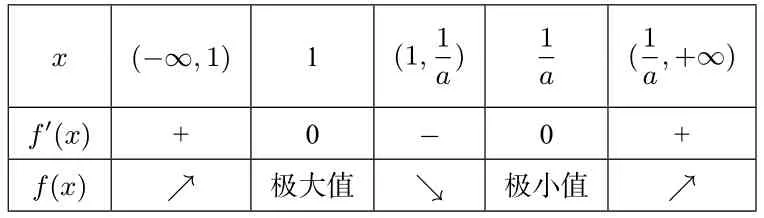
策略二:利用極值點的定義
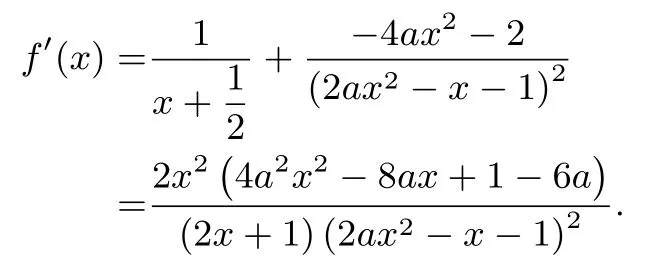
策略三:利用極值點的第三充分判別法
策略四:分離參數(shù)