Hong-Ping Yang(楊宏平), Wen-Juan Yuan(原文娟), Jun Luo(羅俊), and Jing Zhu(朱靜),?

1National Center for Electron Microscopy in Beijing,School of Materials Science and Engineering,the State Key Laboratory of New Ceramics and Fine Processing,Key Laboratory of Advanced Materials(MOE),Tsinghua University,Beijing 100084,China

2Center for Electron Microscopy,Institute for New Energy Materials&Low-Carbon Technologies,School of Materials Science and Engineering,Tianjin University of Technology,Tianjin 300384,China

Keywords: bilayer graphene quantum dots,rotational stacking faults,first-principles calculation

1. Introduction

Graphene has attracted the interest of researchers worldwide due to its unique properties, while numerous experimental and theoretical studies have been conducted on its applications in the fields of electronics,[1]optoelectronics,[2]photonics,[3]photovoltaics,[4]mechanics,[5]quantum interference,[6]quantum computation,[7]field emission,[8]fluorescence emission,[9]and secondary electron emission.[10,11]It has been found that defects such as point defects,[12]line defects,[13]and grain boundaries[14]can modulate the electronic structure and magnetic properties of graphene. Therefore, it is very promising to use defects to modulate the properties of graphene and, thus, develop various functional devices.[15-17]

Rotational stacking faults (RSFs) are a type of intrinsic defects that commonly occur in layered materials, such as folded monolayer and few-layer two-dimensional molybdenum disulfide[18-20]and graphene.[21,22]An RSF refers to the deviation from the standard sequence of the stacking order among layers in a layered material, and a relative rotation exists between the layers. Studies have already shown that RSFs can change the electronic structure of layered materials.[21-24]In particular, bilayer graphene with a small rotation angle,known as the magic angle,has unconventional superconductivity.[25,26]However, the influence of RSFs on the magnetic and electronic properties of bilayer graphene quantum dots has not been fully studied.

In this work,we employed the first-principles calculation based on density functional theory (DFT) to study the electrical and magnetic properties of bilayer graphene quantum dots with RSFs having different rotational angles. Our results show that these bilayer graphene quantum dots have different magnetic moments, energy levels, and spin distributions.For example, some graphene quantum dots have spin up in both highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital(LUMO),while some have spin down and up. These results indicated that RSFs with different rotational angles can be used to modulate the magnetism and electronic structures of bilayer graphene quantum dots,aiding us to develop various new electronic,magnetic,and spintronic devices.

2. Calculation methodology

The software used in this study for the first-principles calculation was the Vienna ab initio simulation package(VASP).[27]The methodology used was the projector augmented wave(PAW)[28]method.The exchange correlation energy was evaluated using the Perdew-Burke-Ernzerhof(PBE)formulation,[29]a derivation of the generalized gradient approximation. The cutoff kinetic energy of the plane wave basis set was set at 400 eV. The convergence threshold energy was set to 10-5eV.The supercell used in the calculation had a vacuum layer of at least 20 ?A in all three directions which was large enough to avoid interactions between adjacent bilayer graphene quantum dots. Therefore,only a k-point was used to express the Brillouin zone. To determine the ground states of the bilayer graphene quantum dots, the spin polarization and non-spin polarization of all models were also determined. The total energy was compared,and the lower energy state was selected as the ground state for the following calculation.

3. Results and discussion

Because many RSF rotational angles were found in the experiments,[18-21,30,31]we selected bilayer graphene quantum dots with RSF angles of 0°,8.95°,19.11°,30°,40.89°,51.05°,and 60°as examples for calculations. The total number of atoms was 138,which was the same as that in a previous work on molybdenum disulfide quantum dots.[32]Among them,the bilayer graphene quantum dots with the 60°RSFs were actually in the most stable AB stacking form. Figure 1(a)-1(n)show three-dimensional(3D)views and top views of bilayer graphene quantum dots with RSF rotational angles of 0°,8.95°,19.11°,30°,40.89°,51.05°,and 60°,respectively. For convenience, we label these models as configurations A, B,C, D, E, F, and AB, respectively. Figure 2 shows the relaxed structures of these models. From Figs. 1 and 2, we find that the model structures of configurations A-F prior to and after relaxation were not the same, and the models after relaxation did not become the most stable AB stacking form,which indicate that the emergence of RSFs is ubiquitous. The unrelaxed models can be considered as partial and restricted structures that were extracted from an infinite bilayer graphene. Thus,to comprehensively study the magnetic and electronic structural properties of bilayer graphene quantum dots with RSFs,we performed DFT calculations for both the unrelaxed and relaxed models.

We first performed calculations for the unrelaxed models. The total energy differences between the spin polarized state and the non-spin polarized state of the seven models in Fig. 1 were -1.5 eV, -3.8 eV, -3.2 eV, -5.5 eV, -2.4 eV,-0.3 eV, and -5.9 eV, respectively. The total energies of all the spin polarized states were lower, which indicates that the ground states of these models were all magnetic.[15,33]Their magnetic moments were 28.0001μB, 21.2795μB, 20.2941μB,15.8469μB, 21.9491μB, 19.8623μB, and 28.0067μB, respectively,where μBdenotes the Bohr magneton. Figure 3 shows the spatial distribution of unpaired spins of the seven unrelaxed models. They were mainly concentrated at the edge of the models,which indicates that magnetism mainly originated from the edge structure of the models.

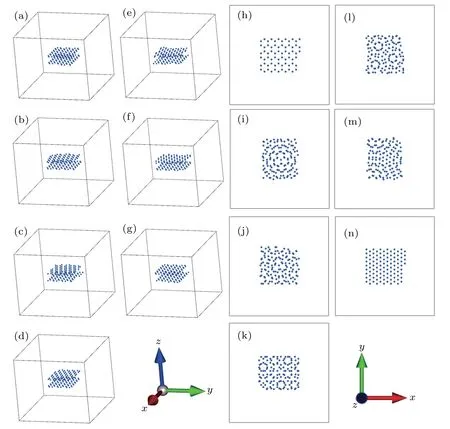
Fig.1. Unrelaxed model of bilayer graphene quantum dots with seven different RSF rotational angles: (a)0°,(b)8.95°,(c)19.11°,(d)30°,(e)40.89°,(f)51.05°,and(g)60°.These models are labeled as configurations A,B,C,D,E,F,and AB,respectively.(h)-(n)The corresponding top views of(a)-(g).

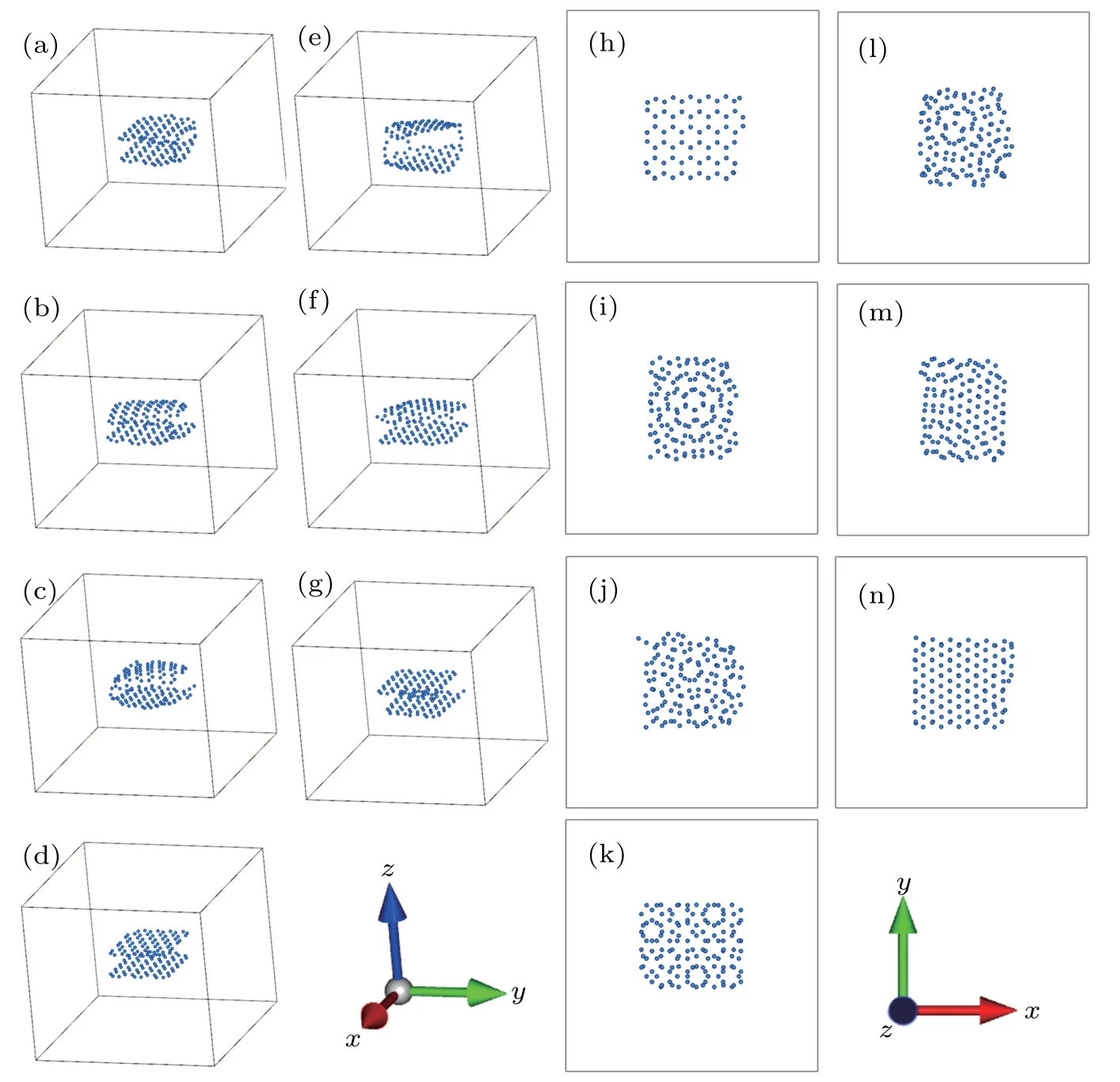
Fig.2. Relaxed model of bilayer graphene quantum dots with seven different RSF rotational angles: (a)0°,(b)8.95°,(c)19.11°,(d)30°,(e)40.89°,(f)51.05°,and(g)60°. (h)-(n)The corresponding top views of(a)-(g).

Fig.3.Spatial distribution of unpaired spins of the unrelaxed bilayer graphene quantum dots models with seven different RSF rotational angles.Unpaired spins were obtained by subtracting the spin down density from the spin up density;results in positive values are shown in light blue,and results in negative values are shown in light yellow. (a)-(g)The 3D views and(h)-(n)the top views of(a)-(g),respectively.

Figure 4 shows the energy level structure and spin state near the Fermi level of the seven unrelaxed models. Because the ground states were all spin polarized,their electronic structures also split into two states. We then define the majority spins and minority spins as spin up and spin down, respectively. The energy level structure and the spin distribution were also different for these models.Among them,the HOMO and LUMO of models A, B, and C were both spin up, those of models D,E,and AB were spin up and spin down,respectively,and the HOMO and LUMO of model F were spin down and spin up, respectively. This indicates that different RSF rotational angles could be used to modulate the spin distribution of bilayer graphene, thereby obtaining different spin polarized currents,which is critical for the production of spintronic devices.[34]A comparison of Figs. 1, 3, and 4 shows that the difference in the magnetic moment and spin distribution originated from the different stacking modes of the bilayer graphene,namely,the difference in the rotational angles.

In addition, we also observed that the LUMO-HOMO energy gaps of these seven models varied in magnitude, and were 0.0009 eV(0°),0.0128 eV(8.95°),0.0094 eV(19.11°),0.0108 eV(30°),0.0028 eV(40.89°),0.0044 eV(51.05°),and 0.0271 eV(60°),respectively. These differences implied that the electron conduction of these seven quantum dots showed different responses to an external electric field. Their ability to generate photons and interact with photons also differed.[35]This is advantageous for designing and producing various allcarbon electronic and optoelectronic functional devices.

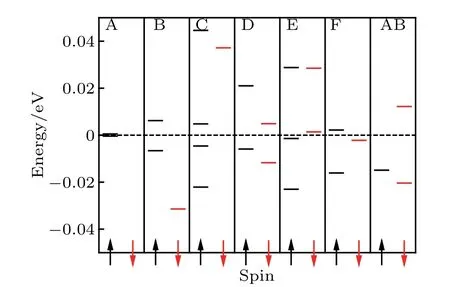
Fig.4. Distribution of the energy levels near the Fermi level of the unrelaxed models of bilayer graphene quantum dots with different RSF rotational angles. Labels A-F and AB correspond to models A-F and AB, respectively. The dashed line represents the Fermi level. The energy levels in black and red correspond to spin up and spin down, respectively.

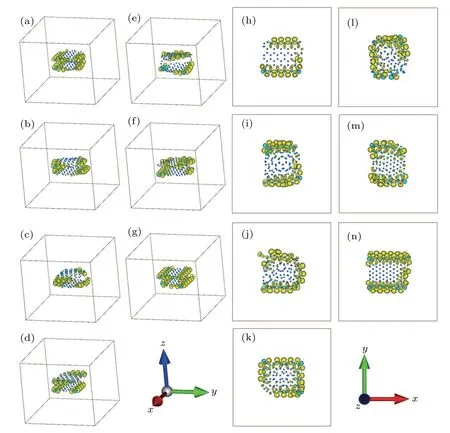
Fig.5. Spatial distribution of unpaired spins of the relaxed bilayer graphene quantum dots models with seven different RSF rotational angles.Unpaired spins were obtained by subtracting the spin down density from the spin up density;results in positive values are shown in light blue,and results in negative values are shown in light yellow. (a)-(g)The 3D views and(h)-(n)the top views of(a)-(g),respectively.

We then performed DFT calculations for the relaxed models and found that the results were very similar to those of the unrelaxed models, as shown in Figs. 5 and 6. The total energy differences between the spin polarized state and the non-spin polarized state of these models were -5.7 eV,-3.8 eV,-4.1 eV,-4.3 eV,-4.4 eV,-3.5 eV,and-6.5 eV respectively, which indicates that the ground states of these models were all magnetic. The spatial distributions of unpaired spins of these models showed that the magnetism also mainly originated from the edge structure of the models. As shown in Fig. 5, the magnetic moments were 20.0000μB,16.2101μB, 16.0000μB, 18.0000μB, 14.0000μB, 16.0000μB,and 26.0000μB,respectively.The energy gaps of these relaxed models were 0.0870 eV, 0.0282 eV, 0.0665 eV, 0.2408 eV,0.3059 eV, 0.3068 eV, and 0.2907 eV, respectively. Similar to the DFT results of the unrelaxed models, the energy levels and spin distributions of the relaxed models also varied with changes in the RSF rotational angles,as shown in Fig.6.Figures 3 and 5 show that the magnetic moment of bilayer graphene quantum dots mainly originated from the edge, regardless of relaxation. Different rotational angles led to different edge structures, resulting in different magnetic moments.Thus, different RSF rotational angles can modulate the magnetic moment of bilayer graphene quantum dots. The DFT results in Figs. 4 and 6 demonstrated that RSFs of different rotational angles can modulate the distribution of spin and energy level of bilayer graphene quantum dots,regardless of relaxation.

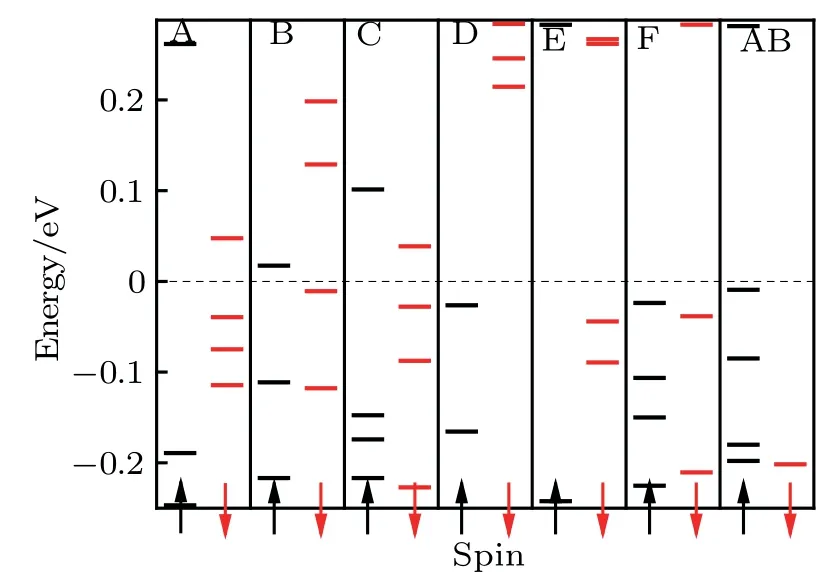
Fig.6. Distribution of energy levels near the Fermi level of the relaxed models of bilayer graphene quantum dots with different RSF rotational angles.Labels A-F and AB correspond to models A-F and AB,respectively. The dashed line represents the Fermi level. The energy levels in black and red correspond to spin up and spin down,respectively.

To better understand the effect of different RSF rotational angles on the magnetic moment and energy gap of bilayer graphene quantum dots,we plotted the magnetic moment and energy gap of unrelaxed and relaxed models together as a function of the rotational angle,as shown in Fig.7. The maximum magnetic moments of both unrelaxed and relaxed models were found to occur around 0°and 60°. The minimum values occurred around 30°and 51°for the unrelaxed models,and 19°and 41°for the relaxed models,as shown in Fig.7(a). This indicates that RSFs with different rotational angles can modulate the magnetism of bilayer graphene quantum dots. Figure 7(b)shows that the maximum energy gap of the unrelaxed model corresponded to around 9°and 60°, and the minimum value corresponded to around 0°and 41°.The maximum energy gap of the relaxed model corresponded to around 0°and 41°,and the minimum value corresponded to around 9°and 60°. The trends for the maximum and minimum energy gaps of the two models were the exact opposite,indicating that the restrictiveness at the edge of the quantum dots had a significant influence on the properties of the electronic structure,thus further confirming that RSFs with different rotational angles can modulate the electronic structure of bilayer graphene quantum dots,regardless of relaxation. Therefore,bilayer graphene quantum dots with RSFs having different rotational angles are a potential means to tailor the properties of graphene. This can be used to develop different electronic,magnetic,and spintronic devices based on bilayer graphene quantum dots.

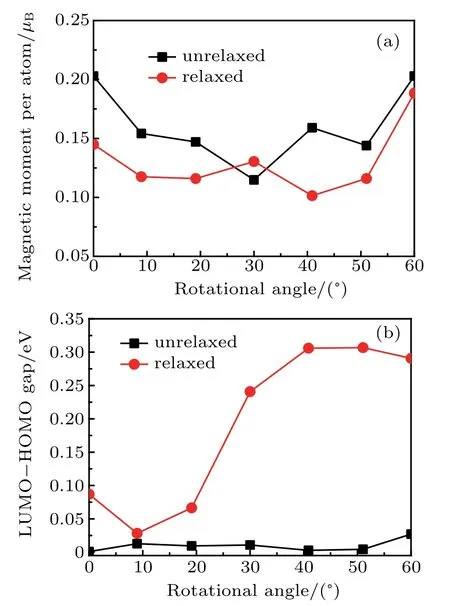
Fig. 7. (a) Plot of magnetic moment against rotational angle for unrelaxed and relaxed models of bilayer graphene quantum dots with different RSF rotational angles. (b) Plot of LUMO-HOMO energy gap against rotational angle for unrelaxed and relaxed models of bilayer graphene quantum dots with different RSF rotational angles.

To explore the source of the magnetic moments of these models,we focused on the bilayer graphene quantum dots with a 30°RSF rotational angle as an example and determined the magnetic moment of each atom in the quantum dots by using Bader charge analysis.[36-38]Figure 8 shows the magnetic moment of individual atoms in the unrelaxed bilayer graphene quantum dots. We added the magnetic moments of each atom to obtain a sum of 15.8467μB, this is consistent with the total magnetic moment in the DFT calculation;i.e.,15.8469μB.This demonstrates the validity of the Bader charge analysis.Figure 9 shows the results of the relaxed model. The sum of the magnetic moments of the individual atoms was 18.0000μB,consistent with the total magnetic moment in the DFT calculation;i.e.,18.0000μB. Figures 8 and 9 show that atoms with larger magnetic moments were all near the edge, while the magnetic moments of the inner atoms were much smaller.This finding suggests that the magnetic properties of these models originate mainly from their edge atoms, which is consistent with our conclusions from the spatial distributions of unpaired spins in Figs.3 and 5,and the results of other works.[32,33,39,40]Because the magnetic moments of bilayer graphene quantum dots are mainly derived from the edge atoms,and the number of edge atoms is proportional to the quantum dot size,the number of total atoms is proportional to the square of the quantum dot size, the maximum magnetic moments of the edge atoms are all about 1μB,as shown in Figs.8 and 9,so it can be concluded that the average atomic magnetic moments of quantum dots decrease with the increase of the size, which is similar to the nanoribbons.[33]In addition,we also found that the distribution of the magnetic moment of each atom in the relaxed quantum dot model was more stable than the unrelaxed model,where atoms with negative magnetic moment essentially disappeared and the magnetic moments were more concentrated at the edge.

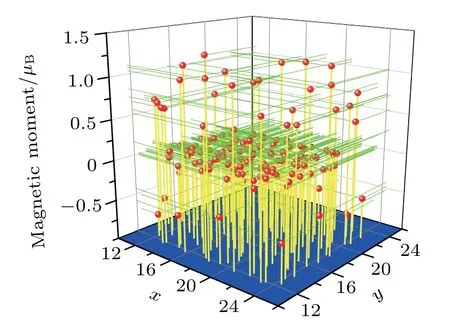
Fig. 8. Magnetic moment of individual atom obtained through the Bader charge analysis of unrelaxed bilayer graphene quantum dots with 30° RSF rotational angle.

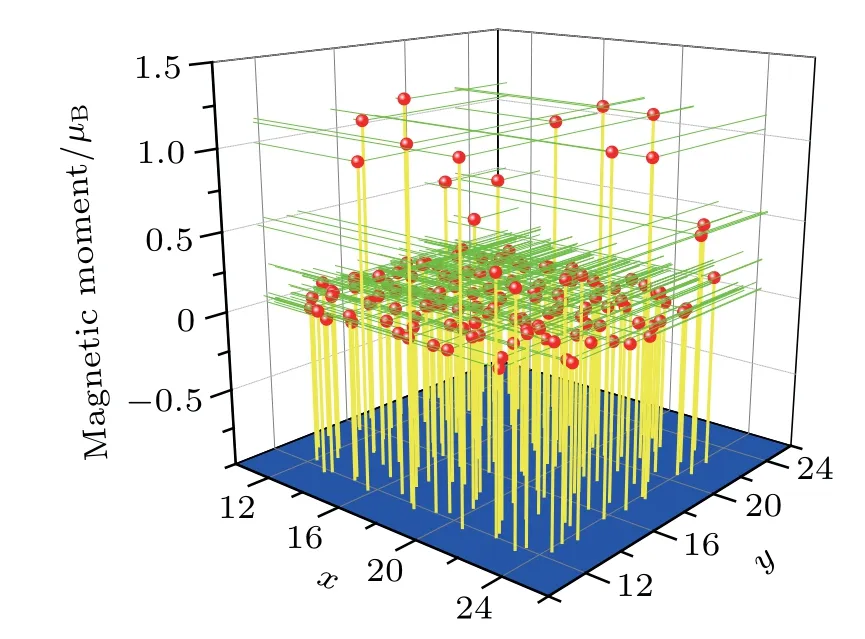
Fig. 9. Magnetic moment of individual atom obtained through the Bader charge analysis of relaxed bilayer graphene quantum dots with 30° RSF rotational angle.

4. Conclusion

Our first-principles calculation results show that bilayer graphene quantum dots containing RSFs with different rotational angles are all magnetic, while the magnetic moment varies with changes in the rotational angles. By examining the spatial distribution of unpaired spins and through Bader charge analysis,we confirm that the magnetic moment mainly originates from the edge atoms,while the rotational angle determines the edge structure. Consequently, we can modulate the magnetic moment of bilayer graphene quantum dots using RSFs with different rotational angles. We also discover that RSFs with different rotational angles can modulate the distribution of energy level and spin of bilayer graphene quantum dots. We expect that our findings will potentially open a new path of defect engineering to produce electronic, magnetic,and spintronic devices with a variety of functions.