湖北省武漢職業(yè)技術(shù)學(xué)院商學(xué)院(430074) 鄒 峰

文[1]中給出一類雙對(duì)稱二元二次方程式的最值問題的解法,筆者就這一問題深入研究,給出特定的二元二次方程式的約束下,巧用三角換元,求函數(shù)f(x,y)的最值,給出其統(tǒng)一解法,下面給出四類函數(shù)f(x,y)的表達(dá)式應(yīng)用舉例,然后給出幾個(gè)推論和一個(gè)推廣.

下文的特定約束條件是指：實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,其中a,c∈R+,b∈R且2a＞b.以下,我們考慮在如上的特定約束條件下,求函數(shù)f(x,y)的最值,且f(x,y)是常見的二元一次或二元二次多項(xiàng)式等.

由ax2+bxy+ay2=c,考慮待定系數(shù)k1,k2∈R+,滿足k1(x+y)2+k2(x-y)2=c,可得(k1+k2)x2+2(k1-k2)xy+(k1+k2)y2=c,即解得整理可得可設(shè)θ∈R解得令于是可設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,其中λ1,λ2∈R+,代入方程ax2+bxy+ay2=c,可得然后代入f(x,y)進(jìn)行求最值,筆者視為統(tǒng)一解法.

第一類若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,b≠0),求函數(shù)f(x,y)=x2+y2的最大值M和最小值m.

例1(2016年河北高中數(shù)學(xué)預(yù)賽第7題)已知實(shí)數(shù)x,y滿足x2+xy+y2=3,則x2+y2的取值范圍.

解設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得λ1=1,則所以x2+y2=2cos2θ+6sin2θ=2(1+2sin2θ)∈[2,6].

例2已知實(shí)數(shù)x,y滿足2x2-3xy+2y2=3,則x2+y2的最大值M和最小值m.

解設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得則故當(dāng)θ=0時(shí),M=6,當(dāng)

推論若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b),則x2+y2的最大值M和最小值m.當(dāng)b＞0時(shí),當(dāng)b＜0時(shí),

第二類若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,b≠0),求函數(shù)f(x,y)=ax2-bxy+ay2的最大值M和最小值m,稱為一類雙對(duì)稱二元二次方程式的最值問題.

例3已知實(shí)數(shù)x,y滿足x2-xy+y2=1,求x2+xy+y2的最大值M和最小值m.

解設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得則故x2+xy+y2=當(dāng)θ=0時(shí),M=3,當(dāng)

例4已知實(shí)數(shù)x,y滿足3x2-5xy+3y2=10,求3x2+5xy+3y2的最大值M和最小值m.

解設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得則故當(dāng)θ=0時(shí),M=110,當(dāng)

推論若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b),則ax2-bxy+ay2的最大值M和最小值m.當(dāng)b＞0時(shí),當(dāng)b＜0時(shí),

第三類若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函數(shù)f(x,y)=rx2+sxy+ty2的最大值M和最小值m.

例5已知實(shí)數(shù)x,y滿足x2+xy+y2=1,

(1)求x2+2xy+3y2的最大值M和最小值m.

(2)求x2-2xy-3y2的最大值M和最小值m.

解(1)設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,由統(tǒng)一解法可得則故

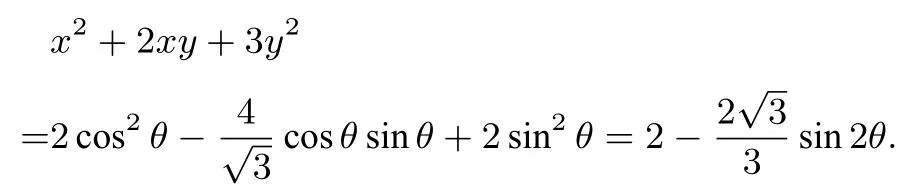
當(dāng)sin2θ=-1時(shí),當(dāng)sin2θ= 1時(shí),

(2)λ1=λ2=1,則x=+sinθ,y=故x2-2xy-3y2=當(dāng)sin(2θ+φ)=1時(shí),當(dāng)sin(2θ+φ)=-1時(shí),

推論1 若實(shí)數(shù)x,y滿足x2+xy+y2=1,則rx2+sxy+ty2的最大值M和最小值m分別為

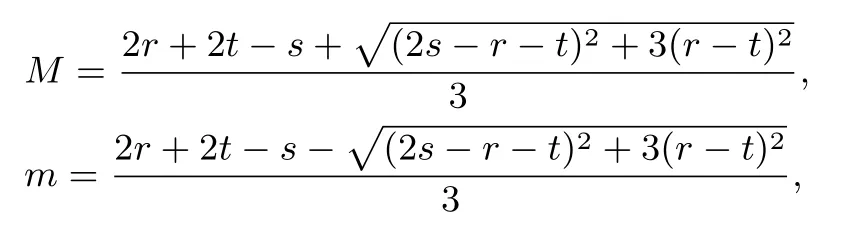
其中r,s,t∈R,且滿足若r=t=1時(shí),s≠1;若r=t=0時(shí),s∈R,若s=0,r與t都不為0.

推論2若實(shí)數(shù)x,y滿足x2-xy+y2=1,則rx2+sxy+ty2的最大值M和最小值m分別為

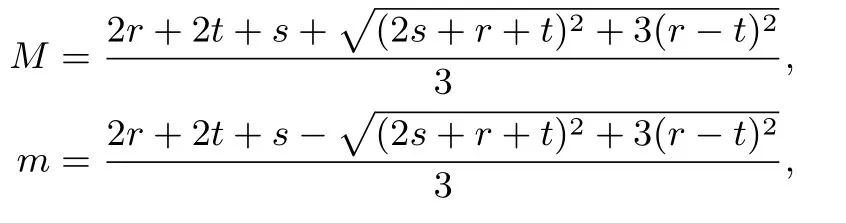
其中r,s,t∈R,且滿足若r=t=1時(shí),s≠-1;若r=t=0時(shí),s∈R,若s=0,r與t都不為0.

例6 已知實(shí)數(shù)x,y滿足2x2+xy+2y2=5,求3x2+2xy+y2的最大值M和最小值m.

解設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得λ1=1,則故

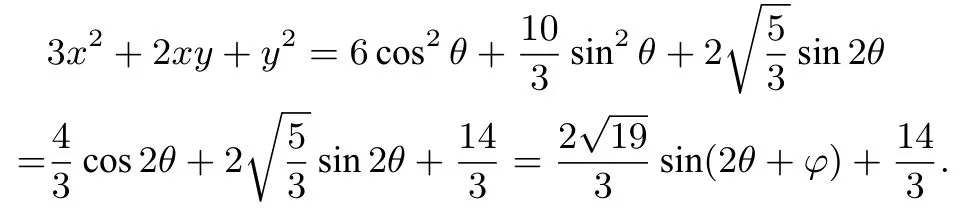
當(dāng)sin(2θ+φ)=1時(shí),當(dāng)sin(2θ+φ)=-1時(shí),

推廣若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b),則rx2+sxy+ty2的最大值M和最小值m分別為

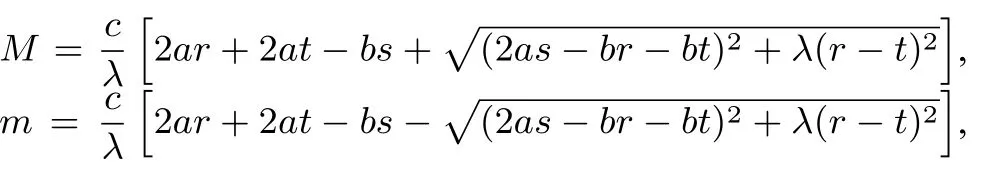
其中λ=(2a+b)(2a-b),r,s,t∈R,且滿足若a=r=t時(shí),b≠s;若r=t=0時(shí),s∈R;若s=0,r與t都不為0.

第四類若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函數(shù)f(x,y)=r(x+y)3+s(x+y)2+t(x+y)+w的最大值M和最小值m.

例7已知實(shí)數(shù)x,y滿足x2+xy+y2=6,求x2y+xy2-x2-2xy-y2+x+y的最大值M和最小值m.

解設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得則由x2+xy+y2=6得xy=(x+y)2-6,故x2y+xy2-x2-2xy-y2+x+y=xy(x+y)-(x+y)2+x+y=[(x+y)2-6](x+y)-(x+y)2+x+y=(x+y)3-(x+y)2-5(x+y).令f(t)=t3-t2-5t,f′(t)= 3t2-2t-5= 0,得

第四類問題解題思路如下：

若實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函數(shù)f(x,y)=r(x+y)3+s(x+y)2+t(x+y)+w的最大值M和最小值m.其中r,s,t∈R,且滿足r,s,t至多有二個(gè)為0.

第一步,設(shè)x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由統(tǒng)一解法可得則

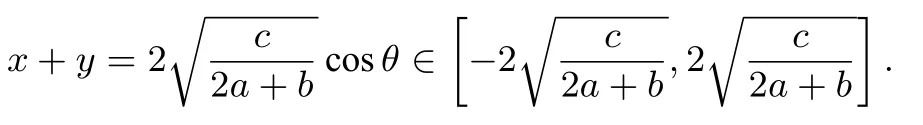
第二步,令

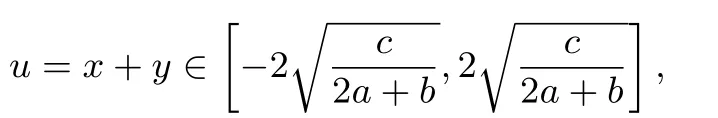
則f(u)=ru3+su2+tu+w,求導(dǎo)f′(u)=3ru2+2su+t=0,在命題的過程中,考慮s2≥3rt及然后求其最值.

練習(xí)

(1)已知實(shí)數(shù)x,y滿足2x2+xy+2y2=5,求-3x2+2xy-y2的最大值M和最小值m.

(2)已知實(shí)數(shù)x,y滿足求f(x,y)=的最大值M和最小值m.

總結(jié)上述同一條件已知實(shí)數(shù)x,y滿足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函數(shù)f(x,y)的最值,函數(shù)f(x,y)的表達(dá)式舉不勝數(shù),關(guān)于其它函數(shù)f(x,y)的表達(dá)式最值問題下文再研究.