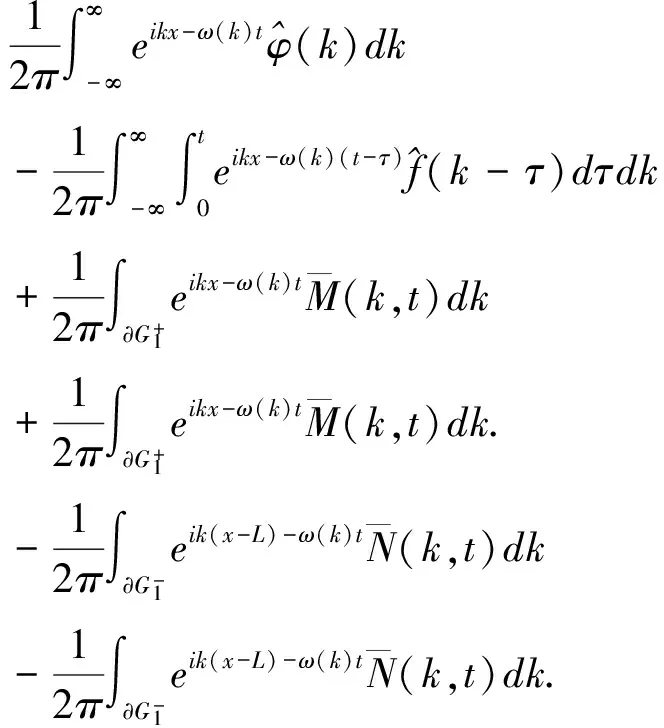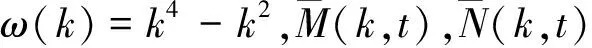一類有限區(qū)間上Kuramoto Sivashinsky方程的初邊值問題
王宏偉,賀怡婷,楊彩鳳,宗 慧
(安陽師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院 河南 安陽455000)
1 引言
Kuramoto[1]在研究三維反應(yīng)擴(kuò)散系統(tǒng)的角相位湍流時(shí),導(dǎo)出了如下一類四階非線性方程
ut+uxxxx+uxx+uux=0
(1)
同時(shí), Sivashinsky[2]在研究二維空間微熱擴(kuò)散不穩(wěn)定性問題時(shí)也導(dǎo)出了相同的數(shù)學(xué)模型. 因此, 方程(1)被稱為KS方程. 該方程Cauchy問題的研究, 已有很多結(jié)論[3,4]. 本文將在有限區(qū)間[0,L]上研究如下一類線性KS方程的初邊值問題
{ut+uxxxx+uxx=f,0≤x≤L,t≥0
u(0)=φ(x),
u(0,t)=g0(t),ux(0,t)=g1(t),
u(L,t)=h0(t),u(L,t)=h1(t)
(2)
根據(jù)近年來由Fokas[5-7]創(chuàng)立的UTM方法, 我們給出這個(gè)方程的一個(gè)顯式解公式, 該公式將為這類方程適定性問題和數(shù)值計(jì)算的研究提供新的研究思路.
2 顯式解的推導(dǎo)過程
利用Fourier變換易知, 方程(1)的象征是ω(k)=k4-k2.假設(shè)e-ikx+ω(k)tu是方程(2)的一個(gè)解, 則
(e-ikx+ω(k)tu)t=e-ikx+ω(k)tf-[e-ikx+ω(k)t(uxxx+ikuxx-(k2-1)ux-(ik3-ik)u)]x.
在區(qū)域D={0≤x≤L,0 ?D(e-ikx+ω(k)tu)tdtdx- ?D[e-ikx+ω(k)tfdtdx =-?D[e-ikx+ω(k)t(uxx+ikuxx-(k2-1)ux-(ik3 -ik)u)]xdtdx. 使用格林公式, 有 -(ik3-ik)u)dt 即 -1)ux(0,s)-(ik3-ik)u(0,s))dt -1)ux(L,s)-(ik3-ik)u(0,s))dt 定義空間變量在區(qū)間[0,L]上的函數(shù)u(x,t)的Fourier變換為 另外, 記 則下列等式成立 =-m3(ω(k),T)-ikm2(ω(k),T)+(k2-1)m1(ω(k),T)+(ik3-ik)m0(ω(k),T) +eikL[n3(ω(k),T)+ikn2(ω(k),T)-(k2-1)n1(ω(k),T)-(ik3-ik)n0(ω(k),T)] 將上式中的T替換為t, 并令 M(k,t)=m3(ω,t)+ikm2(ω,t)-(k2-1)m1(ω,t)-(ik3-ik)m0(ω,t), (3) N(k,t)=n3(ω,t)+ikn2(ω,t)-(k2-1)n1(ω,t)-(ik3-ik)n0(ω,t). (4) 則有 (5) 根據(jù)方程(2)的初始條件和邊界條件, 在(5)式中, 只有m3,m2,n3,n2是未知項(xiàng), 其他各項(xiàng)均可以用已知條件來表示. 下面我們來計(jì)算m3,m2,n3,n2. 解方程λ4-λ2=k4-k2,有四個(gè)根, 分別是 將λj(j=1,2,3,4)依次替換(5)中的k, 令 得到方程組 {m3+iλ1m2-e-iλ1L[n3+iλ1n2]=μ1, m3+iλ2m2-e-iλ2L[n3+iλ2n2]=μ2, m3+iλ3m2-e-iλ3L[n3+iλ3n2]=μ3, m3+iλ4m2-e-iλ4L[n3+iλ4n2]=μ4. 解這個(gè)方程組, 得到 其中 在復(fù)平面上定義區(qū)域G={k|Re(ω(k))<0}, 如果k=x+yi,則區(qū)域G可以表示為 {(x,y)|x4-6x2y2+y4-x2+y2<0}. (6) 由復(fù)變函數(shù)中的Cauchy定理知, (7) (8) 就可以得到本文的主要結(jié)論. 定理1 初邊值解問題(1)的顯式解是 [參考文獻(xiàn)] [1]KURAMOTO Y, TSUZUKI T. On the formation of dissipative structures in reaction-diffusion systems[J]. Theor. Phys, 1975, 54: 687-699. [2]SIVASHINSKY G I. Nonlinear analysis of hydrodynamic instability in laminar flames-I Derivation of basic equations[J]. Acta Astronaut, 1977, 4: 1177-1206. [3]TADMOR E. The well-posedness of the Kuramoto Sivashinsky equation[J]. SIAM J. Math. Anal, 1986, 17:884-893. [4]COLLET P, ECKMANN J P, EPSTEIN H, STUBBE J. A global attracting set for the Kuramoto Sivashinsky equation[J]. Comm. Math. Phys, 1993, 152: 203-214. [5]FOKAS A S. A unified transform method for solving linear and certain nonlinear PDEs[J]. Proc. Roy. Soc. London Ser. A, 1997, 453: 1411-1443. [6]HIMONAS A A, MANTZAVINOS D. The “good”Boussinesq equation on the half-line[J]. J. Differential Equations, 2015, 258(9): 3107-3160. [7]FOKAS A S. HIMONAS A A, MANTZAVINOS D, The Korteweg de Vries equation on the half-line[J]. Nonlinearity, 2016, 29(2): 489-527.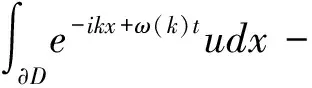
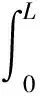
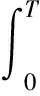
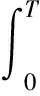
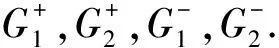
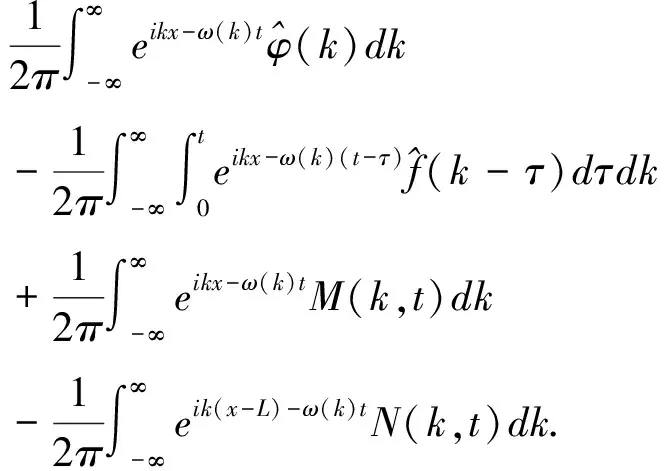

3 結(jié)論