時(shí)統(tǒng)業(yè)

(海軍指揮學(xué)院 信息系,南京 211800)

對(duì)數(shù)η-凸函數(shù)的積分不等式

時(shí)統(tǒng)業(yè)

(海軍指揮學(xué)院 信息系,南京 211800)

對(duì)數(shù)η-凸函數(shù)是對(duì)數(shù)凸函數(shù)的推廣,對(duì)數(shù)η-凸函數(shù)積分不等式的研究可以從對(duì)數(shù)凸函數(shù)積分不等式的研究中得到啟示.從對(duì)數(shù)η-凸函數(shù)的定義出發(fā),結(jié)合一些分析技巧,建立了涉及對(duì)數(shù)η-凸函數(shù)的積分不等式,得到其算術(shù)平均值的上下界.在特殊情況下得到對(duì)數(shù)凸函數(shù)的Hermite-Hadamard型不等式.

對(duì)數(shù)η-凸函數(shù); 對(duì)數(shù)凸函數(shù); 積分不等式

Abstract: Log-η-convex functions are the generalization of log-convex functions.The study of integral inequalities for log-η-convex functions can be inspired from the study of integral inequalities for log-convex functions.Based on the definition of log-η-convex functions and using some analytic skills,the integral inequalities are established,and the upper and lower bounds of the arithmetic mean involving log-η-convex functions are obtained.In particular cases,Hermite-Hadamard type inequalities for log-convex functions are obtained.

Key words: log-η-convex function,log-convex function,integral inequality

0 引言

作為通常凸函數(shù)的推廣,文[1]引入-凸函數(shù)的概念．

定義1[1]設(shè)區(qū)間I??,二元函數(shù)η:?×?→?,f:I→?,若對(duì)任意x,y∈I,t∈[0,1]有

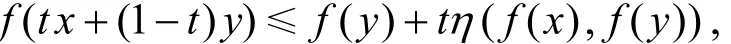
則稱f是區(qū)間I上的-凸函數(shù)．

引理1[2]若f:[a,b]→?是-凸函數(shù)且在(a,b)內(nèi)可微,則對(duì)任意x∈[a,b],y∈(a,b),有

當(dāng)η(x,y)=x-y時(shí),-凸函數(shù)即為通常的凸函數(shù)．有關(guān)-凸函數(shù)的性質(zhì)可見文[1～4]．文[2]給出了如下-凸函數(shù)的Hermite-Hadamard型不等式:

對(duì)數(shù)凸函數(shù)[5]是凸函數(shù)的推廣．文[6]給出了如下對(duì)數(shù)凸函數(shù)的Hermite-Hadamard型不等式:

其中第二個(gè)、第三個(gè)和第四個(gè)不等式的成立與f(x)的凸性沒有關(guān)系,L[f(a),f(b)]是f(a)與f(b)的對(duì)數(shù)平均,即

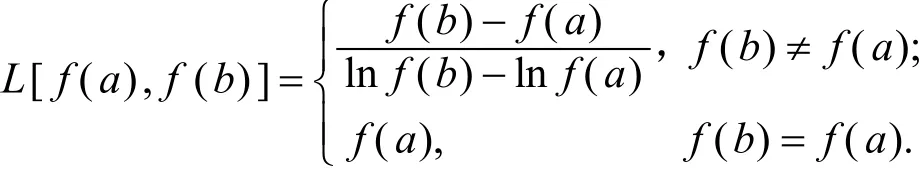
定義2[7]設(shè)f:I→(0,+∞),η:lnf(I)×lnf(I)→?．若對(duì)任意x,y∈I,t∈[0,1]有

則稱f是對(duì)數(shù)-凸函數(shù)．

在定義2中取t=1,可知對(duì)任意x,y∈I有η(lnf(x),lnf(y))≥lnf(x)-lnf(y),從而對(duì)任意x,y∈I有

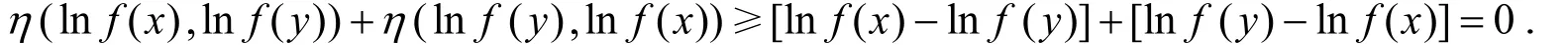
為方便起見,記η(lnf;a,b)=η(lnf(a),lnf(b))+η(lnf(b),lnf(a))．

顯然f是對(duì)數(shù)-凸函數(shù)當(dāng)且僅當(dāng)lnf是-凸函數(shù)．若對(duì)任意x,y∈I,都有η(lnf(x),lnf(y))=lnf(x)-lnf(y),則對(duì)數(shù)-凸函數(shù)即為對(duì)數(shù)凸函數(shù)．若f:[a,b]→?是-凸函數(shù),在lnf([a,b])×lnf([a,b])上有上界,則f在[a,b]上可積[6]．易知,若在lnf([a,b])×lnf([a,b])上小于等于0,則f在[a,b]上恒為常數(shù),且對(duì)任意x,y∈[a,b],有η(lnf(x),lnf(y))=0．

1 主要結(jié)果

定理1 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),在lnf([a,b])×lnf([a,b])上有上界,則有

推論1 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),正數(shù)Mη是在lnf([a,b])×lnf([a,b])上的上界,則有

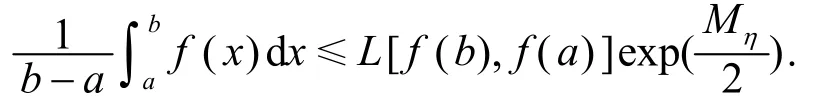
注1 若對(duì)任意x,y∈[a,b],都有η(lnf(x),lnf(y))=lnf(x)-lnf(y),則對(duì)數(shù)-凸函數(shù)即為對(duì)數(shù)凸函數(shù),此時(shí)式(1)即為引言中提到的對(duì)數(shù)凸函數(shù)的Hermite-Hadamard型不等式．

定理2 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),且在lnf([a,b])×lnf([a,b])上有上界,則有

推論2 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),正數(shù)Mη是在lnf([a,b])×lnf([a,b])上的上界,則有

證明由于在(0,+∞)上單調(diào)增加,且,再利用定理2即可．

定理3 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),在lnf([a,b])×lnf([a,b])上有上界,且

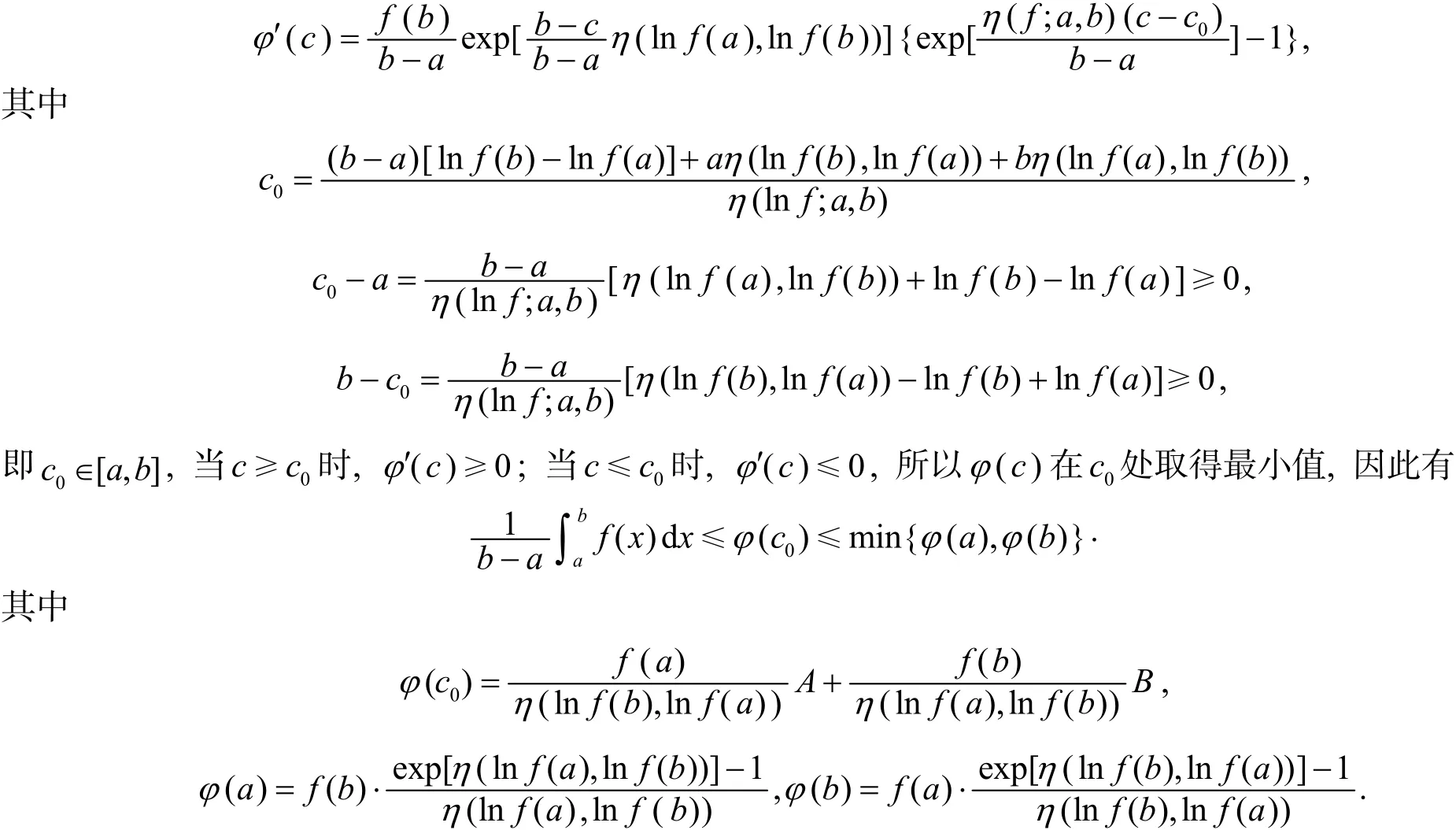
定理4 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),正數(shù)Mη是在lnf([a,b])×lnf([a,b])上的上界,則有

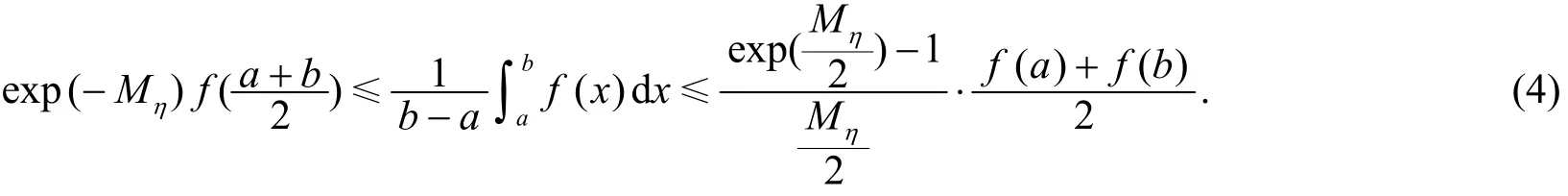
定理5 設(shè)f是[a,b]上的對(duì)數(shù)-凸函數(shù),f在點(diǎn)處可導(dǎo),且,在lnf([a,b])×lnf([a,b])有上界,則有

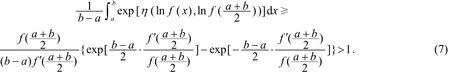
注2 若對(duì)任意x,y∈[a,b],都有η(lnf(x),lnf(y))=η(lnf(x)-lnf(y)),則對(duì)數(shù)-凸函數(shù)即對(duì)數(shù)凸函數(shù),此時(shí)由定理5可得

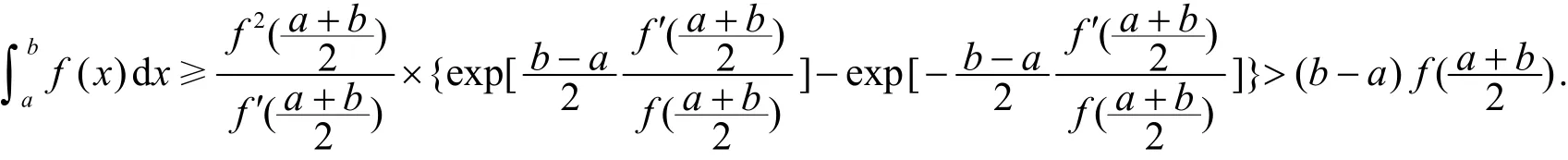
這是文[8]給出的對(duì)數(shù)凸函數(shù)的一個(gè)結(jié)果．

[1]Gordji M E,Delavar M R,De La Sen M.Onφ-convex functions[J].J.Math.Inequal.,2016,10(1): 173～183

[2]Delavar M R,Dragomir S S.On η-convexity[J].Math.Inequal.Appl.,2017,20(1): 203～216

[3]Gordji M E,Dragomir S S,Delavar M R.An inequality related toη-convex functions(II)[J].Int J Nonlinear Anal Appl,2015,6(2): 26～32

[4]Delavar M R,Sen M.Some generalizations of Hermite-Hadamard type inequalities[J].SpringerPlus,2016,1(5): 1～9

[5]吳善和.對(duì)數(shù)凸函數(shù)與琴生型不等式[J].高等數(shù)學(xué)研究,2004,7(5): 61～64

[6]Dragomir S S,Mond B.Integral inequalities of Hadamard type for log-convex functions[J].Demonstratio Math.,1998,31 (2): 354～364

[7]Delavar M R,Sajadian F.Hermite-Hadamard type integral inequalities for log-η-convex functions[J].Mathematics and Computer Science,2016,1(4):86～92

[8]張小明,褚玉明.解析不等式新論[M].哈爾濱: 哈爾濱工業(yè)大學(xué)出版社,2011: 181～184

Integral Inequalities for Log-η-Convex Functions

SHI Tongye
(Department of Information,PLA Naval Command College,Nanjing 211800,China)

O178; O174.13

A

1672-5298(2017)03-0001-05

2017-06-14

時(shí)統(tǒng)業(yè)(1963?),男,河北張家口人,碩士,海軍指揮學(xué)院信息系副教授.主要研究方向: 基礎(chǔ)數(shù)學(xué)