北京師范大學(xué)出版集團(tuán)(100875) 岳昌慶

一類三角函數(shù)值域的統(tǒng)一解法

北京師范大學(xué)出版集團(tuán)(100875) 岳昌慶

形如的值域問(wèn)題在高中階段的不同時(shí)期會(huì)以不同的面貌出現(xiàn),可以轉(zhuǎn)化為圓的參數(shù)方程及切線問(wèn)題統(tǒng)一求解．

一類三角函數(shù)值域 統(tǒng)一解法 圓的參數(shù)方程

高中學(xué)習(xí)過(guò)程中,會(huì)多次遇到形如

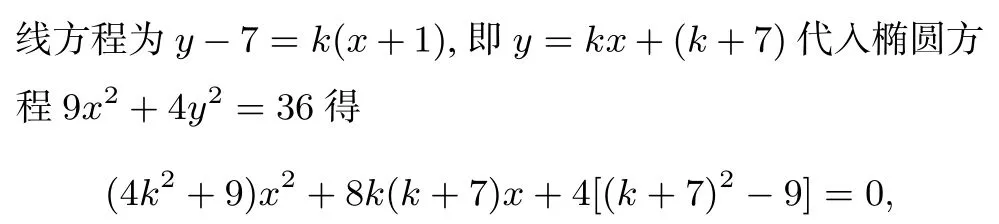
考慮上式的判別式Δ=0,經(jīng)整理可得

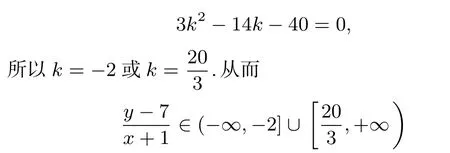
評(píng)注圓錐曲線的切線問(wèn)題似有超綱之嫌,但在學(xué)習(xí)“導(dǎo)數(shù)與微分”知識(shí)之后,就正常多了．

第3次是在學(xué)習(xí)圓錐曲線參數(shù)方程相關(guān)知識(shí)后,仍以例1為例,

評(píng)注(1)也有教師用橢圓的參數(shù)方程轉(zhuǎn)化為例2來(lái)做,但對(duì)于文科的學(xué)生來(lái)講,略顯超綱．

(2)本質(zhì)上,上述例1、例2是同一個(gè)題目,上述三種解法均是例1的不同解法．

由解法3可得:

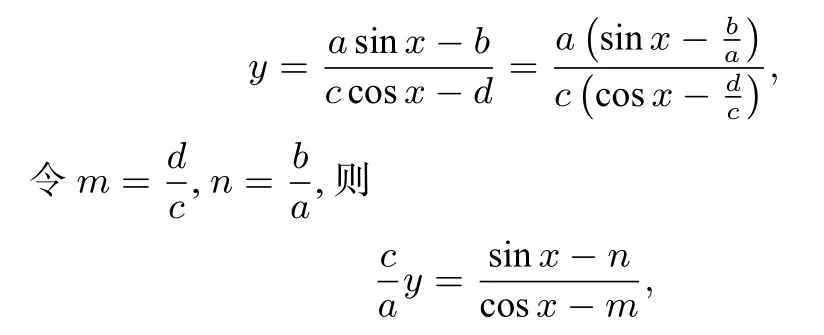
所以求

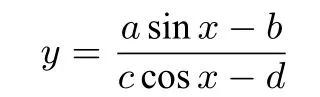
的值域問(wèn)題可以轉(zhuǎn)化為求

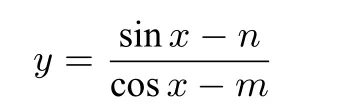
的值域,進(jìn)一步可以轉(zhuǎn)化為單位圓x2+y2=1及一點(diǎn)Q(m,n),向單位圓上任一點(diǎn)所作直線的斜率的取值范圍．

(1)若m2+n2＜1,則Q(m,n)在單位圓內(nèi),較平凡．

(2)若m2+n2＞1,則Q(m,n)在單位圓外,不妨設(shè)Q(m,n)向單位圓所作的切線的斜率為k1,k2,且k1＜k2,