李彥君,楊勝良

(蘭州理工大學(xué)理學(xué)院,甘肅 蘭州 730050)

加權(quán)Motzkin序列的Hankel行列式

李彥君,楊勝良

(蘭州理工大學(xué)理學(xué)院,甘肅 蘭州 730050)

基于經(jīng)典的Motzkin路引入了一類新的加權(quán)Motzkin路的定義,用這種路給出了一類指數(shù)型Riordan矩陣的組合解釋,得到了相應(yīng)的Riordan矩陣第0列元素(加權(quán)Motzkin序列)的加法公式.作為應(yīng)用,得到了一類加權(quán)Motzkin序列的Hankel行列式的計(jì)算方法.

指數(shù)型Riordan矩陣;加權(quán)Motzkin路;加法公式;Hankel行列式

1 引言

2 指數(shù)型Riordan矩陣的組合解釋及加法公式

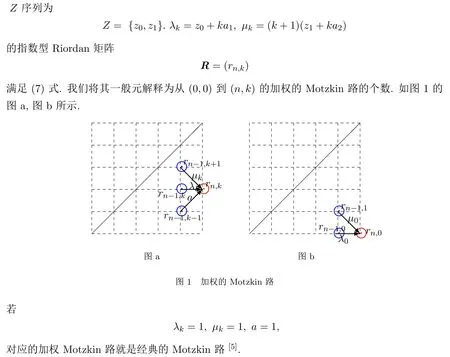
定理2.1一個(gè)Z序列為{z0,z1},A序列為{a,a1,a2}的指數(shù)型Riordan矩陣R=(rn,k)滿足加法公式:

其中

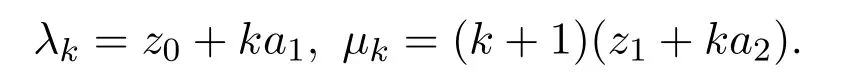
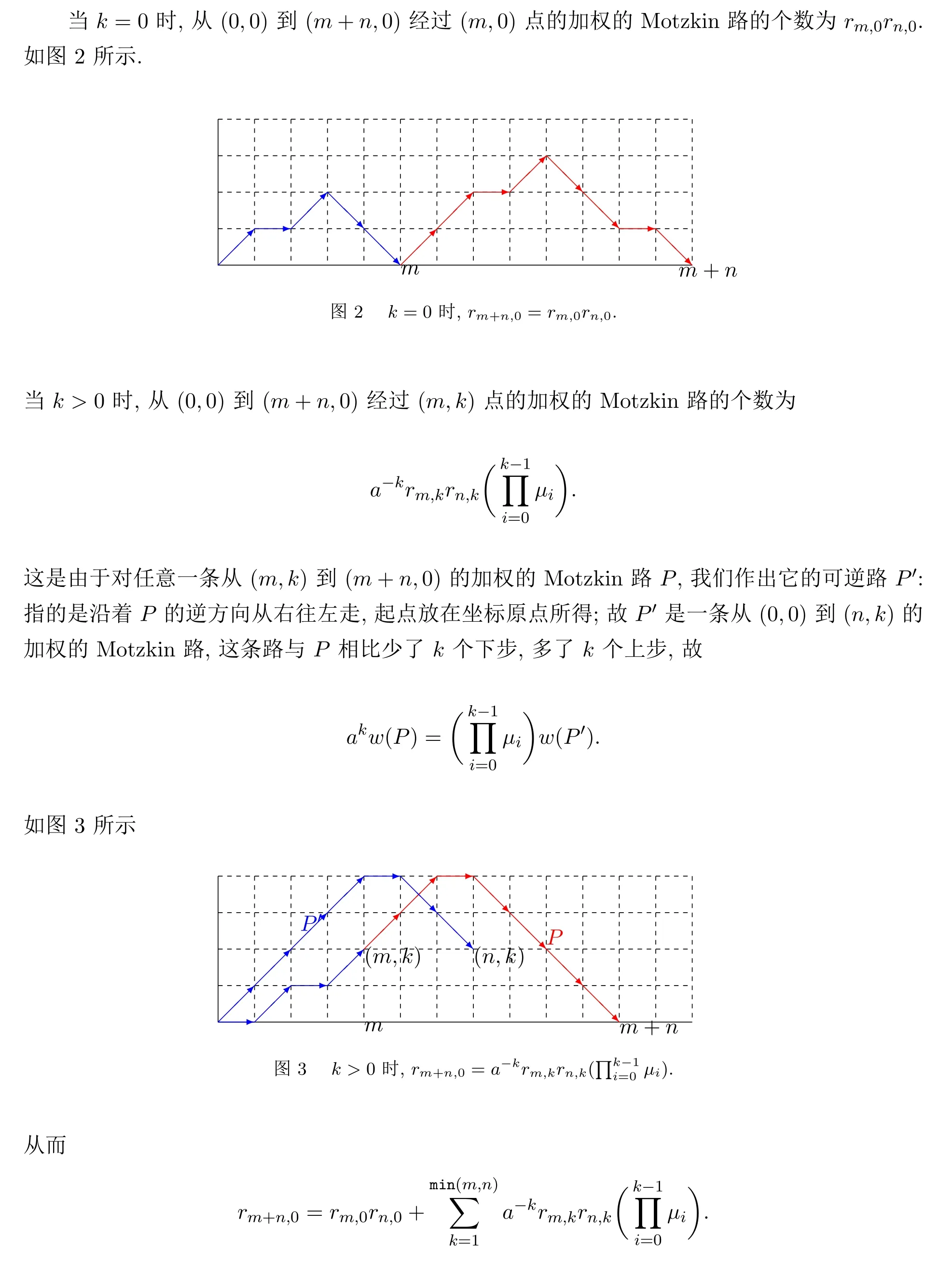
3 加權(quán)Motzkin序列的Hankel行列式及其應(yīng)用

設(shè)(rn)n≥0是一個(gè)實(shí)數(shù)序列,由序列(rn)n≥0所確定的n階Hankel矩陣[6-7]

將Z序列為{z0,z1},A序列為{a,a1,a2}的指數(shù)型Riordan矩陣[g(t),f(t)]的第0列元素(rn,0=n![tn]g(t))稱為加權(quán)的Motzkin序列,記作序列(rn)n≥0.

定理 3.1加權(quán)Motzkin序列(rn)n≥0的Hankel矩陣的行列式為:

這里λk=z0+ka1,μk=(k+1)(z1+ka2).

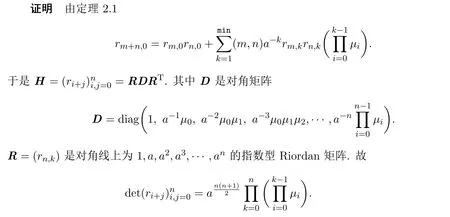
注3.1若a=1,則有

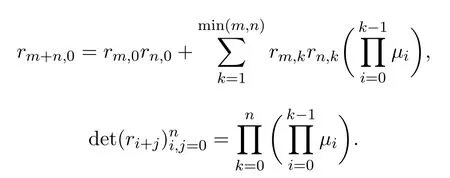
這是文獻(xiàn)[5]的結(jié)果,在文獻(xiàn)[5]中是用歸納法進(jìn)行證明的,這里我們將其結(jié)果推廣并且給出了格路證明.

注3.2當(dāng)x=1時(shí)就是Bell序列A000110(文獻(xiàn)[10])的Hankel行列式,對于x=1的情況在文獻(xiàn)[11]中用類似的方法做的,這里我們將其做到多項(xiàng)式序列上去,使得應(yīng)用更加廣泛.

注3.3該例題的指數(shù)型Riordan矩陣對角線上的元素不全為1,是定理2.1和定理3.1的一個(gè)典型應(yīng)用.在文獻(xiàn)[5-11]中,有相似的結(jié)果.我們得到的得結(jié)果相對于文獻(xiàn)[5-11]有以下優(yōu)勢：

1.本文的結(jié)論是建立在定理2.1和定理3.1基礎(chǔ)上的,定理2.1有嚴(yán)格的組合證明,有一定的組合意義,而文獻(xiàn)[5-11]是在歸納法的基礎(chǔ)上得到的.顯然我們的結(jié)論更有實(shí)際意義.

2.本文得到的結(jié)論比文獻(xiàn)[5-11]要廣,文獻(xiàn)[5-11]中僅僅考慮了指數(shù)型矩陣對角線上的元素全為1的情況,顯然更加廣泛.

3.對于同樣一個(gè)Hankel矩陣,能得到不同的分解,最后得到相同的結(jié)論,比如該例題中由階乘數(shù)序列構(gòu)成的Hankel矩陣還可以有下面不同的分解.

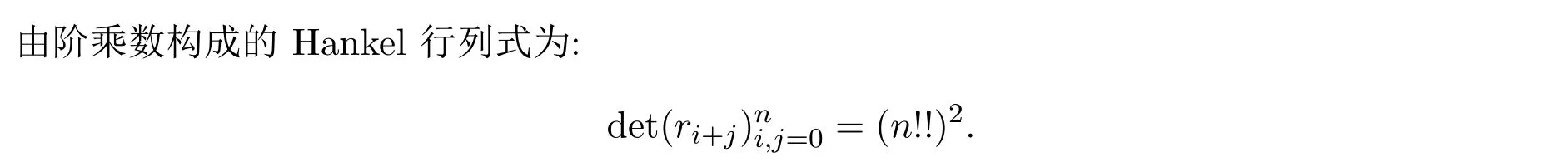
注 3.4該例題中對a取不同的值就會(huì)得到由階乘數(shù)序列構(gòu)成的Hankel矩陣的不同的分解,最后得到一致的結(jié)論.前三個(gè)例題得到的是多項(xiàng)式序列的Hankel行列式,本文對其中的x取特殊的值，就能得到許多的Hankel行列式的值,這在其他文獻(xiàn)中是沒有的.最后兩個(gè)例題是指數(shù)型Riordan矩陣對角線上元素不全為1的具體的例子,能夠具體的反映定理2.1和定理3.1的結(jié)果.

[1]Shapiro L W,Getu S,Woan W J,et al.The Riordan group[J].Discrete Applied Mathematics,1991, 34(1/3):229-239.

[2]Barry P.Constructing Exponential Riordan arrays from their A and Z sequences[J].Journal of Integer Sequences,2014,17:1-19.

[3]Deutsch E,Ferrari L,Rinaldi S.Production matrices and Riordan array[J].Annals of Combinatorics,2009,13: 65-85.

[4]Deutsch E,Ferrari L,Rinaldi S.Production matrices[J].Adv.in Appl.Math.,2005,34:101-122.

[5]Peart P,Woan W J.Generating functions via Hankel and Stieltjes matrices[J].Journal of Integer Sequences, 2000,3(2):Article 00.2.1.

[6]Aigner M.Motzkin numbers[J].European J.of Comb.,1998,19:663-675.

[7]Aigner M.Catalan-like numbers and determinants[J].J.Combin.Theory Ser,1999,87(A):33-51.

[8]Barry P.Riordan arrays,Orthogonal polynomials as moments and Hankel transforms[J].Journal of Integer Sequences,2011,14:1-37.

[9]Sivasubramanian S.Hankel determinants of some sequences of polynomials[J].Seminaire Lotharingien de Combinatoire,2010,63:1-8.

[10]Sloane N J A.The On-Line Encyclopedia of Integer Sequences[OL].published electronically at http://oeis.org,2014.

[11]Aigner M.A characterization of the Bell numbers[J].Discrete Math.,1999,205:207-210.

[12]王麗娟,楊勝良.Riordan矩陣在廣義Motzkin路計(jì)數(shù)中的應(yīng)用[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2016,32(2):160-168.

The Hankel determinants of some weighted Motzkin sequences

Li Yanjun,Yang Shengliang
(School of Science,Lanzhou University of Technology,Lanzhou 730050,China)

Based on the classical Motzkin paths,a new family of weighted Motzkin paths is introduced.By means of those paths,the combinatorial interpretation of some Exponential Riordan arrays are given.Meanwhile, the addition formula of the 0 column elements of Riordan arrays,i.e.,weighted Motzkin sequences,is obtained.As an application,the evaluation of Hankel determinants of some weighted Motzkin sequences are also obtained.

exponential Riordan array,weighted Motzkin path,addition formula,Hankel determinant

O157.1

A

1008-5513(2017)01-0026-11

10.3969/j.issn.1008-5513.2017.01.004

2016-10-16.

國家自然科學(xué)基金(11561044).

李彥君(1990-),碩士生,研究方向：代數(shù)組合與組合優(yōu)化.

2010 MSC:05A15,15A09.