劉威,套格圖桑

(內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,內(nèi)蒙古 呼和浩特 010022)

(2+1)維耗散長波方程的新精確解及其局域激發(fā)

劉威,套格圖桑

(內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,內(nèi)蒙古 呼和浩特 010022)

用改進(jìn)的雙曲正切函數(shù)展開法,獲得了(2+1)維耗散長波方程的由指數(shù)函數(shù)分別與三角函數(shù)和雙曲函數(shù)組合的復(fù)合型新解.復(fù)合型新解中含有關(guān)于變量的任意函數(shù).根據(jù)函數(shù)的任意性,借助符號(hào)計(jì)算系統(tǒng)Mathematica對(duì)解進(jìn)行數(shù)值模擬,可以得到豐富的局域激發(fā)和分形結(jié)構(gòu).

改進(jìn)的雙曲正切函數(shù)展開法;(2+1)維耗散長波方程;局域激發(fā);復(fù)合型解

1 引言

尋找非線性偏微分方程的求解方法與解釋解的性質(zhì)是孤立子與可積系統(tǒng)理論的重要研究內(nèi)容之一.隨著計(jì)算機(jī)技術(shù)的發(fā)展,提出了求解非線性發(fā)展方程的輔助方程法,如齊次平衡法和tanh函數(shù)展開法等.1997年,李提出了tanh函數(shù)展開法[1],該方法可以有效地求出一些方程的解[2-5].本文改進(jìn)了雙曲正切函數(shù)展開法[6],得到了(2+1)維耗散長波方程的含有y為變量的任意函數(shù)的復(fù)合型新解.文獻(xiàn)[6]得到的解是本文給出的復(fù)合型解的特殊情況.根據(jù)函數(shù)的任意性,選取適當(dāng)?shù)暮瘮?shù),可以得到(2+1)維耗散長波方程的局域激發(fā)和分形結(jié)構(gòu).

2 (2+1)維耗散長波方程的簡化

文獻(xiàn)[6]中依齊次平衡法的基本思想,設(shè)(2+1)維耗散長波方程

的解為

其中

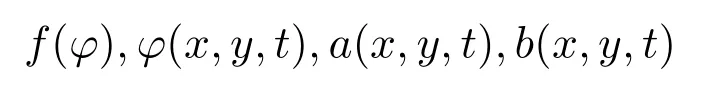
為待定函數(shù),λ為待定常數(shù).

利用函數(shù)u(x,y,t)和η(x,y,t)間的變換關(guān)系η=λuy+b?λay,可將方程(1),(2)的求解問題轉(zhuǎn)化為Burgers方程

的求解問題.將(3)式代入(5)式進(jìn)一步整理后令的f′,f′,f0系數(shù)為零,可得如下約束條件

若選取a(x,y,t)=c(y),則(6)-(8)式化為如下約束條件

3 (2+1)維耗散長波方程的新解

文獻(xiàn)[6]中假設(shè)(9)式,(10)式的解為:

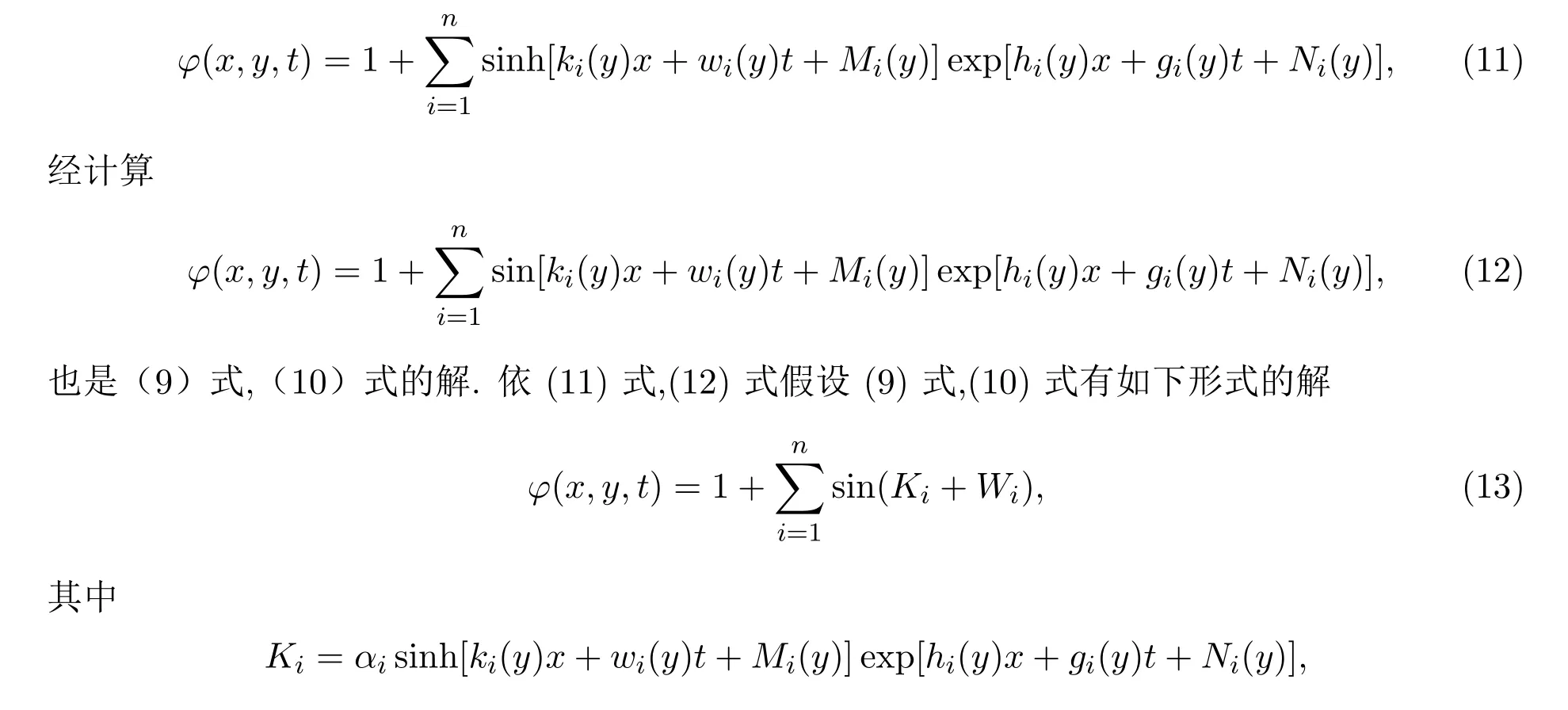
4 (2+1)維耗散長波方程新解的局域激發(fā)與分形結(jié)構(gòu)

本文中(2+1)維耗散長波方程(1)(2)的解u(x,y,t)和η(x,y,t)之間存在變換

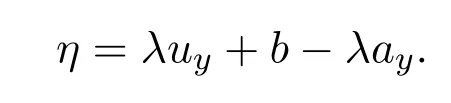
所以只討論解u(x,y,t)的情況.限于篇幅,討論了當(dāng)n=1時(shí),u(x,y,t)的局域激發(fā)與分形結(jié)構(gòu).

當(dāng)n=1時(shí),解u(x,y,t)簡化為如下形式:

其中

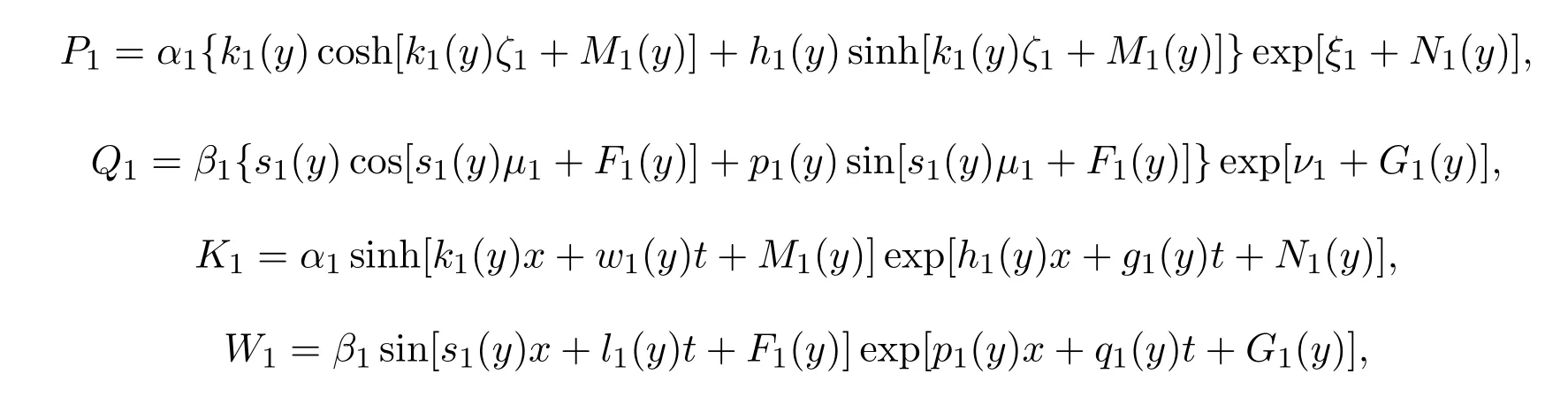
4.1 局域激發(fā)

圖1 扭結(jié)解

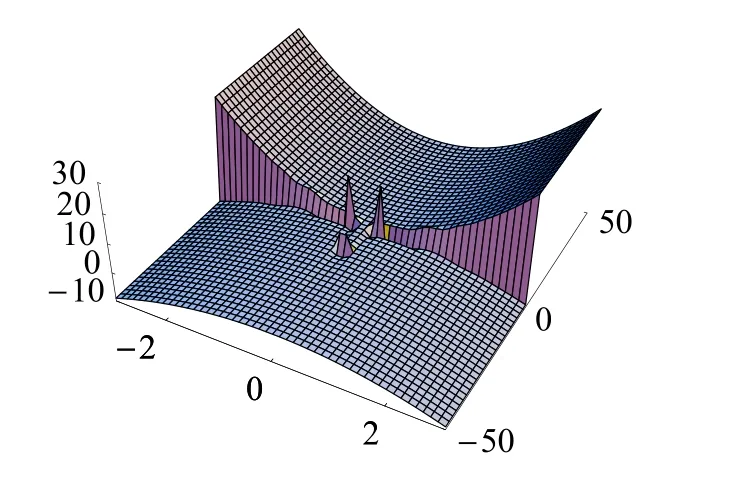
圖2 函數(shù)選取情況為4.1.2

圖3 方形孤波角

圖4 函數(shù)選取情況為4.1.4

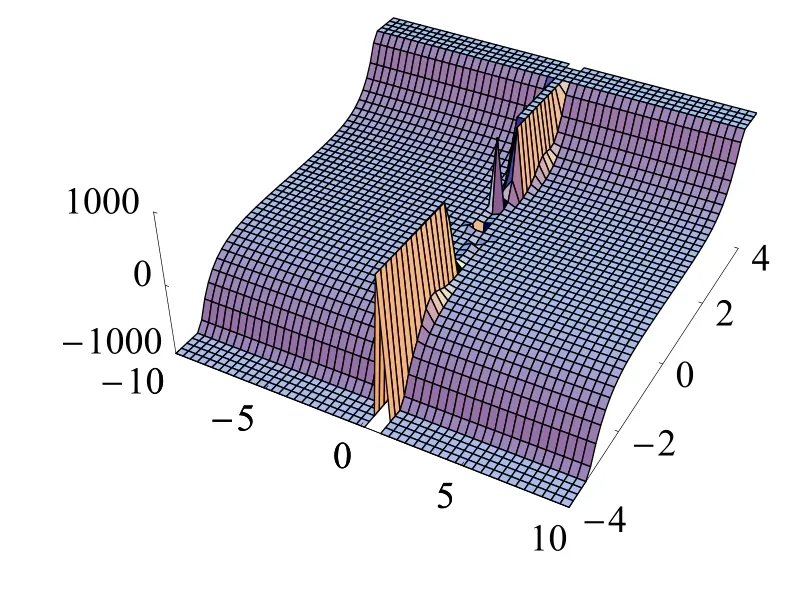
圖5 函數(shù)選取情況為4.1.5

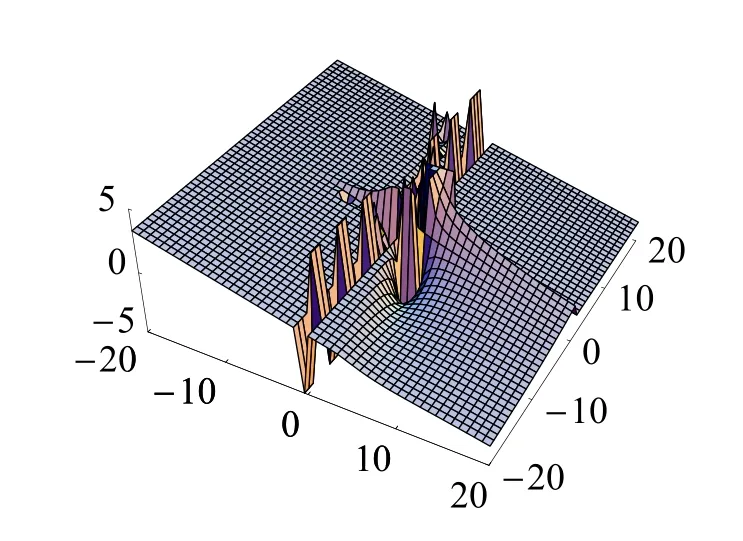
圖6 函數(shù)選取情況為4.1.6

4.2 分形結(jié)構(gòu)

圖8的每個(gè)坐標(biāo)范圍是圖7的相應(yīng)坐標(biāo)范圍的百分之一.但是,圖7和圖8的形狀具有相似性,并且當(dāng)坐標(biāo)范圍一直向下取時(shí)得到的圖形也具有完全類似的結(jié)構(gòu).

圖7 x∈[?0.002,0.002],y∈[?0.002,0.002]時(shí),解(16)的圖形

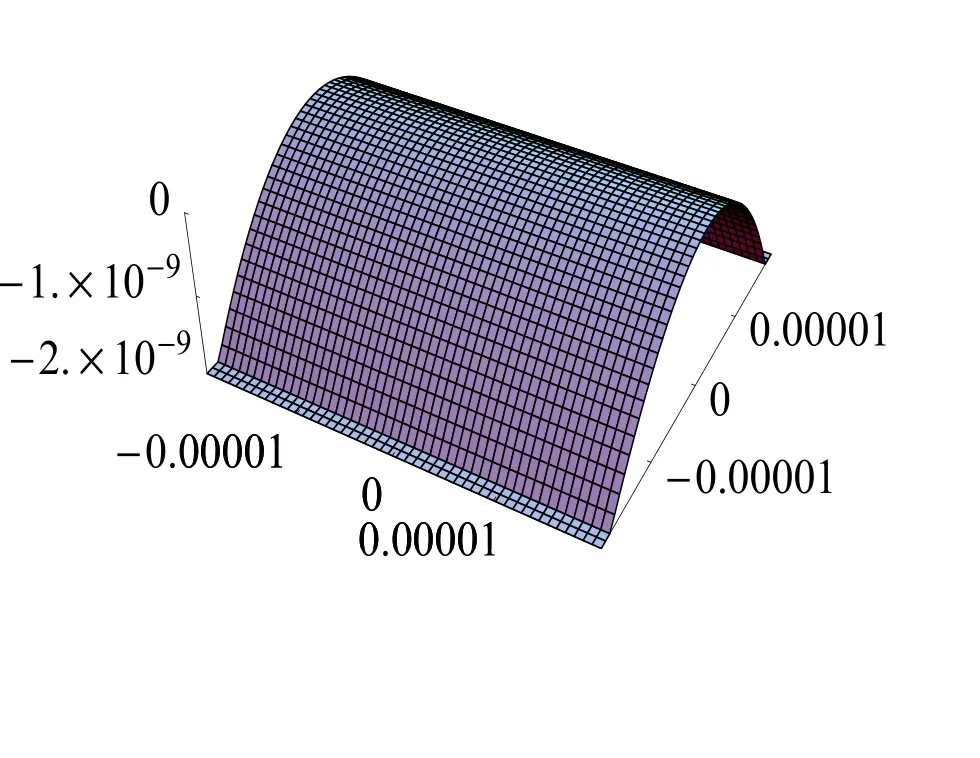
圖8 x∈[?0.00002,0.00002],y∈[?0.00002,0.00002]時(shí),解(16)的圖形

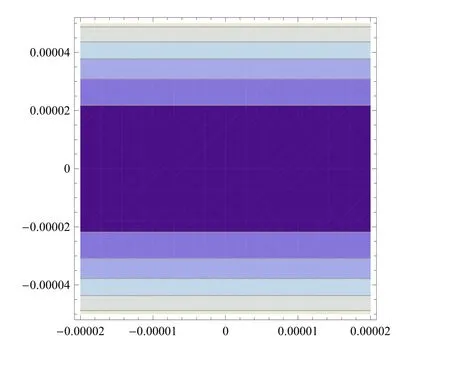
圖9 圖7的等值線圖

圖10 圖8的等值線圖

圖9和圖10分別是圖7和圖8的等值線圖.

5 結(jié)論

本文改進(jìn)了雙曲正切函數(shù)展開法,獲得了(2+1)維耗散長波方程的復(fù)合型新解.復(fù)合型新解中含有關(guān)于變量的任意函數(shù),對(duì)新解中含有變量的任意函數(shù)進(jìn)行適當(dāng)選應(yīng)用此方法也可以獲得(2+1)維Broer-kaup方程的復(fù)合型新解,復(fù)合型新解中同樣含有關(guān)于變量的任意函數(shù).

[1]李志斌,張善卿.非線性波方程準(zhǔn)確孤立波解的符號(hào)計(jì)算[J].數(shù)學(xué)物理學(xué)報(bào),1997,17(1):81-89.

[2]套格圖桑,斯仁道爾吉.雙曲函數(shù)型輔助方程構(gòu)造具 5次強(qiáng)非線性的波動(dòng)方程的新精確孤波解 [J].物理學(xué)報(bào),2006,55(1):13-18.

[3]王三五,于鵬.擴(kuò)展的Tanh函數(shù)展開法與廣義KdV方程的精確解[J].科學(xué)技術(shù)與工程,2009,9(11):3019-3020.

[4]劉德剛.求解Burgers方程行波解的雙曲函數(shù)展開法[J].黑龍江工程學(xué)院學(xué)報(bào):自然科學(xué)版,2009,23(4):77-78.

[5]張睿,張玉春,王彬弟.應(yīng)用拓展雙曲函數(shù)方法求KP方程的新精確解[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2010,26(4):651-655.

[6]那仁滿都拉,王克協(xié).(2+1)維耗散長波方程與 (2+1)維 Broer-Kaup方程新的類多孤子解 [J].物理學(xué)報(bào),2003,52(7):1565-1568.

[7]張解放.(2+1)維耗散長波方程的類多孤波解[J].浙江工業(yè)大學(xué)學(xué)報(bào),1999,27(1):77-81.

[8]包霞,斯仁道爾吉.(2+1)維耗散長波方程與(2+1)維Broer-Kaup方程新的類孤子解[J].西北民族大學(xué)學(xué)報(bào):自然科學(xué)版,2006,27(57):18-22.

[9]陳麗瑩.(2+1)維耗散長波方程的行波解[J].內(nèi)蒙古民族大學(xué)學(xué)報(bào),2012,18(5):3-4.

New exact solutions of the(2+1)-dimensional dispersive long wave equations and their local excitation

Liu Wei,Taogetusang
(The College of Mathematical Science,Inner Mongolia Normal University,Hohhot 010022,China)

Based on the improved expansion method with hyperbolic tangent function,the new type compound solutions of the(2+1)dimensional dispersive long wave equation,by combination of exponential function and trigonometric function and hyperbolic function,were obtained.There is an arbitrary function about the variable y in it.According to the arbitrariness of the functions and the numerical simulation of the solutions through the symbolic computation system Mathematica,the rich local excitation and fractal structure have been got.

modi fi ed hyperbolic function expansion method, (2+1)-dimensional dispersive long wave equations,local excitation,fractal structures

O175.29

A

1008-5513(2017)01-0102-09

10.3969/j.issn.1008-5513.2017.01.0011

2016-09-28.

國家自然科學(xué)基金(11361040);內(nèi)蒙古自治區(qū)自然科學(xué)基金(2015MS0128);內(nèi)蒙古自治區(qū)高等學(xué)?？茖W(xué)研究基金(NJZY16180);內(nèi)蒙古師范大學(xué)碩士研究生科研創(chuàng)新基金(CXJJS16081).

劉威(1991-),內(nèi)蒙古,碩士生.研究方向：孤立子與可積系統(tǒng)理論及應(yīng)用.

套格圖桑(1964-),教授,博士,從事孤立子與可積系統(tǒng)理論及應(yīng)用.

2010 MSC:35C08