?
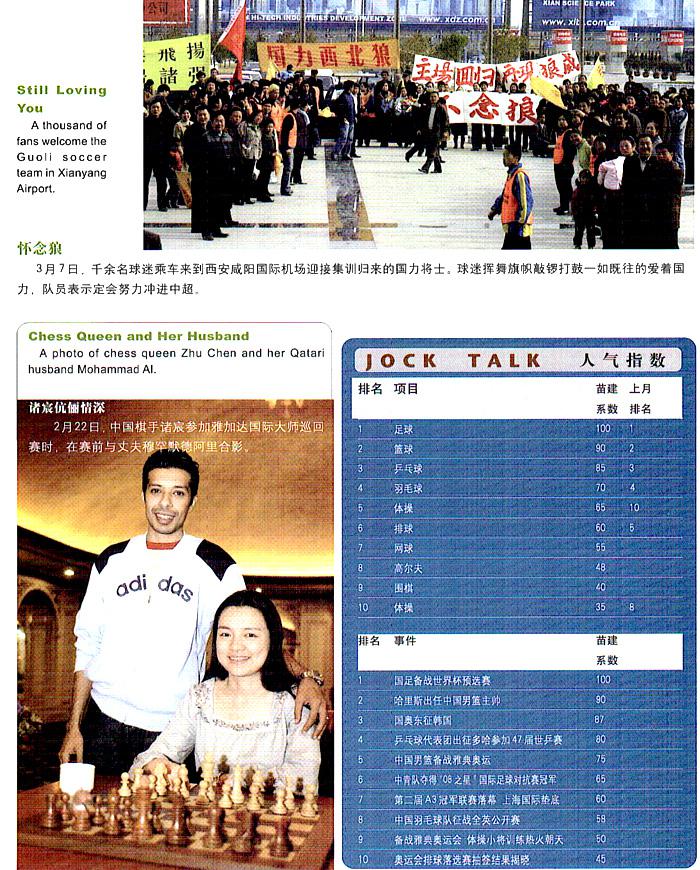
萬花筒 人氣指數(shù)
2004-11-16 08:03:18
男女排球?qū)?/p>
巾幗挑戰(zhàn)越野車賽
奧組委的人情味
女排慶三八
……





在线播放免费人成毛片乱码|
日本视频一区二区二区|
日本人妻高清免费v片|
色欲一区二区三区精品a片|
亚洲av成人中文无码专区|
国产91网址|
日本午夜一区二区视频|
东京热日本av在线观看|
米奇7777狠狠狠狠视频影院|
啪啪免费网站|
日本熟女人妻一区二区三区|
日本中文一区二区在线|
成人毛片无码一区二区三区|
色丁香久久|
91久久精品一区二区喷水喷白浆|
亚洲毛片一区二区在线|
性高湖久久久久久久久|
日韩我不卡|
色老板在线免费观看视频日麻批|
青青手机在线观看视频|
a级毛片免费观看网站|
日本久久久免费高清|
天堂麻豆精品在线观看|
国内精品久久久久影院优|
国产成人久久精品77777综合|
久久99精品波多结衣一区|
日本一区二区不卡在线|
色哟哟精品视频在线观看|
中文字幕亚洲无线码在一区|
国产精品久久国产精品久久|
中国国产不卡视频在线观看|
摸进她的内裤里疯狂揉她动视频|
亚洲人成网站久久久综合|
伊人久久亚洲精品中文字幕|
2019日韩中文字幕mv|
国产精品天堂|
日韩美女人妻一区二区三区|
亚洲国产精品日本无码网站|
蜜臀aⅴ国产精品久久久国产老师|
国产极品喷水视频|
白白色发布会在线观看免费|








