顧金劍,劉文德

(哈爾濱師范大學(xué)數(shù)學(xué)系,黑龍江哈爾濱150025)

3維冪零李超代數(shù)的Yang-Baxter算子

顧金劍,劉文德

(哈爾濱師范大學(xué)數(shù)學(xué)系,黑龍江哈爾濱150025)

在復(fù)數(shù)域C上,利用3維冪零李超代數(shù)的分類,通過計(jì)算刻畫了3維冪零李超代數(shù)的Yang-Baxter算子.

Yang-Baxter算子;冪零李超代數(shù);Yang-Baxter方程

1 引言

Baxter于1960年提出Baxter算子的概念[1].Rota在60年代初給出了很多Baxter算子的例子[2],并提出Rota-Baxter算子的概念.無論在數(shù)學(xué)還是物理領(lǐng)域,Rota-Baxter算子都被廣泛的應(yīng)用,如:Yang-Baxter方程[3]、量子場(chǎng)理論[4-5].物理學(xué)家在80年代發(fā)現(xiàn)了經(jīng)典Yang-Baxter關(guān)系與Baxter代數(shù)的關(guān)系.文獻(xiàn)[6]系統(tǒng)的研究了經(jīng)典Yang-Baxter方程,發(fā)現(xiàn)了經(jīng)典Yang-Baxter方程與左對(duì)稱代數(shù)有密切關(guān)系,證明了Yang-Baxter算子可以用線性映射表示,并且此線性映射滿足與Rota-Baxter算子相似的等式.文獻(xiàn)[7]表明Rota-Baxter關(guān)系不僅僅對(duì)結(jié)合代數(shù)成立,對(duì)李代數(shù)和pre-李代數(shù)依然成立.Rota在90年代推進(jìn)了關(guān)于Baxter算子方面的研究.從20世紀(jì)80年代起,Yang-Baxter系統(tǒng)一直是數(shù)學(xué)和物理領(lǐng)域最重要的研究課題之一.文獻(xiàn)[8]刻畫了(G,Θ)李代數(shù)的Yang-Baxter算子,文獻(xiàn)[9]證明了Yang-Baxter算子與Hom-李代數(shù)有密切關(guān)系,但很少有關(guān)于李超代數(shù)Yang-Baxter算子具體形式的研究.

李超代數(shù)是非常重要的研究領(lǐng)域,而冪零李超代數(shù)在李超代數(shù)中占有重要地位.事實(shí)上,計(jì)算出冪零李超代數(shù)的Yang-Baxter算子是一項(xiàng)十分有意義的工作.雖然一般冪零李超代數(shù)的分類還沒有實(shí)現(xiàn),但是利用低維冪零李超代數(shù)的分類定理可以計(jì)算出某些低維冪零李超代數(shù)的所有Yang-Baxter算子,從而為計(jì)算高維冪零李超代數(shù)的Yang-Baxter算子提供參考.

本文利用3維冪零李超代數(shù)在同構(gòu)意義下的分類[10],刻畫了復(fù)數(shù)域上3維冪零李超代數(shù)的所有Yang-Baxter算子.

2 基本概念和引理

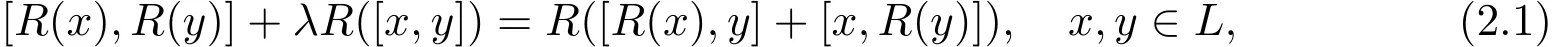
Abel李超代數(shù)是特殊的冪零李代數(shù),由于Abel李超代數(shù)的任意線性變換均為Yang-Baxter算子,所以本文只考慮非Abel冪零李超代數(shù)的Yang-Baxter算子.

下面列出非Abel冪零李超代數(shù)在同構(gòu)意義下的分類:

引理2.1[10]C上的任意3維非Abel冪零李超代數(shù)必同構(gòu)于如下3類李超代數(shù)之一:

(1)L3,1,它具有一個(gè)基{a|α,β},基元素之間的非零李乘如下:[a,β]=α;

(2)L3,2,它具有一個(gè)基{a|α,β},基元素之間的非零李乘如下:[α,α]=a,[β,β]=a;

(3)L3,3,它具有一個(gè)基{a|α,β},基元素之間的非零李乘如下:[α,α]=a,[β,β]=?a.

令{x1,...,xn}是L的一組固定基,并設(shè)

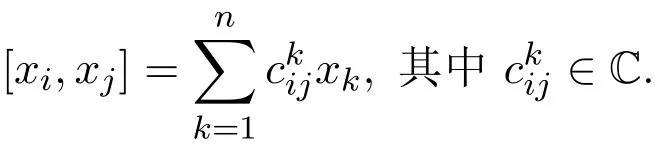
以下將L上的Yang-Baxter算子R寫成矩陣(rij)形式,其中(rij)由等式唯一確定.

注記2.1當(dāng)i=0時(shí),Rij簡(jiǎn)記為Rj.

3 冪零李超代數(shù)的Yang-Baxter算子

引理3.1冪零李超代數(shù)L3,1的權(quán)為0的Yang-Baxter算子有6種,分別是Rij,其中i=0,j=1,………,6;冪零李超代數(shù)L3,1的權(quán)為1的Yang-Baxter算子有8種,分別是Rij,其中,當(dāng)i=0時(shí),j=7,………,9;當(dāng)i=1時(shí),j=0,………,4(Rij的具體形式見證明).

證明利用L3,1的乘法表分四種情況計(jì)算:

(1)當(dāng)λ=0且R是奇線性映射時(shí),有

于是,R滿足(2.1)式,當(dāng)且僅當(dāng),r21=0,r13r31=0,所以L3,1的權(quán)為0的奇Yang-Baxter算子為:

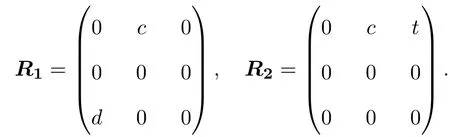
(2)當(dāng)λ=0且R是偶線性映射時(shí),有

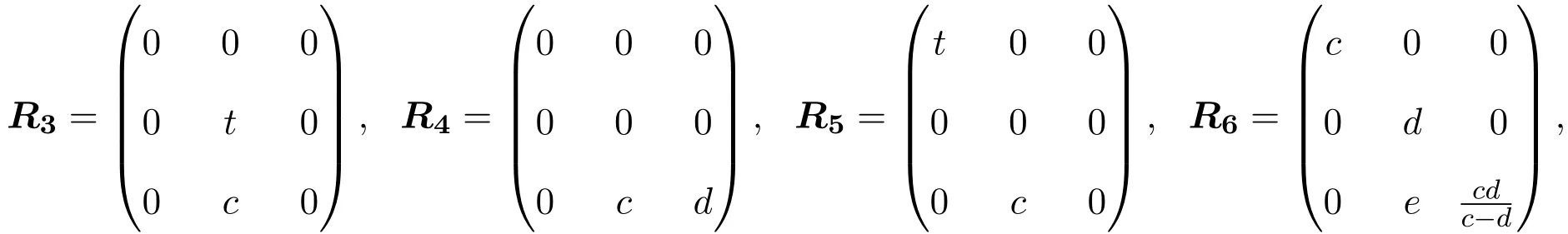
其中c/=d.

(3)當(dāng)λ=1且R是奇線性映射時(shí),有(3.1)-(3.3)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)r21=0,r13r31=0.此時(shí)的Yang-Baxter算子具有的矩陣形式與L3,1的權(quán)為0的奇Yang-Baxter算子相同,所以L3,1的權(quán)為1的Yang-Baxter算子為:R7=R1,R8=R2.

(4)當(dāng)λ=1且R是偶線性映射時(shí),有(3.4)-(3.6)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)r23=0,r11r33+r22?r22(r33+r11)=0,所以L3,1的權(quán)為1的偶Yang-Baxter算子為:

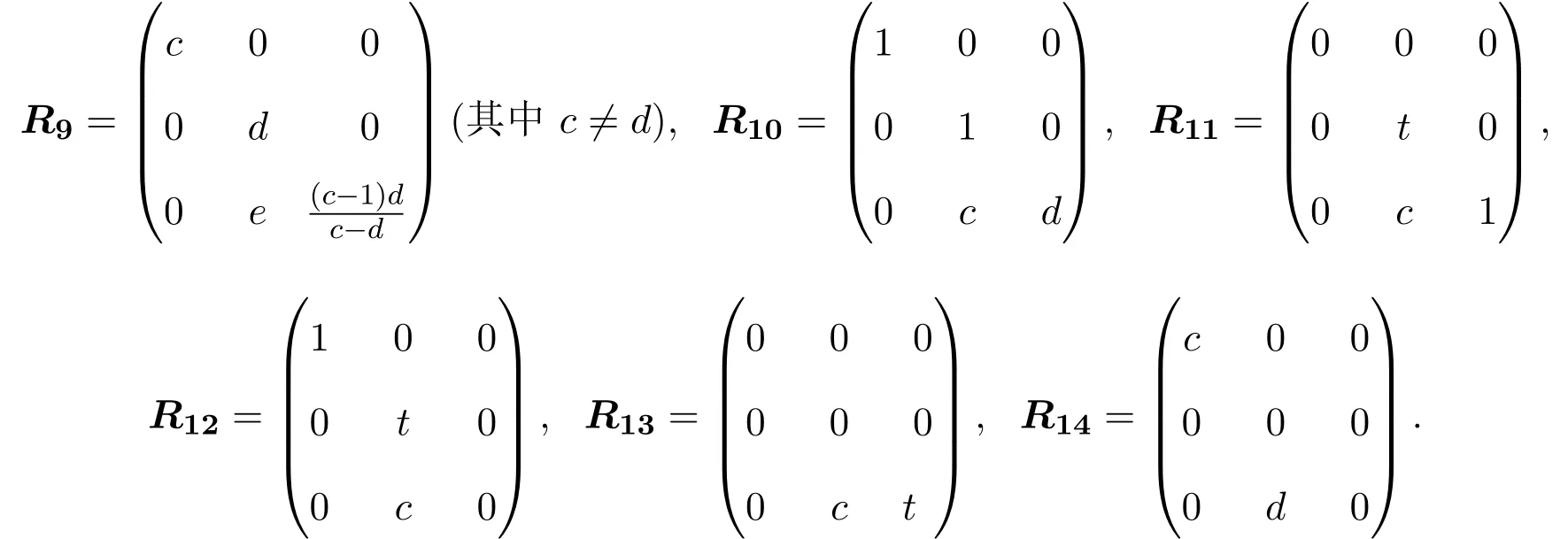
引理3.2冪零李超代數(shù)L3,2的權(quán)為0的Yang-Baxter算子有6種,分別是Rij,其中,當(dāng)i=1時(shí),j=5,………,9;當(dāng)i=2時(shí),j=0;冪零李超代數(shù)L3,2的權(quán)為1的Yang-Baxter算子有13種,分別是Rij,其中,當(dāng)i=2時(shí),j=1,………,9;當(dāng)i=3時(shí),j=0,………,3(Rij的具體形式見證明).

證明利用L3,2的乘法表分四種情況計(jì)算:

(1)當(dāng)λ=0且R是奇線性映射時(shí),有(3.1)-(3.3)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)r12=r13=0,所以L3,2的權(quán)為0的奇Yang-Baxter算子為:

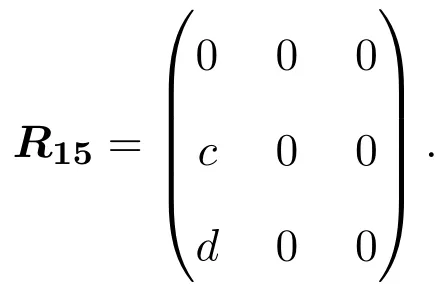
(2)當(dāng)λ=0且R是偶線性映射時(shí),有(3.4)-(3.6)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)

所以L3,2的權(quán)為0的偶Yang-Baxter算子為:

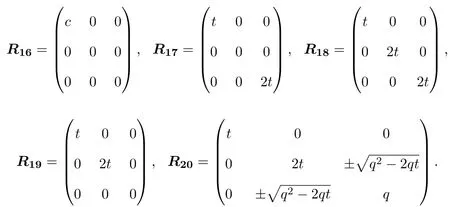
(3)當(dāng)λ=1且R是奇線性映射時(shí),有(3.1)-(3.3)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)r12=r13=0.此時(shí)Yang-Baxter算子具有的矩陣形式與L3,2的權(quán)為0的奇Yang-Baxter算子相同,所以L3,2的權(quán)為1的奇Yang-Baxter算子為:R21=R15.

(4)當(dāng)λ=1且R是偶線性映射時(shí),有(3.4)-(3.6)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)

此時(shí)Yang-Baxter算子具有的矩陣形式與L3,2的權(quán)為0的偶Yang-Baxter算子相同,所以L3,2的權(quán)為1的偶Yang-Baxter算子為:

引理3.3冪零李超代數(shù)L3,3的權(quán)為0的Yang-Baxter算子有9種,分別是Rij,其中,當(dāng)i=3時(shí),j=4,………,9;當(dāng)i=4時(shí),j=0,………,2;冪零李超代數(shù)L3,3的權(quán)為1的Yang-Baxter算子有18種,分別是Rij,其中,當(dāng)i=4時(shí),j=3,………,9;當(dāng)i=5時(shí),j=0,………,9;當(dāng)i=6時(shí),j=0(Rij的具體形式見證明).

證明利用L3,3的乘法表分四種情況計(jì)算:

(1)當(dāng)λ=0且R是奇線性映射時(shí),有(3.1)-(3.3)式均成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)r12=r13=0.所以L3,3的權(quán)為0的奇Yang-Baxter算子為:R34=R15.

(2)當(dāng)λ=0且R是偶線性映射時(shí),有(3.4)-(3.6)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)

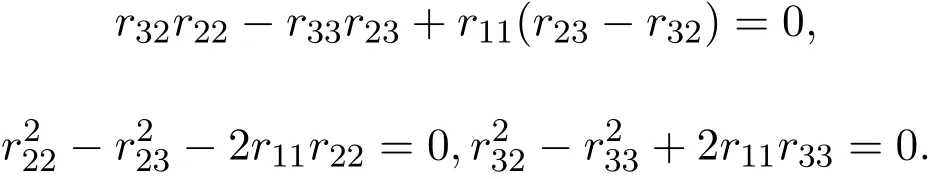
所以L3,3的權(quán)為0的偶Yang-Baxter算子為:

(3)當(dāng)λ=1且R是奇線性映射時(shí),有(3.1)-(3.3)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)r12=r13=0.此時(shí)Yang-Baxter算子具有的矩陣形式與L3,3的權(quán)為0的奇Yang-Baxter算子相同,所以L3,3的權(quán)為1的奇Yang-Baxter算子為:R43=R15.

(4)當(dāng)λ=1且R是偶線性映射時(shí),有(3.4)-(3.6)式成立,于是,R滿足(2.1)式,當(dāng)且僅當(dāng)

此時(shí)Yang-Baxter算子具有的矩陣形式與L3,3的權(quán)為0的偶Yang-Baxter算子相同,所以L3,3的權(quán)為1的偶Yang-Baxter算子為:

由引理3.1至引理3.3可以得出如下定理:

定理3.43維非Abel冪零李超代數(shù)L的Yang-Baxter算子Rij如表1所列:

表13維非Abel冪零李超代數(shù)L的Yang-Baxter算子Rij

其中,Rij的具體形式見引理3.1至引理3.3的證明.

[1]Baxter G.An analytic problem whose solution follows from a simple algebraic identity[J].Paci fi c J.Math., 1960,10(3):731-742.

[2]Rota G C,Smith D A.Fluctuation Theory and Baxter Algebras[C].Symposia Math.,1972,9:179-201.

[3]Aguiar M.On the associative analog of Lie bialgebras[J].J.Algebra,2001,244(2):492-532.

[4]Ebrahimi-Fard K,Guo L,Kreimer D.Spitzer′s identity and the algebraic Birkho ffdecompositon in pQFT[J]. J.Phys.A:Math.Gen.,2004,37(45):11037-11052.

[5]Connes A,Kreimer D.Hopf Algebras,Renormalization and Noncommutative Geometry[M].Netherlands: Springer,1999.

[6]Bai C.A uni fi ed algebraic approach to the classical Yang-Baxter equation[J].J.Phys.A:Math.Theory, 2007,40(36):11073-11082.

[7]Ebrahimi-Fard K,Guo L,Kreimer D.Integrable renormalization I:the ladder case[J].J.Math.Phys., 2004,45:3758-3769.

[8]Nichita F F.Lie algebras and Yang-Baxter equations[J].arXiv:1107.0920v1.

[9]Yau Donald.The Hom-Yang-Baxter equation and Hom-Lie algebras[J].J.Math.Phys.,2011,52(5):3502-3520.

[10]Backhouse Nigel.A classi fi cation of four dimensional Lie superalgebras[J].J.Math.Phys.,1978,19(11):2400-2402.

Yang-Baxter operators on the Lie superalgebras of dimension three

Gu Jinjian,Liu Wende
(School of Mathematical Sciences,Harbin Normal University,Harbin150025,China)

Let C be a complex fi eld.In this paper,employing the classi fi cation of Lie superalgebras of dimension 3,we fi nd out all the Yang-Baxter operators on the nilpotent Lie superalgebras of dimensions 3.

Yang-Baxter operators,Nilpotent Lie superalgebras,Yang-Baxter equation

O152.5

A

1008-5513(2014)03-0307-07

10.3969/j.issn.1008-5513.2014.03.013

2014-01-18.

黑龍江省教育廳科學(xué)研究基金(12511349);國(guó)家自然科學(xué)基金(11171055);黑龍江省杰出青年基金(JC201004).

顧金劍(1989-),碩士生,研究方向：李代數(shù)與李超代數(shù).

劉文德(1965-),博士,教授,博士生導(dǎo)師,研究方向：李代數(shù)與李超代數(shù).

2010 MSC:17B20,17B40,17B50