賈慶菊

(山西財經(jīng)大學應(yīng)用數(shù)學學院,山西太原030006)

一類高階變系數(shù)線性非齊次微分方程的解

賈慶菊

(山西財經(jīng)大學應(yīng)用數(shù)學學院,山西太原030006)

利用高階變系數(shù)之間的關(guān)系,通過適當?shù)木€性變換,得到了五階變系數(shù)線性非齊次方程常系數(shù)化的條件,給出了一類高階變系數(shù)線性非齊次微分方程的新解法.

高階;變系數(shù)線性非齊次微分方程;線性變換;常系數(shù)線性非齊次微分方程

1 引言

線性微分方程在科學研究、工程技術(shù)中有著廣泛的應(yīng)用.常系數(shù)線性微分方程,利用特征方程和常數(shù)變易法,求解問題已經(jīng)徹底解決.但在生產(chǎn)實踐以及經(jīng)濟領(lǐng)域中,人們常會遇到二階或更高階變系數(shù)線性微分方程.因此,探討它們的解法具有重要理論意義和使用價值.這類方程雖然在理論上證明了解的存在性,但在實際求解中并不如意,尤其是高階變系數(shù)線性非齊次微分方程沒有一般的解法.為了滿足理論研究和工程實踐的需要,人們用不同的方法不斷擴大變系數(shù)線性微分方程的可積類型,取得了不少成果.文獻[1-3]討論二階變系數(shù)線性方程求解;文獻[4-5]利用首次積分或變量代換將高階微分方程化為可求解的微分方程,求解的基本原則是降階的;文獻[6-8]僅討論了二階變系數(shù)線性齊次方程常系數(shù)化問題.受著名的歐拉(Euler)方程的啟發(fā),試圖尋找一種新的求解高階變系數(shù)線性非齊次方程方法.那么,高階變系數(shù)線性非齊次方程能否常系數(shù)化?常系數(shù)化的條件又是什么?本文借助高階變系數(shù)之間的關(guān)系,通過適當?shù)淖兞刻鎿Q,將一類高階變系數(shù)線性非齊次微分方程化為高階常系數(shù)線性非齊次微分方程求解.

2 主要結(jié)果及證明

定理1五階變系數(shù)線性非齊次微分方程:

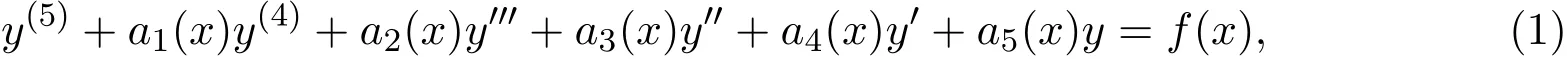
當系數(shù)滿足:

其中,mi(i=1,2,3,4)為常數(shù).可通過變換

將(1)式化為五階常系數(shù)線性非齊次微分方程求解.

證明令則

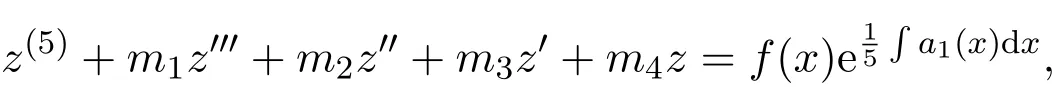
求出通解回代原來變量可得原方程通解.

定理2四階變系數(shù)線性非齊次微分方程:

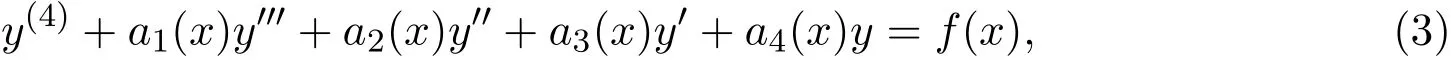
當系數(shù)滿足:

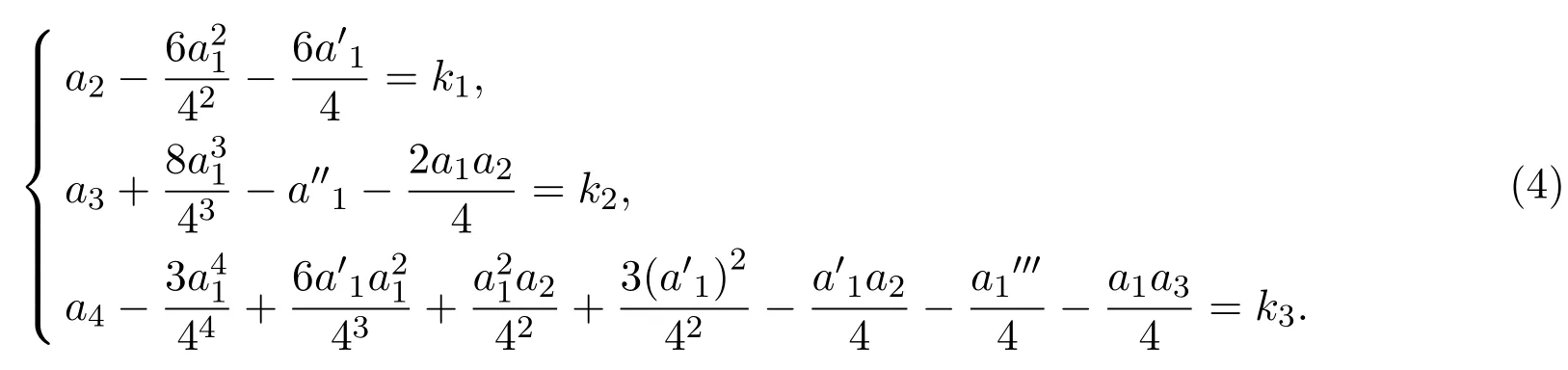
其中,ki(i=1,2,3)為常數(shù).可通過變換

將(3)式化為四階常系數(shù)線性非齊次微分求解.

證明令則

將y,y′,y′,y′′,y(4)及(4)式代入(3)式得到易求解四階常系數(shù)線性非齊次微分方程:

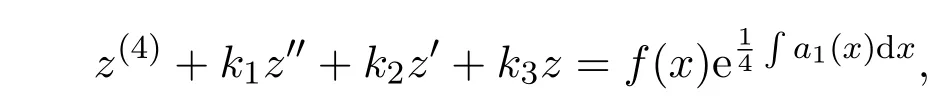
求出通解回代原來變量可得原方程通解.

定理3三階變系數(shù)線性非齊次微分方程:

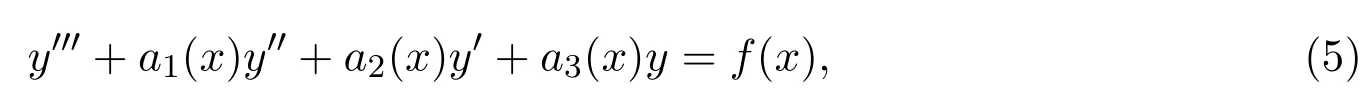
當系數(shù)滿足:

其中,bi(i=1,2)為常數(shù).可通過變換

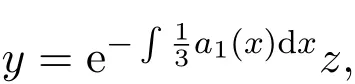
將(5)式化為三階常系數(shù)線性非齊次微分方程求解.

證明令

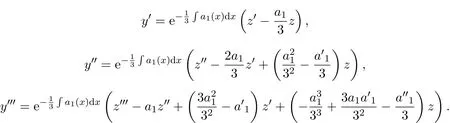
將y,y′,y′,y′′及(6)式代入(5)式可得易求解的三階常系數(shù)線性非齊次微分方程:

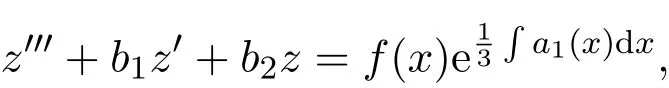
求出通解回代原來變量可得原方程通解.

定理4[3]二階變系數(shù)線性非齊次微分方程

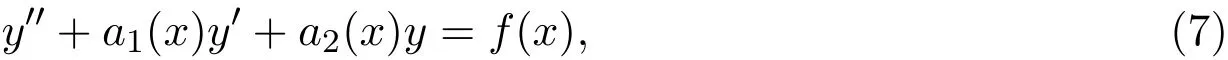
當系數(shù)滿足:

3 主要結(jié)論的應(yīng)用

例1[7]求解方程xy′+2y′?xy=ex.

解x/=0原方程改寫為:

因為

所以,(9)式可通過變換:

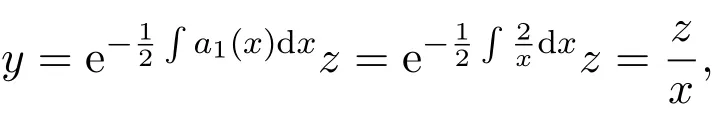
化為二階常系數(shù)線性非齊次微分方程:

例2[8]求解方程x2y(4)+8xy′′+12y′+x2y=2ex.

解x/=0原方程改寫為:

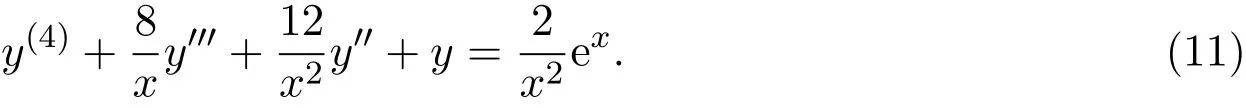
因為

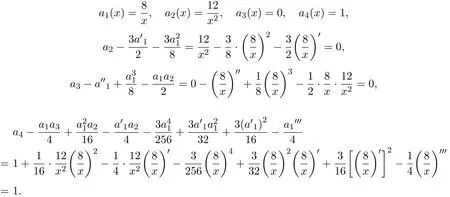
所以,(11)式可通過變換

化為四階常系數(shù)線性非齊次微分方程:

用比較系數(shù)法求得(12)式通解:

代回原來變量y,得到原方程的通解:

4 結(jié)束語

類似地,可以給出六階變系數(shù)線性非齊次微分方程常系數(shù)化的條件.順便指出,用這種方法可以得到更高階變系數(shù)線性非齊次微分方程常系數(shù)化的條件,只是計算比較復(fù)雜.

[1]彭仕章.一類可積二階變系數(shù)線性非齊次常微分方程[J].純粹數(shù)學與應(yīng)用數(shù)學,1993,9(2):99-100.

[2]馮偉杰,魏光美.二階變系數(shù)線性微分方程的通解[J].高等數(shù)學研究,2012,15(3):28-30.

[3]敏志奇.一類變系數(shù)線性微分方程的可積定理及應(yīng)用[J].甘肅高師學報,2010,15(2):6-7.

[4]賈慶菊.高階變系數(shù)線性微分方程的解[J].中央民族大學學報學報:自然科學版,2012,21(2):32-35.

[5]賈慶菊,馮文俊,武躍祥.某些黎卡蒂(Riccati)方程的解[J].中央民族大學學報學報:自然科學版,2013, 22(1):48-51.

[6]王高雄,周之銘,朱思銘.常微分方程[M].3版.北京:高等教育出版社,2006.

[7]鐘益林,彭樂群,劉炳文.常微分方程及其Maple,Matlab求解[M].北京:清華大學出版社,2007.

[8]莊萬.常微分方程習題解[M].2版.山東:山東科學技術(shù)出版社,2004.

A solution of higher-order variable coefficient nonhomogeneous linear di ff erential equation

Jia Qingju
(Faculty of Applied Mathematics of Shanxi University Finance and Economics,Taiyuan030006,China)

The paper,by using higher-order relationship between of variable coefficient,through appropriate linear transformations of variables,and won fi ve-order variable coefficients linear di ff erential equation with constant sufficient conditions,gives a new solution to the higher-order variable coefficients linear non-homogeneous di ff erential equations.

higher-order,variable coefficients linear non-homogeneous di ff erential equation, linear transformation,constants coefficients linear non-homogeneous di ff erential equation, sufficient condition

O175

A

1008-5513(2014)03-0234-06

10.3969/j.issn.1008-5513.2014.03.003

2014-04-15.

國家自然科學基金(11126027);山西財經(jīng)大學校級教改項目(2013132);山西財經(jīng)大學校級教學團體項目.

賈慶菊(1956-),副教授,研究方向:常微分方程與應(yīng)用數(shù)學.

2010 MSC:34B15