張齊,朱輝輝

(1.銅陵學院數(shù)學與計算機學院,安徽銅陵244000;2.東南大學數(shù)學系,江蘇南京210096)

相對n-FP-內射模

張齊1,朱輝輝2

(1.銅陵學院數(shù)學與計算機學院,安徽銅陵244000;2.東南大學數(shù)學系,江蘇南京210096)

給出了n-FP-內射模的定義,M為左R-模,如果對任意的左R-模N有Ext1(N,M)=0,則稱M為n-FP-內射模,作為應用,給出了n-FP-內射模的一些等價條件.

余撓理論;FP-投射維數(shù);n-FP-內射模;(預)覆蓋

1 引言

本文中,R表示有單位元的結合環(huán),所有的模均指酉模,記M表示左R模.令0→M→E0→E1→………為模M的一個內射分解,其中L0=M,L1=Im(E0→E1), Li=Im(Ei?1→Ei),稱Ln為M的第n個上合沖[1].符號wD(R),pd(M)和id(M)分別表示環(huán)R的弱整體維數(shù),模M的投射維數(shù)以及內射維數(shù).用HomR(M,N)((M,N))表示Hom(M,N)(Extn(M,N)).如果對任意的有限表示R-模N都有Ext1(M,N)=0,稱M為FP-投射模.模M的FP-投射維數(shù)(FP-fd(M))定義為最小的數(shù)n≥0使得Extn+1(M,N)=0(N為有限表示的左R-模),如果這樣的n不存在,定義FP-fd(M)=∞, l.FP?dim(R)定義為sup{FP-fd(M),M為左R-模},FPn(FCn)表示所有FP-投射維數(shù)(FP-內射維數(shù))小于等于n的左R-模類.

環(huán)R被稱為左凝聚環(huán)如果R的每個有限生成左理想都是有限表示的,左R-模類(F,C)稱為余撓的,如果F⊥=C和⊥C=F,其中

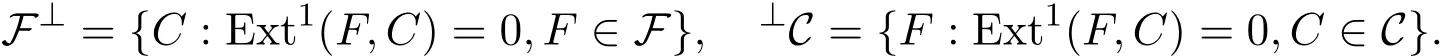
設C為左R-模類,同態(tài)?:M→F稱為模F的C-預覆蓋(M∈C),如果對任意的f:M′→F,存在同態(tài)g:M′→M使得f=?g.如果同態(tài)g是M的同構,則F的C-預覆蓋叫做F的C-覆蓋.對偶地,可以定義C-預包絡和C-包絡.由文獻[2]知,如果Kerβ∈C⊥,則同態(tài)β:F→M(F∈C)為M的一個特殊C-預覆蓋.顯然,特殊的C-預覆蓋是C預覆蓋.

1993年,文獻[3]討論了內射模的投射維數(shù).2005年,文獻[2]考慮了相對FP-投射模,并且給出了相對FP-投射模的一些等價條件.更多關與投射模,內射模的結果可參考文獻[4-10].受文獻[2]啟發(fā),考慮相對n-FP-內射模及其相關性質.因此,一些關于相對FP-內射模的結果是本文的推論.

2 定義及主要結果

首先,給出n-FP-內射模的定義.

定義2.1設R為任意環(huán),n為非負數(shù),M為左R-模,如果對任意的左R-模N(FP-fd(N)≤n)都有Ext1(N,M)=0.則稱M為n-FP-內射模.把0-FP-內射模稱為FP-內射模.

對左R-模M,設vR(M)=sup{n:M為n-FP-內射模},定義vR(M)=?1如果對某些FP-投射左R-模N有Ext1(N,M)/=0.環(huán)的左維數(shù)(l.v-dim(R))定義為最小的非負數(shù)n使得vR(M)≥n,對任意的左R-模M有vR(M)=∞,如果不存在這樣的n,規(guī)定l.v-dim(R)=∞.

命題2.1

(1)m-FP-內射模一定為n-FP-內射模(m≤n);

(2)vR(M)≥n當且僅當對某個數(shù)n≥0,M為n-FP-內射模;vR(M)=∞當且僅當對任意的數(shù)m≥0,M為m-FP-內射模,當且僅當對所有的左R-模N(FP-fd(N)<∞)都有Ext1(N,M)=0;

(3)如果l.FP-dim(R)≤n,則所有的n-FP-內射左R-模類和所有的內射左R-模類是一致的,因此l.v-dim(R)≤l.FP-dim(R);

(4)若R是左凝聚環(huán)且FP-fd(M)=m,則對所有的有限表示左R-模F及k≥1,都有Extm+k(M,F)=0.

引理2.1設R為左凝聚環(huán),M為n-FP-內射左R-模(n≥0),則對任意的左R-模N (FP-fd(N)≤n+1),都有Extj(N,M)=0(j≥2).

證明對FP-fd(N)≤n+1的左R-模N,存在正合列0→K→P→N→0,其中P為投射模,FP-fd(K)≤n,由長正合列定理得:

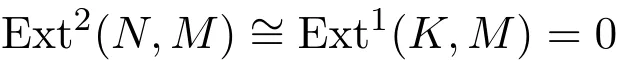
因此,Extj(N,M)=0(j≥2).

通過引理2.1知：若R是左凝聚環(huán),M為n-FP-內射左R-模,則對FP-fd(N)≤n的左R-模N及數(shù)j≥1,有Extj(N,M)=0.

命題2.2設0→A→B→C→0為左R-模正合列.有如下結論:

(1)若VR(A)≥0,則VR(C)≥inf{VR(A)+1,VR(B)};

(2)VR(B)≥inf{VR(A),VR(C)};

(3)如果B=A⊕C,則VR(A⊕C)=inf{VR(A),VR(C)}.

證明對任意的左R-模N,應用長正合列定理,可得:

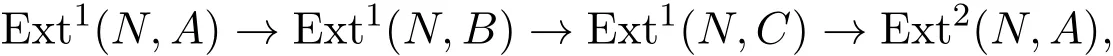
結合引理2.1即得.

推論2.1設R為有單位的結合換環(huán),則

(1)每個有限表示的左R-模的第n個上合沖Ln是n-FP-內射模;

(2)任意的有限生成的1-FP-內射模的有限生成商模是1-FP-內射模;

(3)對任意的左R-模同態(tài)α:M→N,其中M,N是有限生成的1-FP-內射模,有Im(α)是1-FP-內射模,而且如果N是2-FP-內射模,則Im(α)也是2-FP-內射模.

證明(1)設M為有限表示的左R-模,存在整合列:

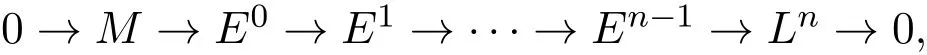
Ei(1≤i≤n?1)均為內射的,設L1=Im(E0→E1),Ei=Im(Ei?1→Ei),則0→M→E0→L1→0是正合的,既然VR(M)≥0,VR(E0)=∞(E0為內射模),由命題2.2知: VR(L1)≥inf{VR(M)+1}≥1,類推即得(1).

(2)設N為1-FP-內射左R-模M的有限生成子模,則存在如下正合列：0→N→M→M/N→0,應用命題2.2(1)即得.

(3)由Im(α)≤N得Im(α)是有限生成的,所以M/Ker(α)Im(α)是1-FP-內射的,考慮正合列:

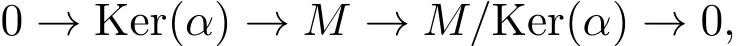
應用命題2.2(1)即得(3).

若R是Gorenstein環(huán),則每個Gorenstein內射模都是m-FP-內射模(0≤m<∞).通過文獻[2],如果R是n-Gorenstein環(huán),則左R-模M是m-FP-內射模(n≤m<∞)當且僅當M是Gorenstein內射模.

引理2.2[2]設R為左凝聚環(huán),n≥0,則()是余撓理論,而且每個左R-模都有一個特殊預包絡,每個左R-模都有一個特殊預覆蓋.

命題2.3設R為左凝聚環(huán)且對某個整數(shù)n≥0有FP-fd(RR)≤n,則下列陳述等價：

(1)M是n-FP-內射模;

(6)存在內射分解E=0→M→E0→E1→………,使得對所有的左R-模N(FP-fd(N)≤n),Hom(N,)是正合的.

證明(1)?(2)由長正和列定理得:

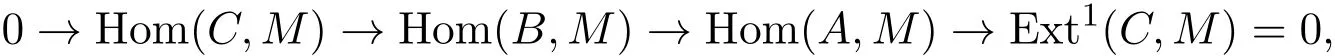
即得.

(1)?(3)顯然.

(3)?(4)設0→M→E→F→0為正合列,其中E為內射的,由FP-fd(RR)≤n,所以FP-fd(E)≤n,因此E→F是預覆蓋.

(4)?(1)由(4),存在正合列：0→M→E→F→0,其中E→F是一個預覆蓋(E為內射的).對每個N∈,存在正合列:Hom(N,E)→Hom(N,F)→Ext1(N,M)→0,由(4)Hom(N,E)→Hom(N,F)→0是正合的,因此Ext1(N,M)=0,即M是n-FP-內射模.

(1)?(5)設0→M→E0→E1→………為M的一個內射分解,由假設FP-fd(Ei)≤n (i=0,1,2,………),設N是任意的左R-模(FP-fd(N)≤n),既然M是n-FP-內射模,由引理2.3,對任意的j≥1,Extj(N,M)=0,因此序列

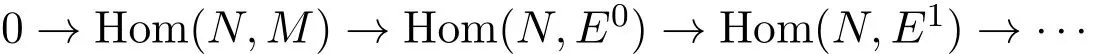
是正合的.另一方面,構造正合列………→E1→E0→M→0.由引理2.2知：E0→M, Im(E2→E1)→E0,Im(En+1→En)→En?1是-預覆蓋,因此有正合列:

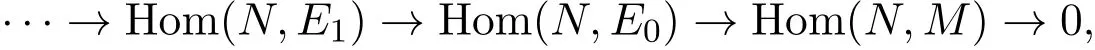
(5)?(6)顯然可得.

(6)?(1)存在M的一個內射分解0→M→E0→E1→………,對所有的左R-模N(FP-fd(N)≤n),Hom(N,E0)→Hom(N,E1)→Hom(N,E2)是正合的,結合長正合列定理即得.

定理2.1設R為左凝聚環(huán),n為非負數(shù),則下列等價:

(1)l.FP-dim(R)≤n;

(2)wD(R)≤n;

(3)每個n-FP-內射模都是內射的;

(4)對每個0-FP-內射左R-模有id(M)≤n;

(5)對每個n-FP-內射左R-模有FP-fd(M)≤n;

(7)每個(n?1)-FP-內射模M有id(M)≤1.

證明由文獻[8]可得(1)?(2)?(4).(1)?(3)和(1)?(6)是平凡的.

(3)?(1)對每個左R-模,l.FP-dim(R)≤n等價于FP-fd(M)≤n,用引理2.2可得.

(5)?(1)設M為左R-模,由引理2.2,M有個特殊的預包絡,因此存在短正合列:0→M→N→K→0,N是n-FP-內射的,由(5)知FP-fd(N)≤n,FP-fd(M)≤n,可得(1).

(1)?(4)設M為0-FP-內射左R-模,則M有一個內射分解:

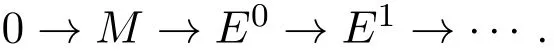
設N為任意的左R-模,FP-fd(N)≤n,(對偶與文獻[8])存在正合列:

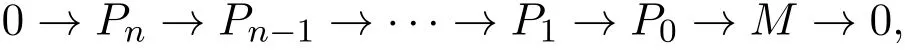
其中P0,P1,………,Pn是FP-投射的,因此可構造下面的雙復形:

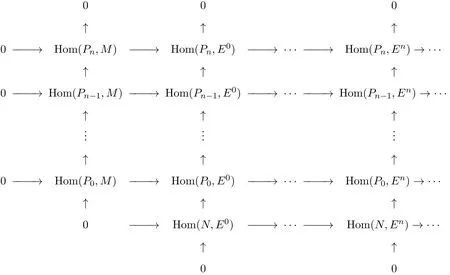
除了最下面一行外,所有的行均為正合的(M是0-FP-內射的,Pi是FP-投射的).除了左邊一列外,所有的列均正合的(Ei均為內射的).因此下面兩復形

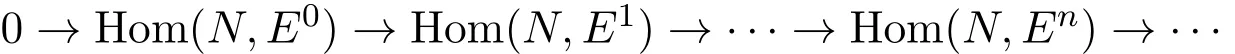
和

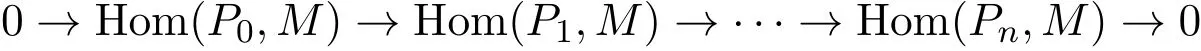
是同構同調群,而且對j≥1有Extn+j(N,M)=0,所以id(M)≤n.

(1)?(7)設M是(n?1)-FP-內射左R-模,N為任意左R-模,既然FP-fd(N)≤n,由命題2.3知Ext2(N,M)=0,所以id(M)≤1.

眾所周知,左凝聚環(huán)R是半遺傳的當且僅當wD(R)≤1,有如下結果.

推論2.2設R是左凝聚環(huán),下列條件等價:

(1)R是左半遺傳環(huán);

(2)每個1-FP-內射左R-模是內射模;

(3)每個0-FP-內射R-模的內射維數(shù)小于等于1;

(4)每個1-FP-內射R-模的FP-投射維數(shù)小于等于1.

致謝作者真誠地感謝評審專家仔細的閱讀和詳細的修改.

[1]Anderson F W,Fuller K R.Rings and Categories of Modules[M].New York:Springer,1992.

[2]Mao L X,Ding N Q.Relative FP-projective mosules[J].Communications in Algebra,2005,33:1587-1602.

[3]Ding N Q,Chen J L.The fl at dimensions of injective modules[J].Manuscripta Math.,1993,78:165-177.

[4]Enochs E E,Jenda O M G.Relative Homological Algebra[M].Berlin-New York:Walter de Gruyter,2000.

[5]Rotman J J.An Introduction to Homological Algebra[M].New York:Academic Press,1979.

[6]Trlifaj J.Covers,envelopes,and cotorsion theories[A]//Lecture notes for the workshop,“Homological Methods in Module Theory”.Cortona,2000,9:10-16.

[7]Huang Z Y,Tang G H.Self-orthogonal modules over coherent rings[J].Journal of Pure and Applied Algebra, 2001,161:167-176.

[8]Stenstrom B.Coherent rings and FP-injective modules[J].Journal of the London Mathematical Society, 1970,2(2):323-329.

[9]Garcia Rozas J R.Covers and Envelopes in the Categories of Complexes of Modules[M].New York: Springer-Verlag,1999.

[10]Xu J.Flat Covers of Modules[M].New York:Springer-Verlag,1996.

Relative n-FP-injective modules

Zhang Qi1,Zhu Huihui2
(1.School of mathematics and computer science,Tongling University,Tongling244000,China; 2.Department of Mathematics,Southeast University,Nanjing210096,China)

Let R be an associative ring.A left R-module M is called n-FP-injective if Ext1(N,M)=0 for any left R-module N whose FP-projective dimension≤n.As applications,some equivalences of n-FP-injective modules are given.

cotorsion theory,FP-projective dimension,n-FP-injective modules,(pre)cover

O153.3

A

1008-5513(2014)03-0286-06

10.3969/j.issn.1008-5513.2014.03.010

2013-10-30.

江蘇省研究生創(chuàng)新基金(CXLX13-072).

張齊(1983-),碩士,研究方向：代數(shù)學.

2010 MSC:16E05,16E10