汪志賓, 張 量

(安徽師范大學數(shù)學計算機科學學院,安徽蕪湖 241003)

柱面的由一些重要曲線刻畫的特征

汪志賓, 張 量

(安徽師范大學數(shù)學計算機科學學院,安徽蕪湖 241003)

通過對曲線副法線曲面的研究,得到了柱面的由一些重要曲線刻畫的特征.

柱面;副法線曲面;測地線;曲率線

1 引 言

測地線在微分幾何的研究中占有重要地位.根據(jù)測地線的定義,容易知道正則曲線α必是其副法線面Σ上的一條測地線.注意到α是直母線的一條正交軌線,自然要問:如果除α外還存在直母線的另一條正交軌線也是Σ的測地線,此時Σ有何性質(zhì).我們將證明此時Σ必為柱面.事實上,我們得到了更一般的結(jié)果.

定理1 設Σ為α的副法線面.若存在一條非直母線的測地線(C),且其上每點均沿α上對應點的副法向量方向平移常數(shù)c個單位,得到的另一曲線(C＊)也為測地線,則Σ為柱面.

由定理1可直接得到如下推論.

推論設Σ為α的副法線面.若除α外還存在直母線的一條正交軌線為測地線,則Σ為柱面.

受上述結(jié)果的啟發(fā),我們考慮對于曲率線和漸近線是否也有類似的結(jié)論.對此我們證明了下面的兩個定理.

定理2 設Σ為α的副法線面,若存在直母線的一條正交軌線為Σ的曲率線,則Σ為柱面.

定理3 設α(u)為一般螺線,即α(u)的撓率和曲率之比=c(常數(shù)),又設Σ:r(u,v)=α(u)+vB(u)為α的副法線面.若存在直母線的一條正交軌線v=b為Σ的漸近線,則或者Σ為柱面,或者α(u)的參數(shù)方程為(當τ取初值τ(0)=1時)

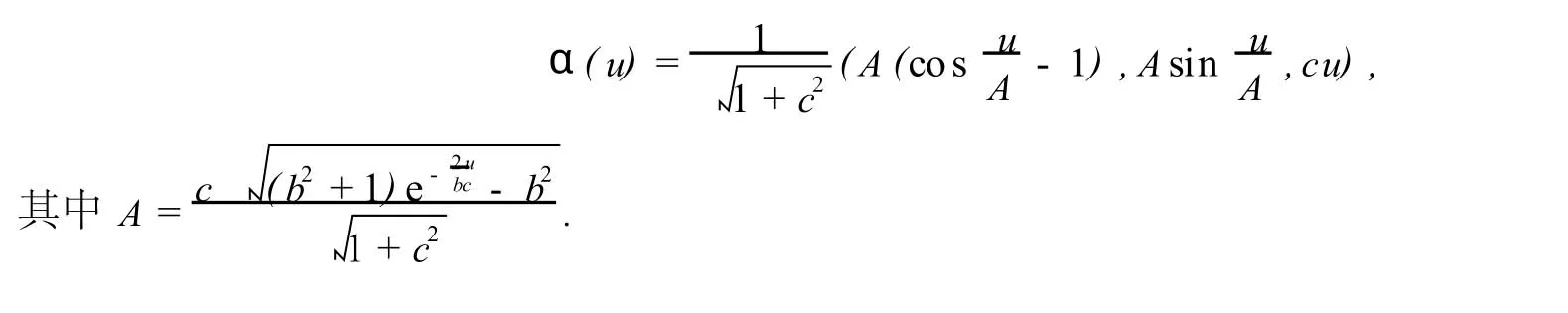
2 預備知識

設α是一條以弧長為參數(shù)的正則曲線,曲率和撓率分別為κ和τ,曲率κ恒不為零.又設T,N,B分別為α的切向量,主法向量和副法向量.考慮以α為準線,B為直母線方向向量的直紋面Σ,該直紋面稱為α的副法線曲面.其參數(shù)表示為

根據(jù)曲線的Frenet-Serret公式[1],

3 主要定理的證明

定理1的證明 設β(s)=r(u(s),v(s))=α(u(s))+v(s)B(u(s))為Σ上的測地線,則由測地線的微分方程(引理2),有

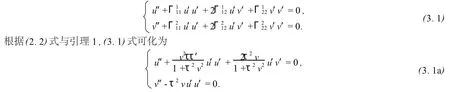
又設Σ上另一條測地線(C＊)方程為

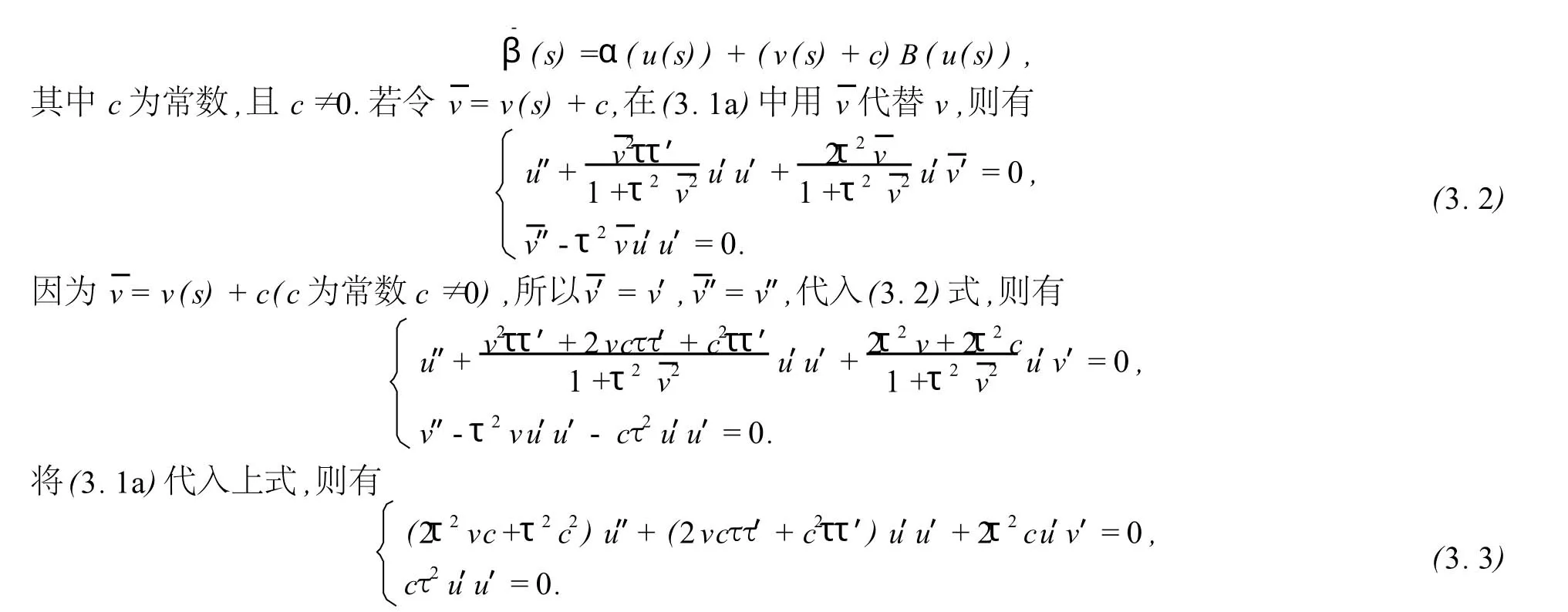
因為β(s)不為直母線,則u不為常數(shù),即u′≠0.由(3.3)的第二個方程,有τ=0,此時(3.3)的第一個方程也成立.所以α為平面曲線,則Σ為柱面.

定理2的證明 設ā(s)=r(u(s),v(s))=α(u)+v(s)B(u(s))為Σ上的曲率線,由副法線面的基本公式以及引理3得曲率線的方程為

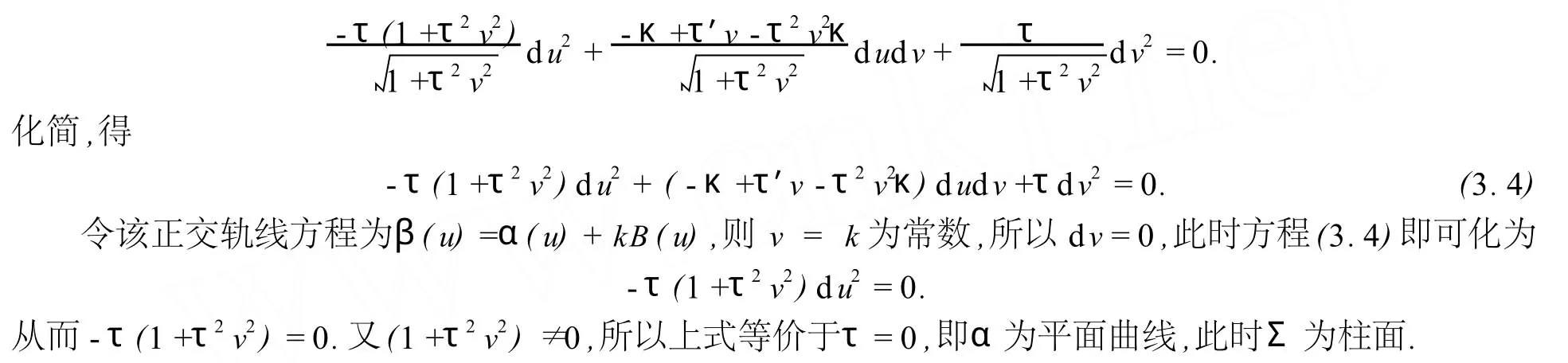
定理3的證明 因為直母線正交軌線β(u)=α(u)+bB(u)為副法線面Σ的漸近線,滿足漸近線方程(2.4),根據(jù)副法線面基本公式,有

[1] Do Carmo M.Differential geometry of curves and surfaces[M].New Jersey：Prentice-Hall,Inc.,1976：15-185.

[2] 彭家貴,陳卿.微分幾何[M].北京：高等教育出版社,2002：78-117.

[3] 梅向明,黃敬之.微分幾何[M].北京：高等教育出版社,1988：98.

[4] 沈純理,黃宣國.微分幾何[M].北京：經(jīng)濟科學出版社,1997：37-38.

Some Characterizations of Cylinders Described by Some Important Curves

WA N G Zhi-bin
(College of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)

Based on the study of the binormal surface of acurve,this paper obtains some characterizations of cylinders described by some important curves.

cylinder;binormal surface;geodesic;lines of curvature

O186.11

A

1672-1454(2011)03-0153-04

2008-06-23