倪 倩, 王旭輝

(1.南京工業(yè)大學(xué) 數(shù)理科學(xué)學(xué)院,南京 211816; 2.中國科學(xué)院 數(shù)學(xué)與系統(tǒng)科學(xué)研究院,北京 100190; 3. 河海大學(xué) 數(shù)學(xué)學(xué)院,南京 211100)

0 引 言

函數(shù)的最佳平方逼近是數(shù)值分析課程中的重要部分[1-2],該內(nèi)容也與最小二乘法緊密相連,在后續(xù)的理論分析和實(shí)際應(yīng)用中有著廣泛的用途[3].在平時(shí)的課堂教學(xué)中,通常都是將函數(shù)的最佳平方逼近問題轉(zhuǎn)換為最小二次問題進(jìn)行講解,實(shí)踐表明,這樣處理,學(xué)生不容易理解和掌握.因此,如何處理這部分內(nèi)容,便于學(xué)生理解是教師值得研究的問題.本文嘗試將向量空間投影理論[4]應(yīng)用到函數(shù)最佳逼近,最小二乘法與微分方程Galerkin方法求解問題的講解中,可使學(xué)生更加直觀地理解相關(guān)內(nèi)容,促進(jìn)學(xué)生對相關(guān)內(nèi)容的掌握和應(yīng)用,并培養(yǎng)學(xué)生融會(huì)貫通處理學(xué)習(xí)內(nèi)容的能力.

1 函數(shù)的最佳平方逼近簡介

給定函數(shù)f(x)∈C[a,b]及函數(shù)空間Φ,其中Φ由基函數(shù)φ1(x),φ2(x),…,φn(x)張成,φi(x)∈C[a,b],i=1,2,…,n.函數(shù)f(x)在空間Φ中的最佳平方逼近問題為:計(jì)算φ∈Φ使得誤差函數(shù)

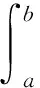
(1)

達(dá)到最小,其中ω(x)為給定的權(quán)函數(shù).

計(jì)算c1,c2,…,cn使得E(c1,c2,…,cn)達(dá)到最小,可求解下列線性方程組

(2)

上述方程組 (2) 可化簡為

(3)

2 空間投影及函數(shù)最佳平方逼近

下面引入向量的空間投影.

2.1 向量的空間投影

給定向量u∈d,d∈+及d中的子空間V,其中V由基向量v1,v2,…,vn張成.記v為u在子空間V中的投影,即v∈V且

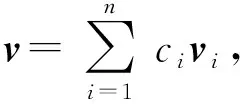
(4)

其中cT=(c1,c2,…,cn)∈n,A=(〈vi,vj〉)i,j=1,2,…,n,bT=(〈u,v1〉,〈u,v2〉,…,〈u,vn〉).又由于v1,v2,…,vn線性無關(guān),故A非奇異.此外,由 (4) 式得,E1為關(guān)于變量c1,c2,…,cn的二次函數(shù),其最小值在cT=(c1,c2,…,cn)滿足Ac=b時(shí)取得.故u在V中的投影v可表示為

v=(v1,v2,…,vn)A-1b.

上述求解過程具有直觀的幾何解釋(見圖1示意圖).

圖1 向量投影示意圖

特別地,當(dāng)v1,v2,…,vn兩兩正交時(shí),A=diag(〈v1,v1〉,〈v2,v2〉,…,〈vn,vn〉).此時(shí),u在V中的投影可表示為

2.2 空間投影與函數(shù)最佳平方逼近

對于函數(shù)的最佳平方逼近問題 (1),可借助向量的空間投影進(jìn)行處理.定義內(nèi)積

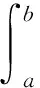
用函數(shù)空間Φ代替3.1節(jié)中向量空間V,用函數(shù)空間Φ的基函數(shù)φ1(x),φ2(x),…,φn(x)代替3.1節(jié)中的向量空間V的基,從而對于函數(shù)的最佳平方逼近問題,從空間投影的角度可建立法方程組

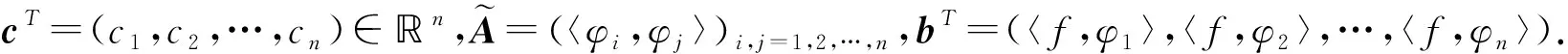
特別地,當(dāng)φ1(x),φ2(x),…,φn(x)為一組正交基,即φ1(x),φ2(x),…,φn(x)滿足

注1(最小二乘問題情形) 如果考慮最小二乘問題:給定點(diǎn)(xi,yi),權(quán)因子ωi,i=1,…,l,計(jì)算

注2(微分方程的Galerkin方法求解[5]) 如果考慮如下齊次微分方程求解問題:

(5)

可將向量空間中內(nèi)積替換成能量內(nèi)積 (Energy inner product)

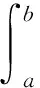
針對微分方程問題 (5), 可通過變分得到其弱形式,進(jìn)行類似推導(dǎo)可得線性方程組

(6)

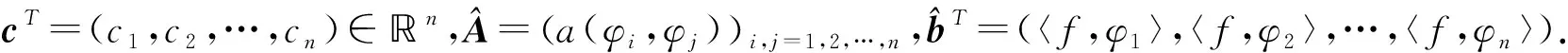
3 結(jié) 論

對于函數(shù)最佳平方逼近,利用向量空間的空間投影推導(dǎo),可將復(fù)雜的運(yùn)算轉(zhuǎn)化為學(xué)生非常熟悉的線性代數(shù)問題,而且?guī)缀我饬x非常直觀.此外,通過將相關(guān)結(jié)論推廣到最小二乘法,微分方程的Galerkin方法求解,可將這一類問題理解成最佳逼近(在某種意義下),或者是不同空間的投影.該教學(xué)內(nèi)容的相關(guān)處理,可使學(xué)生更容易掌握與應(yīng)用函數(shù)最佳逼近,最小二乘法以及微分方程Galerkin方法求解等知識(shí).相關(guān)處理方法可促進(jìn)學(xué)生在學(xué)習(xí)中提高整體把握,融會(huì)貫通的能力.

致謝作者非常感謝相關(guān)文獻(xiàn)對本文的啟發(fā)以及審稿專家提出的寶貴意見.