雙側(cè)參數(shù)假設檢驗中原假設的選擇
金百鎖
(中國科學技術(shù)大學 統(tǒng)計與金融系,合肥 230026)
0 引 言
概率論與數(shù)理統(tǒng)計是大學所有理科專業(yè)的公共必修課,很多文科專業(yè)也需要開設統(tǒng)計學這門課程.在統(tǒng)計學教學當中,最重要的是統(tǒng)計思維的訓練.美國科學院院士C.R.Rao教授認為“在理性的基礎上,所有的判斷都是統(tǒng)計學”[1],因此假設檢驗在統(tǒng)計思維訓練中占有十分重要的地位,包含了很多統(tǒng)計思想,也是當今討論最多的部分,例如2018年,72位作者一起在Nature子刊發(fā)表了一篇論文建議降低在眾多實驗中使用的顯著性水平[2],引來了87 位作者一起發(fā)表的反駁論文[3].
關于假設檢驗的一些統(tǒng)計思想在陳希孺院士的教材中有詳細的介紹[4].本文討論的假設檢驗理論是1828年發(fā)展起來的奈曼-皮爾遜假設檢驗,這一理論需要控制第一類錯誤,導致假設檢驗中的原假設和對立假設有不同的地位.因此一般的原假設設立原則,是把不希望被輕易否定的假設,或者已經(jīng)經(jīng)歷了一段時間考驗的假設,設為原假設[4].而這一原則在教材中通常只針對于單側(cè)檢驗[5-7].對于雙側(cè)參數(shù)假設檢驗,只把參數(shù)相等的假設設為原假設,而參數(shù)不等的假設設為對立假設.為什么不能把參數(shù)不相等的假設設為原假設,是因為在這個原假設下第一類錯誤不好計算嗎?這一問題在教材中解釋的并不詳盡,本文的目的是分析一下這個問題,并給出一些統(tǒng)計解釋.
1 雙側(cè)假設檢驗問題
大學的統(tǒng)計學教材,都是從正態(tài)分布總體的參數(shù)檢驗開始介紹.因此本文以正態(tài)分布總體的雙側(cè)參數(shù)假設檢驗為例.假設X1,…,Xn為獨立同分布服從正態(tài)分布N(μ,σ2),σ2已知,檢驗μ=μ0這一假設,并放在對立假設,即檢驗問題是
H0∶μ≠μ0?H1∶μ=μ0.
(1)

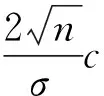
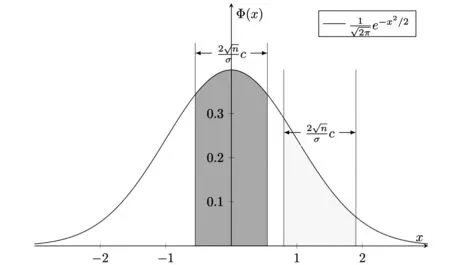
圖1 標準正態(tài)區(qū)間概率示意圖

然而在這個拒絕域的條件下,第二類錯誤為
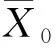
2 實 例
假設某一工廠聲稱其生產(chǎn)的一個合格的精密元件的長度服從正態(tài)分布,其均值為900mm,方差為100mm,現(xiàn)從一批元件中隨機抽取25件,測得其平均長度為901mm,試在顯著水平α=0.05下,確定這批產(chǎn)品是否合格.
解 法1建立假設
H0∶μ=900 ?H1∶μ≠900.

法2建立假設
H0∶μ≠900 ?H1∶μ=900.


3 結(jié) 論
基于上面的分析,在保證第一類錯誤小于α的條件下,對于正態(tài)總體,如果原假設是μ≠μ0,則在一次試驗中,都幾乎不可能接受μ=μ0這一對立假設,即使這一對立假設是真實成立的.其背后的原因,應該是μ=μ0這一點相對于μ的全部參數(shù)空間的取值可以忽略不記,對立假設只有一個取值μ=μ0和原假設的參數(shù)空間幾乎不可分.
上節(jié)構(gòu)造的檢驗不是好的檢驗,因為功效函數(shù)β(μ)在對立假設μ=μ0下達到最大值α,這個功效太小了.一個好的檢驗,都需要在檢驗參數(shù)遠離原假設參數(shù)空間的時候,或參數(shù)離原假設參數(shù)空間有一定距離但樣本量趨于無窮時,功效函數(shù)趨于1,而當μ=μ0作為對立假設時無法做到遠離原假設或有一定距離.
顯著性假設檢驗的目的是,通過樣本驗證是否有足夠的證據(jù)拒絕原假設.當μ≠μ0為原假設的時候,即使這個原假設不成立,通過上面的分析發(fā)現(xiàn)在正態(tài)分布總體下無法找到合適的檢驗有足夠的證據(jù)能拒絕這個原假設.因此本文的結(jié)論是μ≠μ0不能作為原假設.
推薦的解決方案是:不再強求μ=μ0,構(gòu)建一個新的檢驗,即用下式
H0∶|μ-μ0|≥Δ?H1∶|μ-μ0|<Δ,

致謝作者非常感謝相關文獻對本文的啟發(fā)以及審稿專家提出的寶貴意見,以及加拿大約克大學吳月華教授和中國科學技術(shù)大學王學欽教授提出的寶貴意見.

