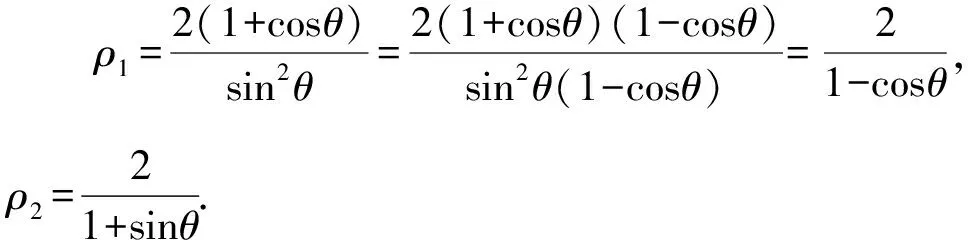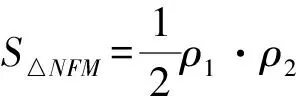何 勇

(白云興農(nóng)中學(xué),貴州 貴陽 550000)

2023年全國甲卷理科數(shù)學(xué)的解析幾何大題是非常不錯(cuò)的一道題目,該題解法多樣,可用高中的多個(gè)知識(shí)點(diǎn)進(jìn)行解答.

1 高考真題

(1)求p;

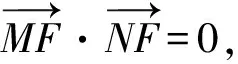
2 解法探究

2.1 第(1)問解析

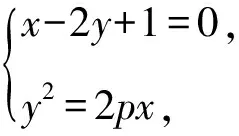
所以yA+yB=4p,yAyB=2p.

即2p2-p-6=0.

因?yàn)閜>0,解得p=2．

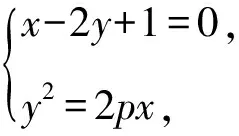
所以xA+xB=8p-2,xAxB=1.

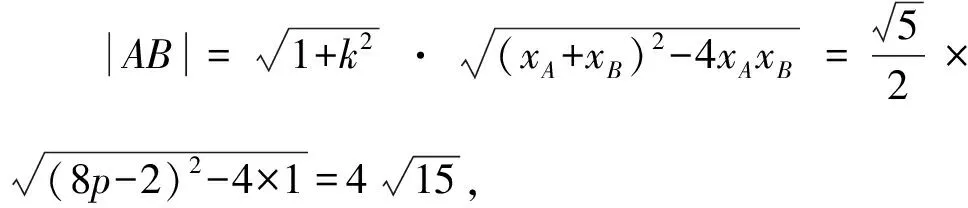
因?yàn)閜>0,解得p=2．

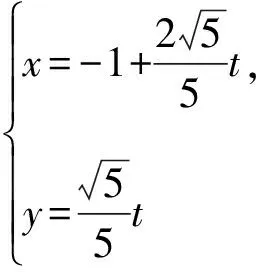
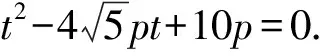
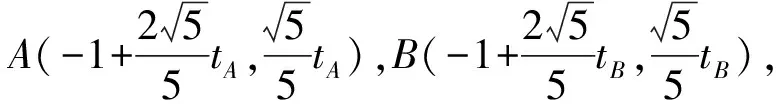
即2p2-p-6=0.因?yàn)閜>0,解得p=2．

說明直線x-2y+1=0的參數(shù)方程有無數(shù)個(gè)[1],與所取直線上的點(diǎn)有關(guān).

2.2 第(2)問解析

所以y1+y2=4m,y1y2=-4n,

△=16m2+16n>0,得m2+n>0.

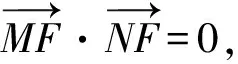
所以(x1-1)(x2-1)+y1y2=0.

即(my1+n-1)(my2+n-1)+y1y2=0.

即(m2+1)y1y2+m(n-1)(y1+y2)+(n-1)2=0.

將y1+y2=4m,y1y2=-4n代入,得

4m2=n2-6n+1,即4(m2+n)=(n-1)2>0.

所以n≠1,且n2-6n+1≥0.

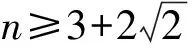
設(shè)點(diǎn)F到直線MN的距離為d,

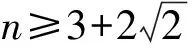
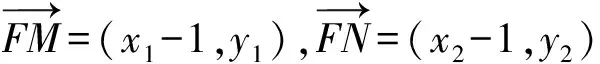
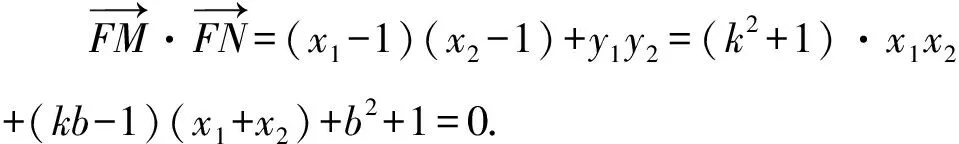
所以k2+b2+6kb-4=0.

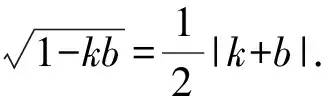
要使直線MN與拋物線有兩個(gè)交點(diǎn),則△=16-16kb>0.即kb<1.

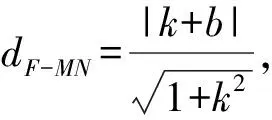
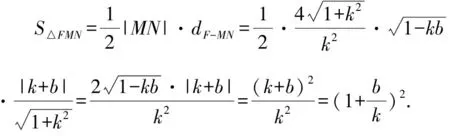
由k2+b2+6kb-4=0可得

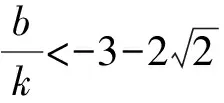
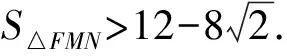
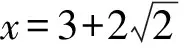
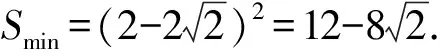
啟示解法1和解法2在設(shè)直線方程形式上是不同的,直線方程的不同導(dǎo)致計(jì)算量和思想方法不同,在教學(xué)中要重視y=kx+b與x=ky+b兩種方程的應(yīng)用,選擇合適的方程會(huì)大大減少計(jì)算量或者避免分類討論的出現(xiàn),提高解題的效率.

解法3設(shè)∠MFx=θ,由拋物線的焦半徑可得

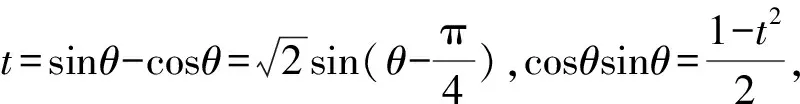
圖1 平移后拋物線示意圖

=4(-ρ2sinθ+1)