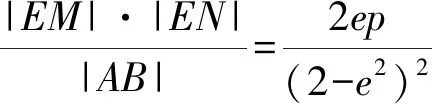劉才華

(山東省泰安市寧陽(yáng)第一中學(xué),山東 泰安 271400)

已知拋物線C的方程為y2=2px(p>0),焦點(diǎn)為F.已知點(diǎn)P在C上,且點(diǎn)P到點(diǎn)F的距離比它到y(tǒng)軸的距離大1.

(1)試求出拋物線C的方程;

這是一道高三年級(jí)模擬試題,我們通過探究,對(duì)試題作進(jìn)一步的推廣,得到圓錐曲線的弦對(duì)頂點(diǎn)張直角的一個(gè)定值性質(zhì),性質(zhì)的證明需用到如下引理:

引理1 設(shè)直線l與拋物線y2=2px(p>0)相交于A,B兩點(diǎn),則OM⊥ON(O為坐標(biāo)原點(diǎn))的充要條件是直線l過定點(diǎn)(2p,0)[1].

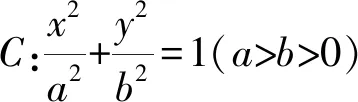
對(duì)于拋物線,我們有如下命題:

證明由題意及引理1知直線MN過定點(diǎn)E(2p,0),設(shè)過點(diǎn)E的直線方程為x=my+2p,交拋物線于M(x1,y1),N(x2,y2).

y2-2pmy-4p2=0.

則y1y2=-4p2.

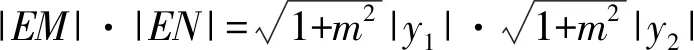
y2-2pmy-p2=0.

則y3+y4=2pm,y3y4=-p2.

=2p(1+m2).

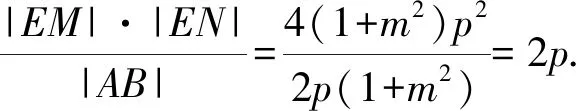
命題1得證.

對(duì)于橢圓,我們有如下命題:

(a2+b2)2(b2m2+a2)y2+2mab2(a4-b4)y-4a4b4=0.

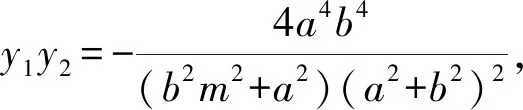
過點(diǎn)F(c,0)的直線方程為x=my+c,交橢圓于A(x3,y3),B(x4,y4).

(b2m2+a2)y2+2cmb2y-b4=0.

對(duì)于雙曲線,我們有如下命題:

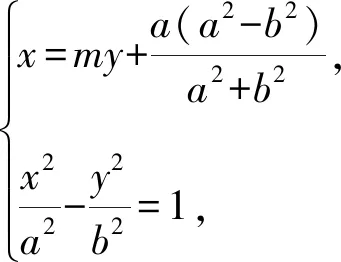
(a2+b2)2(b2m2-a2)y2+2mab2(a4-b4)y-4a4b4=0.

過點(diǎn)F(c,0)的直線方程為x=my+c,交雙曲線于A(x3,y3),B(x4,y4).

(b2m2-a2)y2+2cmb2y+b4=0.