譚暉, 肖麗鵬

( 江西師范大學數學與統(tǒng)計學院, 江西南昌 330022)

1.引言與結果

在本文中, 我們將假定讀者熟悉亞純函數的值分布理論和標準記號[1].另外, 使用記號σ(f)表示亞純函數f(z)的增長級, 且使用記號σ2(f)表示f(z)的超級[2], 定義為

考慮二階齊次線性微分方程

其中A和B是整函數, 我們知道方程(1.2)的每個解都是整函數.

則稱f是方程(1.2)的次正規(guī)解.

高仕安和蔣翼邁定義亞純函數的e-型級如下:

定義1[3]如果f(z)是亞純函數, 那么f(z)的e-型級定義為

因此, 由(1.3)和(1.4)式, 可知如果σe(f)=0, 那么f是次正規(guī)的.

顯然, 如果f(z)是整函數, 那么

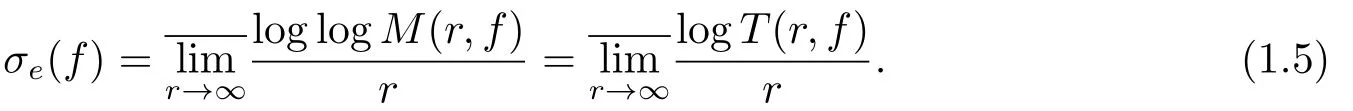
引入超級和e-型級的定義, 可以更好的判定亞純函數f的增長性, 顯然超級和e-型級有如下關系: (i)若0<σe(f)<∞, 則σ2(f)=1; (ii)若σ2(f)<1, 則σe(f)=0, 即(1.3)式成立.

但我們不能斷定當σ2(f)=1時, σe(f)>0成立.

有許多學者研究了一些特殊方程解的增長性這一方面的問題[4?8], 并得到了下面的定理.

沒有非平凡次正規(guī)解, 且其每一個非零解f滿足σ2(f)=1.

最多有1個次正規(guī)解.

(ii)方程(1.14)的所有解f滿足σ2(f)=1除去(i)中可能出現的次正規(guī)解.

下面例2-6表明在定理4-7中可能存在非平凡次正規(guī)解.

2.引理部分

引理1[4]設f是超越亞純函數且σ(f)=σ <∞, Γ ={(k1,j1),(k2,j2),··· ,(km,jm)}是由不同整數對組成的有限集, 滿足ki>ji≥0,i=1,2,··· ,m, 又設ε>0是給定的常數, 則

(i)存在零測度集E1?[0,2π), 使得如果ψ0∈[0,2π)E1, 則存在常數R0= R0(ψ0) > 0, 對滿足arg z =ψ0及|z|≥R0的所有z及對所有(k,j)∈Γ, 有

(ii)存在對數測度為有限的集合E2?(1,∞), 使得對滿足|z|E2∪[0,1] 的所有z及所有(k,j)∈Γ , 有(2.1)式成立;

(iii)存在線性測度有限集合E3?[0,∞), 使得對滿足|z|的所有z及所有(k,j)∈Γ, 有

(i)如果δ(P,θ)>0, 那么

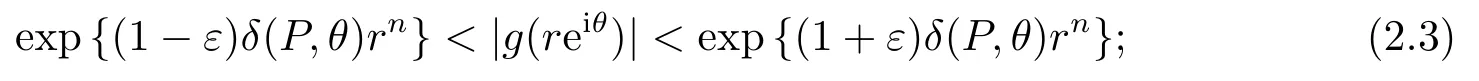
(ii)如果δ(P,θ)<0, 那么

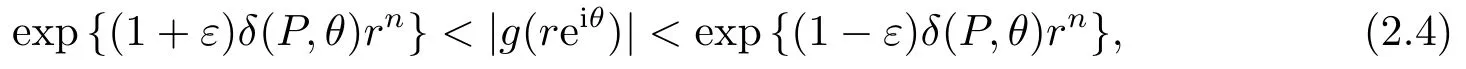
其中H2={θ ∈[0,2π);δ(P,θ)=0}是有限集.

引理3[4]設f(z)為超越亞純函數, α>1為一給定的常數, k,j為整數且滿足k >j ≥0.

(i)存在一個對數測度有限的集合E1?[1,∞)和一個常數K >0, 使得對所有滿足|z|=r[0,1]∪E1的z, 我們有

(ii)存在零測度集E2?[0,2π), 使得如果θ ∈[0,2π)E2, 則存在常數R = R(θ) > 0, 對滿足arg z =θ及|z|≥R的所有z有(2.5)式成立.

引理4[8]設A和B是有限級整函數, 如果f(z)是方程

的解, 則σ2(f)≤max{σ(A),σ(B)}.

3.定理的證明

定理1的證明首先證σ2(f) = 1.根據引理4有σ2(f) ≤max{σ(A1eaz),σ(A0ebz)} = 1, 又由定理A知σ2(f)≥1, 故σ2(f)=1.

由引理3, 可知存在一個有限對數測度的子集E ?(1,∞), 和常數B > 0滿足對所有滿足|z|=r[0,1]∪E的z, 我們有

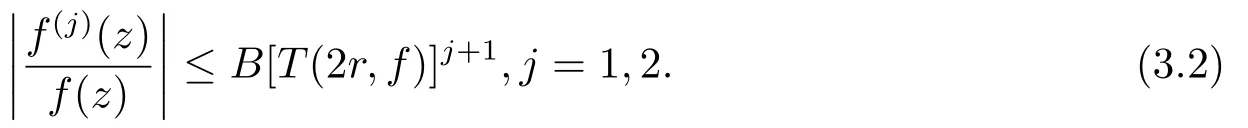
令z =reiθ, 則

分兩種情況討論:

由(1.11)和(3.1), (3.2), (3.4), (3.5)式, 可知

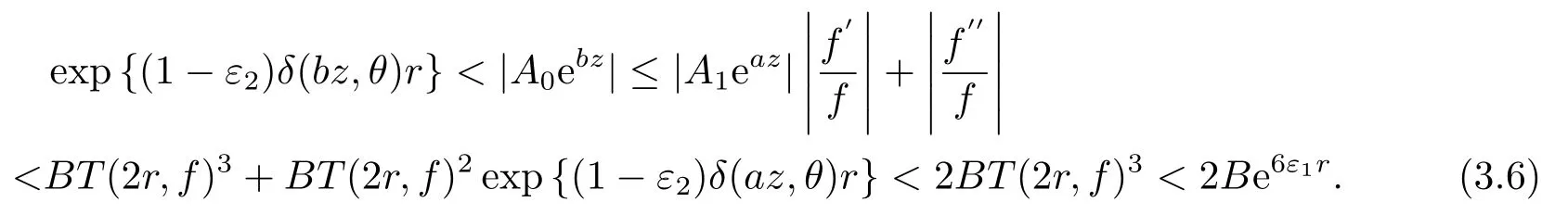
我們取0<ε2<1且0<6ε1<(1 ?ε2)δ(bz,θ), 則(3.6)式不可能成立.

2) 假設a=cb(0 0, 存在一射線arg z = θ, θ ∈[0,2π)(H1∪H2), δ(az,θ) = cδ(bz,θ) > 0.當r充分大時, 我們有

由(1.11)和(3.1), (3.2), (3.7), (3.8)式, 可知

我們取0<2ε3<0<6ε1<ε3(1+c)δ(bz,θ), 則(3.9)式不可能成立, 即矛盾.

定理2的證明(i)假設f1和f2(?)是方程(1.12)的次正規(guī)解, 則f1 ?f2(0)是方程(1.12)的對應齊次方程(1.11)的次正規(guī)解.這矛盾于定理1, 所以方程(1.12)最多有1個次正規(guī)解.

(ii)由定理1, 可知方程(1.12)的對應齊次方程(1.11)的所有解滿足σ2(f) = 1.由常數變易法, 可知方程(1.12)的所有解滿足σ2(f) ≤1.如果σ2(f) < 1, 那么f顯然滿足(1.3)式, 即f是次正規(guī)的.所以由(i), 可知方程(1.12)的所有解f滿足σ2(f)=1 除去(i)中可能出現的次正規(guī)解.

定理3的證明假設f0)是方程(1.13)的解, 則f是整函數.由于a2≤0, 先假設a2=0.

第1步 證明σ(f)=∞.如果f是非零多項式, 由引理6, 比較方程(1.13)兩邊的增長性可得矛盾, 所以方程(1.13)沒有多項式解.

由(3.11)和(3.17)式, 可得

又由(3.10)和(3.15)-(3.18)式, 可得

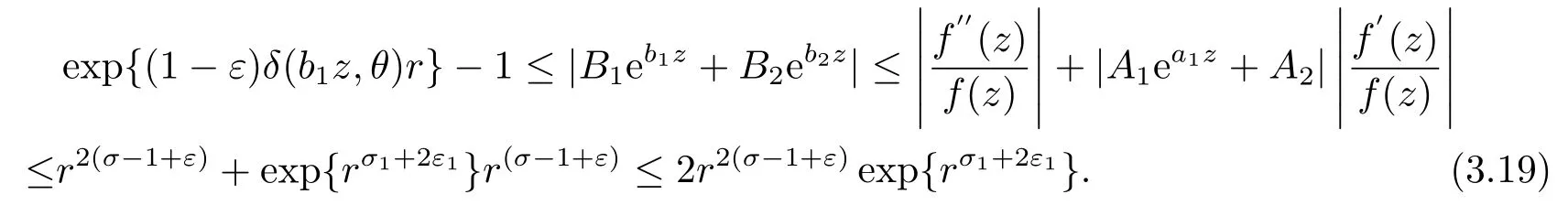
由于δ(b1z,θ)>0,0<3ε1<1 ?σ1, 可知(3.19)式是一個矛盾.

當(3.13)成立時, 用類似于上述方法, 同樣可得矛盾.

由于δ(b1z,θ)>0,0<3ε1<1 ?σ1, 可知(3.22)式是一個矛盾.

情形2 b1|a1|且θ1=π.同樣我們分成兩種情況討論.

因此,

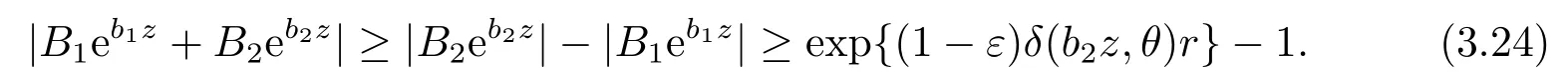
用情形1(i)的方法, 同樣可得矛盾.

由(3.11)和(3.25)式, 可得

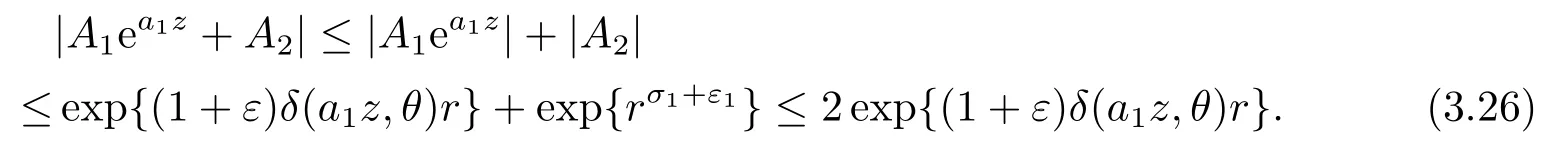
將(3.10),(3.21)和(3.26)代入(3.16)式, 可得

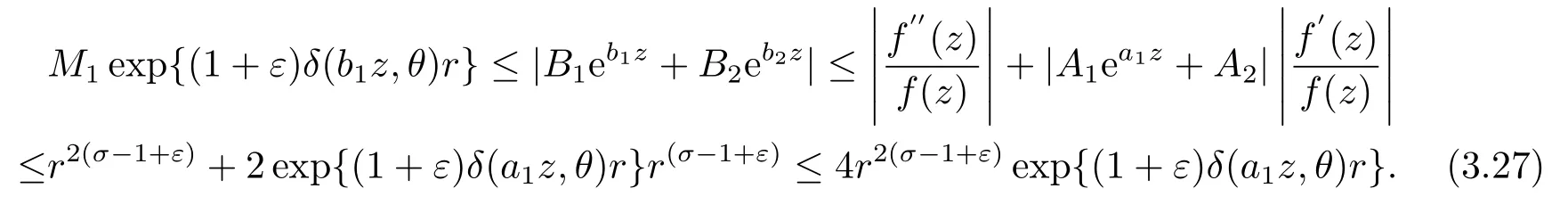
由|b1|>|a1|可知, δ(b1z,θ)>δ(a1z,θ)>0, 那么(3.27)式是一個矛盾.

綜上, 可知σ(f)=∞.

第2步 證明σ2(f) = 1.由引理4和max{σ(A1ea1z+A2),σ(B1eb1z+B2eb2z)} = 1, 可知σ2(f)≤1.

根據引理3, 可知存在一個有限對數測度的子集E1?(1,∞)和常數B > 0滿足對所有滿足|z|=r0,1]∪E1的z, 我們有

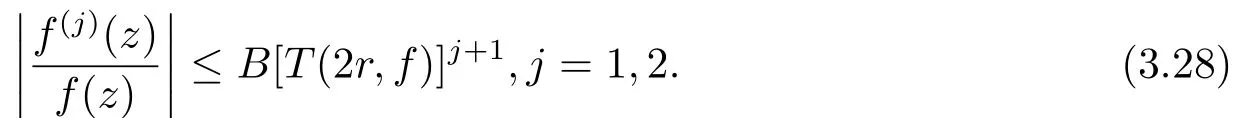
由M1> 0, |b1| > |a1|可知, δ(b1z,θ) > δ(a1z,θ) > 0, 又根據超級的定義和引理7可知,σ2(f)≥1.所以σ2(f)=1.

綜上, 可知σ2(f)=1.

第3步 證明方程(1.13)沒有非平凡次正規(guī)解.如果f是方程的非平凡次正規(guī)解, 則f滿足(1.3)式, 即對任意給定的ε2>0, 有

對于第1步中的情形1和情形2的(i), 我們有(3.30)式成立.由(3.30)和(3.32)式, 可得

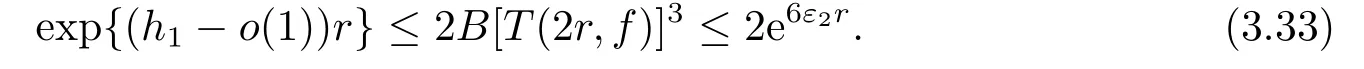
對于第1步情形2中的(ii), 我們有(3.31)式成立.由(3.31)和(3.32)式, 可得

綜上, 可知方程(1.13)沒有非平凡次正規(guī)解.

當a2<0時, 可令a1≤a2<0, 使用類似于上面的證法, 可完成定理3的證明.

定理4的證明使用與定理2相同的證法.

定理5的證明(i)運用注2, 類似于定理3的證法; (ii)-(iii)使用與定理2相同的證法.

定理6的證明(i)假設f0)是方程(1.15)的解, 則f是整函數.由ak≤0(k =2,3,··· ,n),可分成兩種情形討論.

情形1 a2,a3,··· ,an都為零, 即ak=0(k =2,3,··· ,n), 類似于定理3的證明.

第1步 證明σ(f)=∞.如果f是非零多項式, 由引理6, 比較方程(1.15)兩邊的增長性可得矛盾, 所以方程(1.15)沒有多項式解.

又由(3.10),(3.15),(3.36)和(3.37)式, 可得

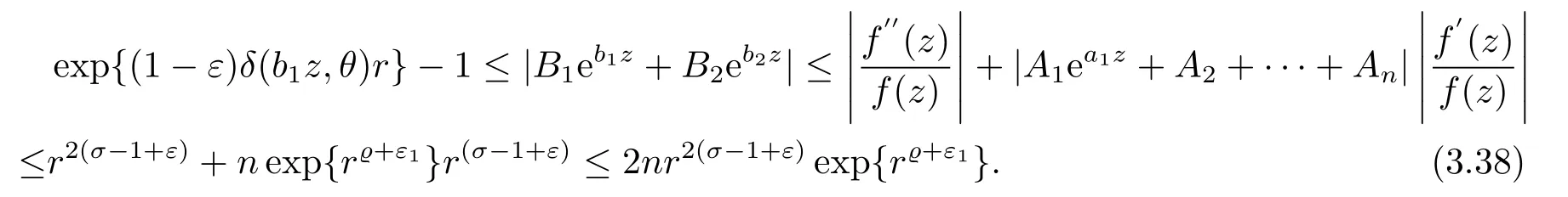
由于δ(b1z,θ)>0,0<3ε1<1 ??, 可知(3.38)式是一個矛盾.

當(3.13)成立時, 用類似于上述方法, 同樣可得矛盾.

由|b1|>|a1|可知, δ(b1z,θ)>δ(a1z,θ)>0, 又M1>0, 那么(3.41)式是一個矛盾.

綜上, 可知σ(f)=∞.

第2步 證明σ2(f)=1.由引理4和max{σ(A1ea1z+A2+···+An),σ(B1eb1z+B2eb2z)}=1,可知σ2(f)≤1.

由M1> 0, |b1| > |a1|可知, δ(b1z,θ) > δ(a1z,θ) > 0, 又根據超級的定義和引理7可知,σ2(f)≥1.所以σ2(f)=1.

綜上, 可知σ2(f)=1.

第3步 證明方程(1.15)沒有非平凡次正規(guī)解.如果f是方程的非平凡次正規(guī)解, 則f滿足(1.3)式, 即對任意給定的ε2>0, 有

對于第1步中的情形1.1和情形1.2的1), 我們有(3.42)式.由(3.42)和(3.44)式, 可得

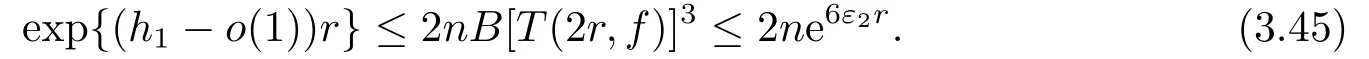
對于第1步情形1.2中的2), 我們有(3.43)式成立.由(3.43)和(3.44)式, 可得

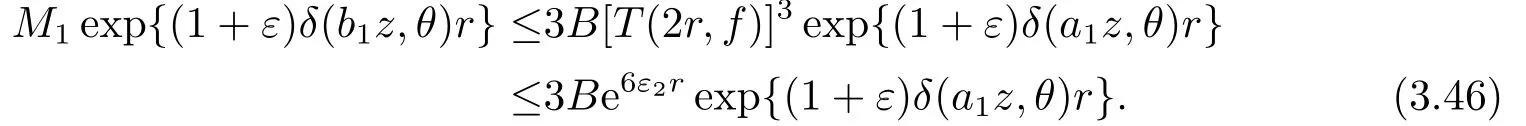
綜上, 可知方程(1.15)沒有非平凡次正規(guī)解.

情形2 a2,a3,··· ,an至少有一個不為零.不失一般性假設a2<0, 可令a1

(ii)使用與定理2相同的證法.

定理7的證明(i)運用注2, 類似于定理6的證法.(ii)使用與定理2相同的證法.