王定宇, 周少波

(1.華中科技大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 湖北武漢 430074;2.密歇根大學(xué)統(tǒng)計(jì)學(xué)系, 密歇根安娜堡 48104)

1.引言

長(zhǎng)期以來(lái)傳染病的傳播和流行給人類健康帶來(lái)了極大威脅, 例如曾在中世紀(jì)流行于歐洲的黑死病, 如今的新型冠狀病毒肺炎等, 都對(duì)人類的健康和經(jīng)濟(jì)的發(fā)展帶來(lái)了負(fù)面的影響.為研究1665-1666年的黑死病在英國(guó)倫敦的流行規(guī)律以及1906年瘟疫在印度孟買的流行規(guī)律,Kermack和McKendrick在1927年首先建立了SIR倉(cāng)室傳染病模型[1].他們的工作為SIR模型的建立奠定了基礎(chǔ).SIRS和SEIR等傳染病模型都是在SIR模型的基礎(chǔ)上提出來(lái)的.SIR模型的具體數(shù)學(xué)表達(dá)形式如下

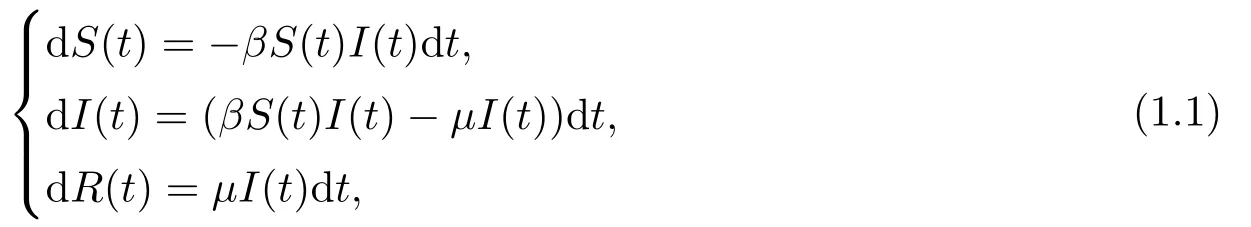
其中S(t)表示易感者(Susceptible), I(t)表示患病者(Infectious), R(t)表示康復(fù)者(Recovered),β表示日接觸率, μ表示日恢復(fù)率.

由于人類對(duì)某些疾病的免疫時(shí)間是有限的, 若考慮康復(fù)者會(huì)重新轉(zhuǎn)換成易感者喪失免疫力, 人們提出了如下SIRS模型

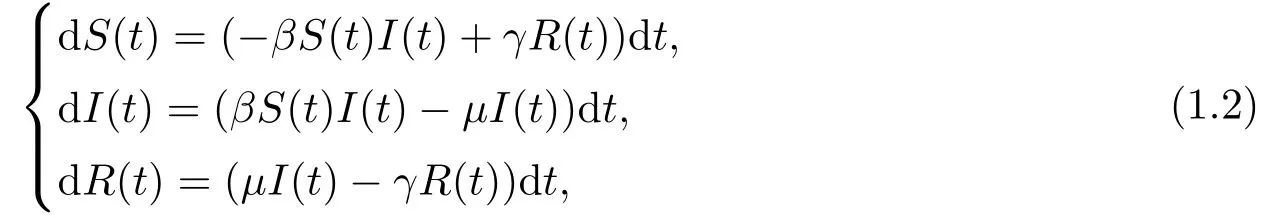
其中γ表示喪失免疫率.

由于現(xiàn)代人對(duì)疾病防控意識(shí)的增強(qiáng), 心理作用在傳染病治愈過(guò)程中的作用越來(lái)越明顯.同時(shí)在絕大多數(shù)傳染病模型動(dòng)力學(xué)分析的文獻(xiàn)中, 都只考慮了系統(tǒng)內(nèi)總?cè)丝诤愣ǖ奶厥馇闆r.因此朱晶[2]假定系統(tǒng)內(nèi)總?cè)丝诘脑鲩L(zhǎng)符合Logistic人口增長(zhǎng)模型, 提出了如下基于心理作用的SIR傳染病模型

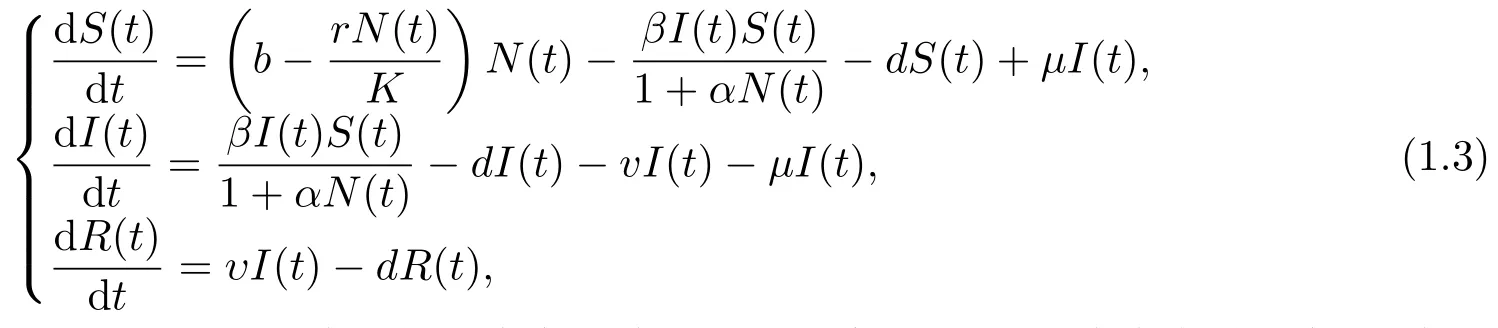
其中N(t)為t時(shí)刻的人口總量; b為自然出生率; d為自然死亡率; r =b ?d為內(nèi)稟增長(zhǎng)率; K為環(huán)境容納量; α為心理作用系數(shù)(即采取相應(yīng)的預(yù)防控制措施影響發(fā)病率), 且假設(shè)1/K < α < 1;β為傳染率; μ為自然恢復(fù)率; υ為獲得終身免疫率.除內(nèi)稟增長(zhǎng)率r以外的所有參數(shù)均為正常數(shù),參數(shù)r的大小由自然出生率b和自然死亡率d共同決定.證明了當(dāng)閾值<1時(shí), 疾病將會(huì)消亡;當(dāng)閾值>1時(shí), 疾病將會(huì)持久存在.

顯然, 在模型(1.3)中, 當(dāng)心理作用系數(shù)α的數(shù)值相對(duì)較大時(shí), 單位時(shí)間內(nèi)由易感者轉(zhuǎn)換成感染者的人數(shù)會(huì)降低, 傳染病的傳染將會(huì)得到抑制; 當(dāng)α的數(shù)值較小時(shí), 單位時(shí)間內(nèi)會(huì)有更多的易感者轉(zhuǎn)換成感染者, 則傳染病的傳染趨勢(shì)將會(huì)擴(kuò)大.因此, 心理作用系數(shù)α將會(huì)對(duì)疾病的傳播趨勢(shì)產(chǎn)生深刻的影響.

基于此, 李文軒等人[3?5]提出了人口增長(zhǎng)滿足Logistic方程的基于心理作用的SIRS模型

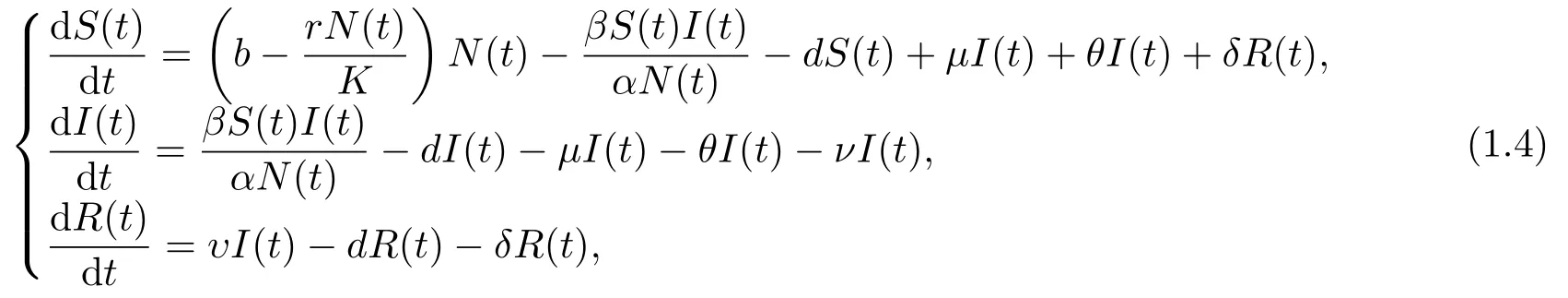
其中θ表示治愈率; δ表示喪失免疫率; υ表示獲得暫時(shí)免疫率.

實(shí)際上, 我們?cè)谶M(jìn)行參數(shù)估計(jì)(如β)時(shí)會(huì)不可避免的存在一些誤差, 即參數(shù)β的估計(jì)通常是“均值”+“誤差項(xiàng)”, 若假定誤差項(xiàng)服從正態(tài)分布, 并將其標(biāo)準(zhǔn)偏差看作是噪聲強(qiáng)度, 且該噪聲強(qiáng)度可能依賴于易感人群S(t)及染病人群I(t), 則β可由β+σ ˙ B(t)替代, σ >0代表噪聲強(qiáng)度,=dB(t)/dt為白噪聲(即B(t)是布朗運(yùn)動(dòng)).因而(1.4)相應(yīng)的隨機(jī)擾動(dòng)模型為

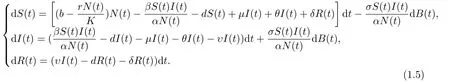
將模型(1.5)中的三個(gè)方程相加有

因此模型中的總?cè)丝谠鲩L(zhǎng)滿足Logistic方程.

近些年來(lái), 許多學(xué)者研究了類似的隨機(jī)擾動(dòng)傳染病模型[6?7].杜金姬等[6]研究了一類具有l(wèi)ogistic增長(zhǎng)的隨機(jī)SIRS傳染病模型, 證明了模型具有唯一的全局正解并指出模型的正解是穩(wěn)定的馬爾可夫過(guò)程, 同時(shí)也給出使模型中疾病滅絕的充分條件.朱玲等[7]建立了一類具有Logistic增長(zhǎng)的隨機(jī)SIVR傳染病模型, 證明了隨機(jī)系統(tǒng)正解的存在唯一性, 討論了隨機(jī)模型的解在與其對(duì)應(yīng)的確定性模型的無(wú)病平衡點(diǎn)附近的漸近行為, 并指出白噪聲強(qiáng)度σi對(duì)隨機(jī)系統(tǒng)的影響, 認(rèn)為易感者人數(shù)變化所受到隨機(jī)擾動(dòng)的強(qiáng)度σ1會(huì)對(duì)整個(gè)隨機(jī)系統(tǒng)產(chǎn)生決定性的作用.

本文將通過(guò)構(gòu)造Lyapunov函數(shù), 利用It?o引理, 強(qiáng)大數(shù)定理和停時(shí)等隨機(jī)分析理論證明模型(1.5)全局正解的存在唯一性, 并給出使疾病滅絕和持久的充分條件.其次, 本文將考慮時(shí)滯對(duì)系統(tǒng)(1.5)的影響, 證明基于心理作用的時(shí)滯隨機(jī)SIRS傳染病模型全局正解的存在唯一性.最后將應(yīng)用Euler方法和Milstein方法進(jìn)行數(shù)值模擬, 驗(yàn)證本文建立的結(jié)論并進(jìn)行分析.

2.基于心理作用的隨機(jī)SIRS傳染病模型

進(jìn)而

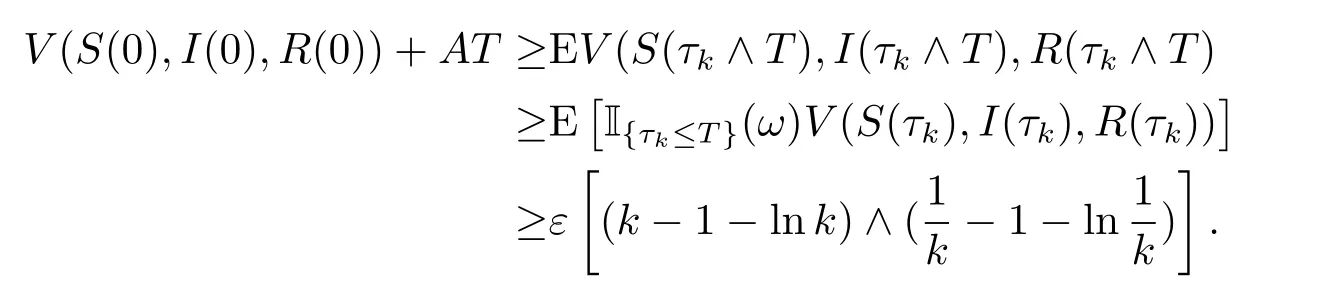
令k →∞, 有∞> V(S(0),I(0),R(0))+AT = ∞.由此出現(xiàn)矛盾, 假設(shè)不成立.因此有τ∞=∞ a.s., 從而τe=∞ a.s.證畢.

Ⅱ 滅絕性

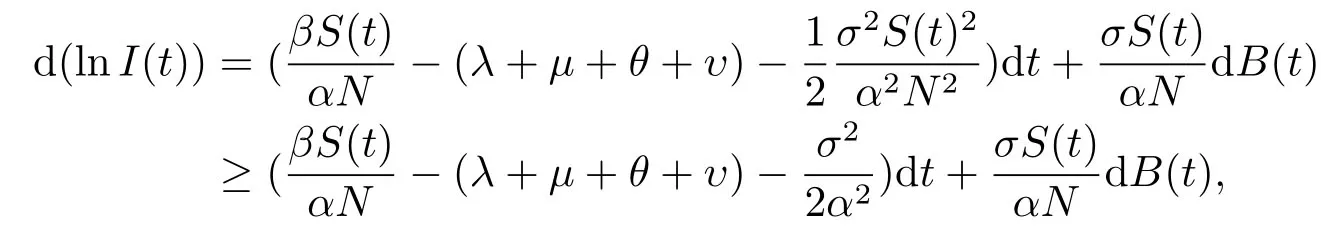
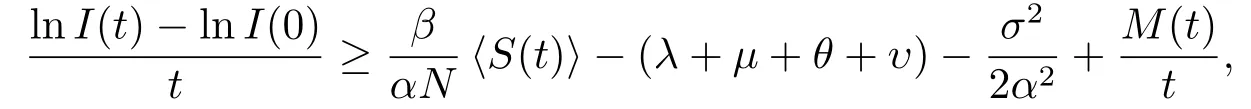
其中

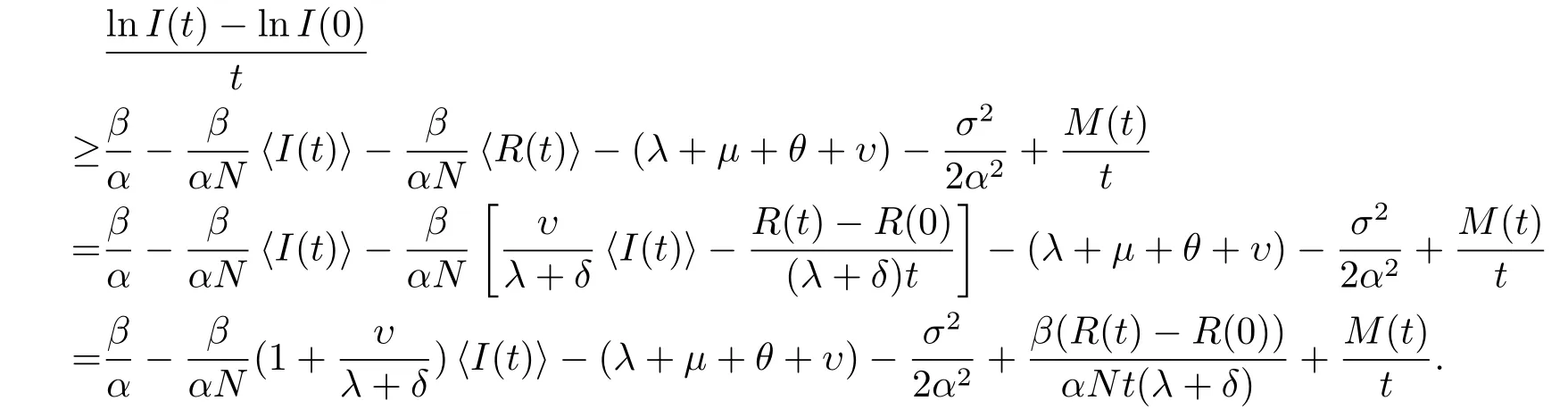
于是

其中ηj是相互獨(dú)立且服從標(biāo)準(zhǔn)正態(tài)分布N(0,1)的隨機(jī)變量.

相應(yīng)的, 系統(tǒng)(1.5)對(duì)應(yīng)的Milstein高階近似解Sj,Ij,Rj滿足如下方程組:

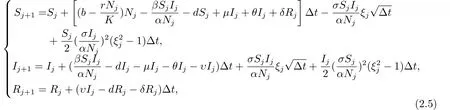
其中ξj是相互獨(dú)立且服從標(biāo)準(zhǔn)正態(tài)分布N(0,1)的隨機(jī)變量.

若取初始時(shí)刻易感者人數(shù)250萬(wàn)人, 感染者人數(shù)150萬(wàn)人, 免疫者人數(shù)5萬(wàn)人, 即S(0) =250,I(0) = 150,R(0) = 5; 取傳染率β = 0.05, 自然出生率b = 0.5, 環(huán)境容納量K = 500, 心理作用系數(shù)α = 0.1, 自然死亡率d = 0.2, 自然恢復(fù)率μ = 0.05, 治愈率θ = 0.2, 喪失免疫率δ =0.01, 獲得暫時(shí)免疫率υ =0.1, 隨機(jī)擾動(dòng)σ =0.02.由于

?0.001=2α[β ?α(d+μ+θ+υ)]<σ2=0.004<βα=0.005,

因此在該參數(shù)下系統(tǒng)存在唯一的全局正解且滿足定理2.2的條件.又由定理2.2易得?0.07 < 0 a.s.故疾病最終將會(huì)以指數(shù)形式滅亡.同時(shí)通過(guò)計(jì)算可得= 0.873 < 1.圖1中數(shù)值模擬的結(jié)果映證了此時(shí)疾病將會(huì)滅絕.

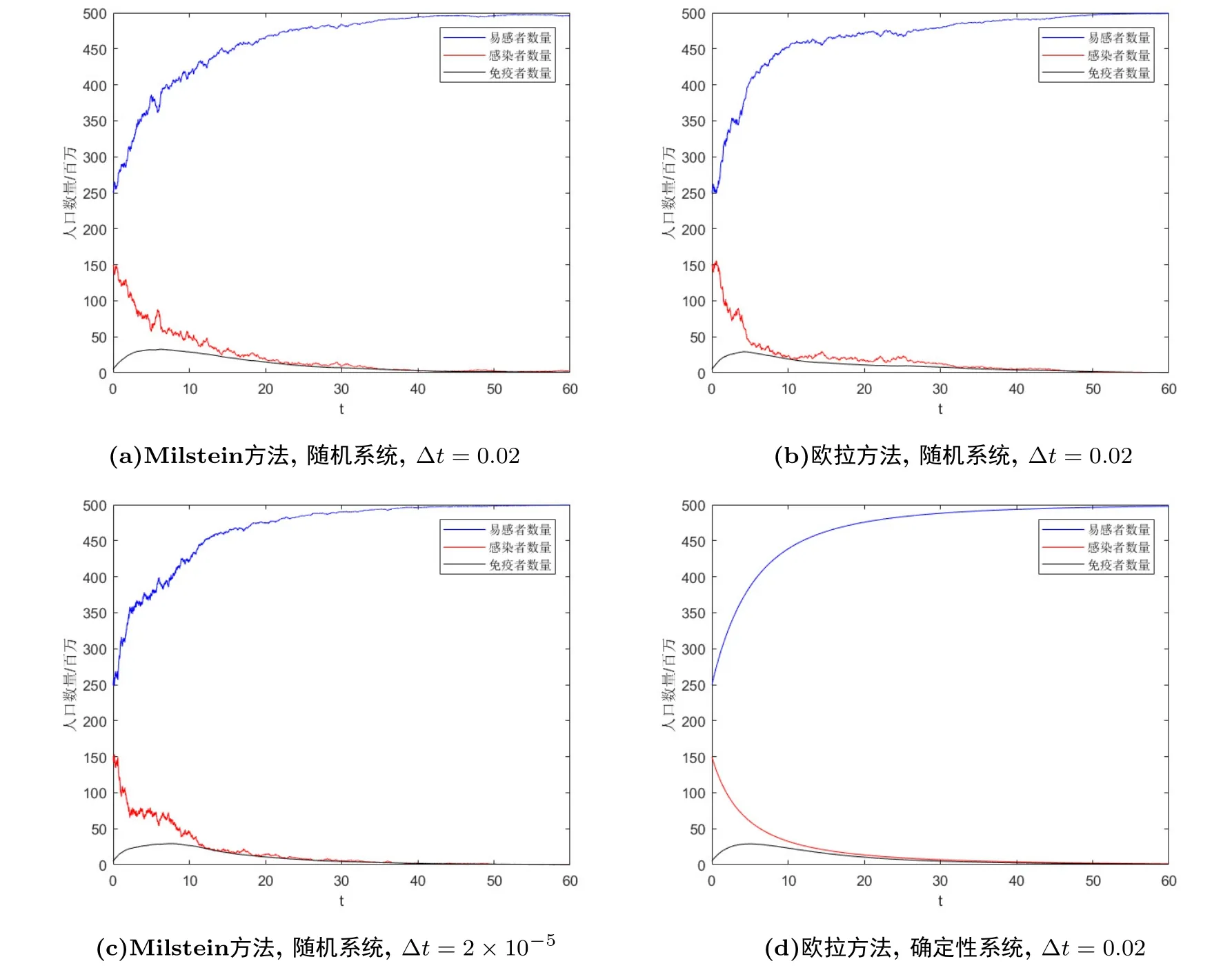
圖1 σ =0.02,<1時(shí)的數(shù)值模擬圖

相反的, 若提高傳染率β = 0.1, 降低心理作用系數(shù)α = 0.05, 保持模型中的其他參數(shù)不變,則由計(jì)算可得

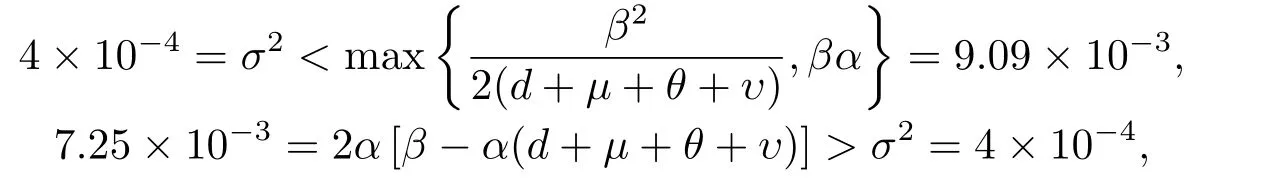
圖2展示了此時(shí)的數(shù)值模擬結(jié)果, 表明此時(shí)疾病不再滅絕而是持久存在的.

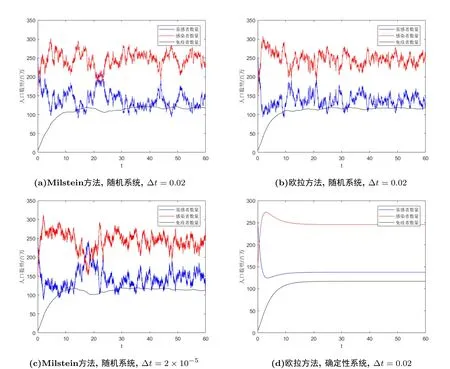
圖2 σ =0.02,>1時(shí)的數(shù)值模擬圖

更進(jìn)一步, 若保持模型中參數(shù)不變, 僅將σ增大至0.1, 經(jīng)計(jì)算可得

在某些情況下, 隨機(jī)性模型中數(shù)值模擬的結(jié)果顯示疾病將會(huì)滅亡, 但在其對(duì)應(yīng)的確定性模型中數(shù)值模擬的結(jié)果顯示疾病將會(huì)持續(xù).因此隨機(jī)擾動(dòng)會(huì)對(duì)模型產(chǎn)生極大的影響.相比于確定性系統(tǒng)(2.2), 隨機(jī)系統(tǒng)(1.5)中疾病滅絕的條件會(huì)相對(duì)弱.因此當(dāng)系統(tǒng)(1.5)中的參數(shù)可以使疾病滅絕時(shí), 同樣的參數(shù)并不一定能保證系統(tǒng)(2.2)中的疾病滅絕.數(shù)值模擬圖3(d)刻畫(huà)了這一現(xiàn)象.

圖3 σ =0.1,<1時(shí)的數(shù)值模擬圖

值得注意的是步長(zhǎng)?t的取值會(huì)對(duì)系統(tǒng)解的路徑產(chǎn)生影響.當(dāng)步長(zhǎng)?t = 2 × 10?5時(shí),S(t),I(t),R(t)的波動(dòng)要比步長(zhǎng)?t = 0.02時(shí)更加顯著.這說(shuō)明越小的步長(zhǎng)越能反應(yīng)出在一個(gè)細(xì)微的時(shí)間段內(nèi)系統(tǒng)解的變化情況, 而較大的步長(zhǎng)可能會(huì)掩蓋了在該時(shí)間段內(nèi)系統(tǒng)解的某些顯著變化.因此在計(jì)算機(jī)算力允許的條件下, 我們應(yīng)該盡可能地選擇較小的步長(zhǎng)?t.這在處理白噪聲強(qiáng)度σ值較大的隨機(jī)微分系統(tǒng)時(shí)更加的重要, 因?yàn)檩^大的σ值會(huì)使系統(tǒng)的擾動(dòng)更加的劇烈.最后通過(guò)比較不難發(fā)現(xiàn)歐拉方法與Milstein方法在處理這類隨機(jī)微分方程的效果上并沒(méi)有顯著的差異, 也沒(méi)有出現(xiàn)系統(tǒng)解不收斂的情況.而在確定性系統(tǒng)中, 由于白噪聲強(qiáng)度σ = 0, 因此Milstein方法退化成為歐拉方法, 故在這類系統(tǒng)中這兩種方法的遞推式是一樣的.

3.基于心理作用的時(shí)滯隨機(jī)SIRS傳染病模型

由于大部分傳染性疾病具有潛伏期, 因此當(dāng)易感者被傳染而轉(zhuǎn)換成感染者之后并不會(huì)馬上具有傳染性.故在t時(shí)刻受到感染的易感者并不是被t時(shí)刻的感染者感染的, 而實(shí)際上是被t ?τ時(shí)刻的感染者所感染的, 只是t ?τ時(shí)刻的感染者在(t ?τ)時(shí)刻沒(méi)有表達(dá)出傳染性.這體現(xiàn)了疾病傳染的滯后性.在具有時(shí)滯的系統(tǒng)中, 時(shí)滯可能會(huì)影響到系統(tǒng)的穩(wěn)定性, 引發(fā)系統(tǒng)的周期震蕩, 因此時(shí)滯隨機(jī)微分方程的動(dòng)力學(xué)行為會(huì)更加復(fù)雜.考慮系統(tǒng)(1.5)具有時(shí)滯的情況,建立模型如下

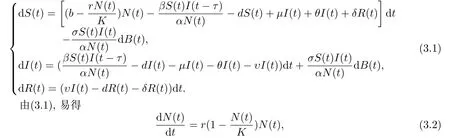
且S(t)=N(t)?I(t)?R(t), 因此可以考慮上述方程組的等價(jià)模型

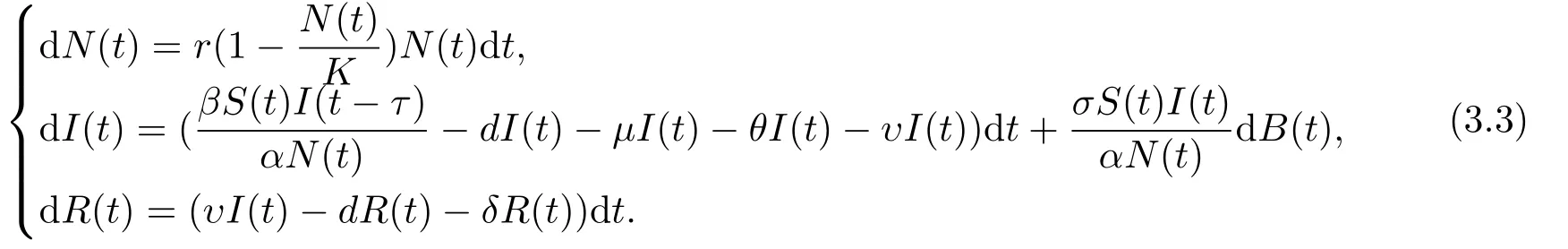
本節(jié)將證明系統(tǒng)(3.3)具有唯一的全局正解, 并繪制S(t),I(t),R(t)在不同時(shí)滯τ下對(duì)應(yīng)的路徑圖.

Ⅰ 正解的存在性和唯一性

可以計(jì)算

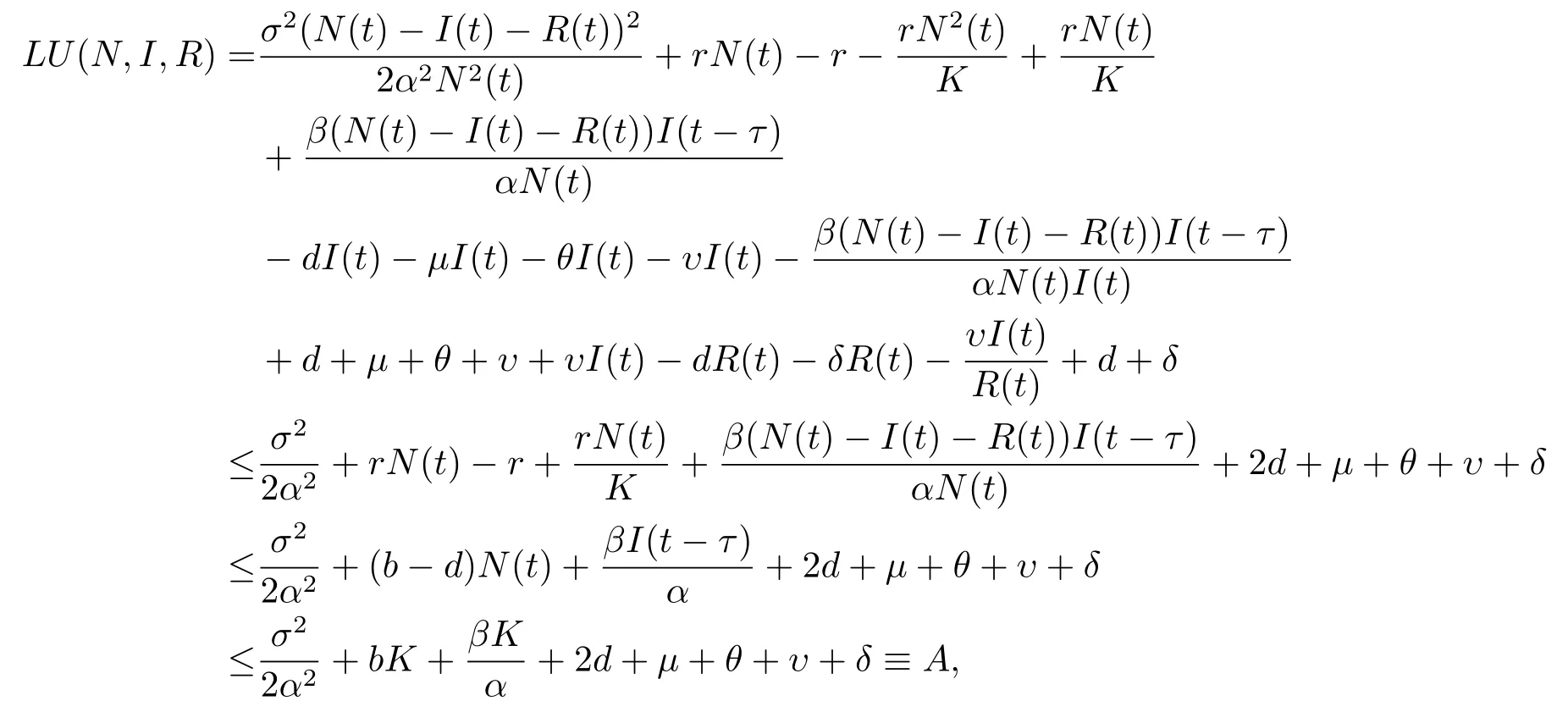
其中A是獨(dú)立于N,I,R,t的正常數(shù).因此

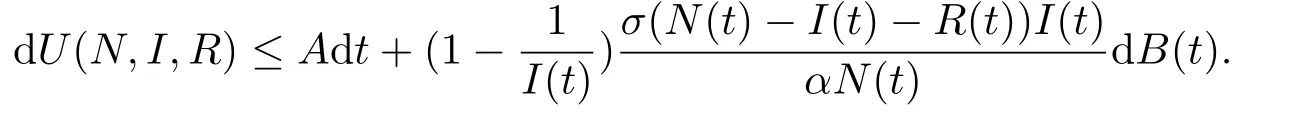
對(duì)上式兩端從0到τk∧T積分, 并取期望可得

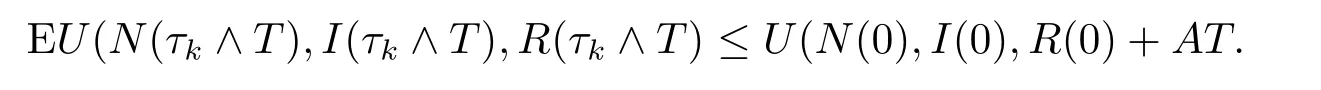
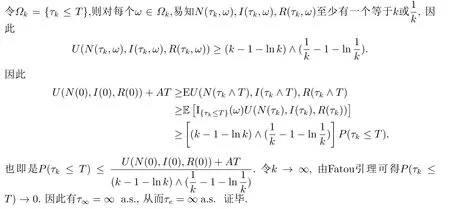
Ⅱ 數(shù)值模擬

在這一部分我們將使用高階Milstein方法對(duì)系統(tǒng)的解進(jìn)行模擬分析.

取初始時(shí)刻易感者人數(shù)250萬(wàn)人, 感染者人數(shù)150萬(wàn)人, 免疫者人數(shù)5萬(wàn)人, 即S(0) =250,I(0) = 150,R(0) = 5; 取傳染率β = 0.05, 自然出生率b = 0.5, 環(huán)境容納量K = 500,心理作用系數(shù)α = 0.1, 自然死亡率d = 0.2, 自然恢復(fù)率μ = 0.05, 治愈率θ = 0.2, 喪失免疫率δ =0.01, 獲得暫時(shí)免疫率υ =0.1, 隨機(jī)擾動(dòng)σ =0.03, 分別取不同的τ值.則系統(tǒng)(3.1)的模擬結(jié)果如圖4所示.

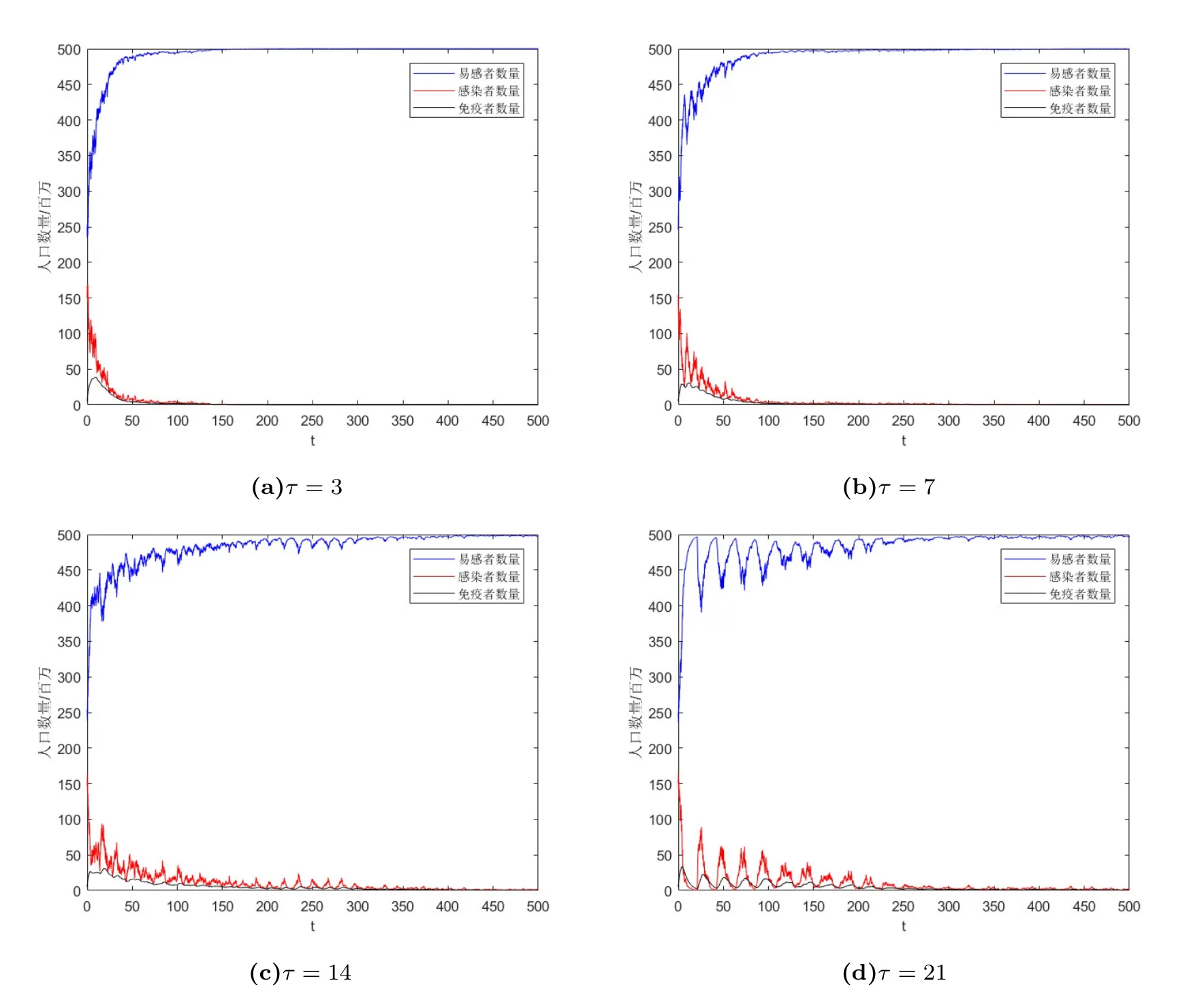
圖4 T =500,?t=0.02時(shí)的數(shù)值模擬圖

可以看到疾病最終都將滅絕.但疾病滅絕所需要的時(shí)間隨著時(shí)滯τ的增大而增大, 這說(shuō)明當(dāng)傳染病的潛伏期較長(zhǎng)時(shí), 疾病往往需要更長(zhǎng)的時(shí)間才能夠滅絕.因此具有潛伏期的疾病將會(huì)更加的狡猾, 需要政府采取更長(zhǎng)時(shí)間的隔離措施才能夠有效地預(yù)防疾病的傳播.COVID-19就具有較長(zhǎng)的潛伏期, 我國(guó)政府也是根據(jù)該傳染病的這種特性制定了入境人員14+7+7天的隔離措施, 收到了較好的成效.圖4的(c)和(d)反映出感染者和易感者人數(shù)的變化具有波動(dòng)性, 且振蕩頻率隨著時(shí)滯τ的增大而增大.這說(shuō)明當(dāng)疾病的潛伏期較長(zhǎng)時(shí), 疾病的變化趨勢(shì)是具有波動(dòng)性的, 即疫情會(huì)出現(xiàn)反復(fù), 這提醒決策部門(mén)在分析疫情時(shí)不能盲目樂(lè)觀, 要考慮到這樣的波動(dòng)特性, 做好打持久戰(zhàn)的準(zhǔn)備, 時(shí)刻緊繃, 防患未然.COVID-19在我國(guó)的傳染趨勢(shì)就具有這樣的波動(dòng)性.復(fù)旦大學(xué)附屬華山醫(yī)院感染科主任張文宏也曾在2020年接受采訪的時(shí)候表示要做好應(yīng)對(duì)疫情反復(fù), 甚至是第二波疫情的準(zhǔn)備.

4.結(jié)論

本文研究了一類具有心理作用的隨機(jī)SIRS傳染病模型的動(dòng)力學(xué)性質(zhì), 即模型解的存在唯一性, 滅絕性以及持久性.證明了當(dāng)系統(tǒng)的白噪聲強(qiáng)度較大或閾值≤1且白噪聲強(qiáng)度不大時(shí), 疾病將會(huì)滅絕; 當(dāng)閾值> 1時(shí), 對(duì)應(yīng)系統(tǒng)的解將會(huì)持續(xù).本文還研究了時(shí)滯對(duì)模型的影響.同時(shí), 我們應(yīng)用歐拉方法和Milstein高階法模擬了不同參數(shù)下S(t),I(t),R(t)的路徑圖, 證實(shí)了本文建立的結(jié)論.