李文東

(廣東省中山市中山紀念中學(xué))

含有參數(shù)的函數(shù)問題一般采用分類討論或者分離參數(shù)的方法解決,但是在一些問題中無法分離參數(shù)或者分類討論往往很復(fù)雜,這時我們可以根據(jù)條件將問題中的參數(shù)進行代換,有時能夠起到簡化的效果.

1 參數(shù)代換在函數(shù)零點問題中的應(yīng)用

例1設(shè)函數(shù)f(x)＝－x2＋ax－a(a∈R),若函數(shù)f(x)的圖像與x軸有且只有1個交點,求a的取值范圍.

由題意得f′(x)＝x2－2x＋a,則Δ＝4－4a.當Δ≤0,即a≥1時,f′(x)≥0在R上恒成立,故f(x)在R上單調(diào)遞增,因為f(0)＝－a＜0,f(3)＝2a＞0,所以函數(shù)f(x)的圖像與x軸有且只有1個交點.

當Δ＞0,即a＜1時,f′(x)＝0有2個不相等的實根,設(shè)為x1,x2(x1＜x2),則x1＋x2＝2,x1x2＝a.當x＜x1時,f′(x)＞0,函數(shù)f(x)在(－∞,x1)上單調(diào)遞增,當x1＜x＜x2時,f′(x)＜0,函數(shù)f(x)在(x1,x2)上單調(diào)遞減,當x＞x2時,f′(x)＞0,函數(shù)f(x)在(x2,＋∞)上單調(diào)遞增.因為a＝－x21＋2x1,所以函數(shù)f(x)的極大值

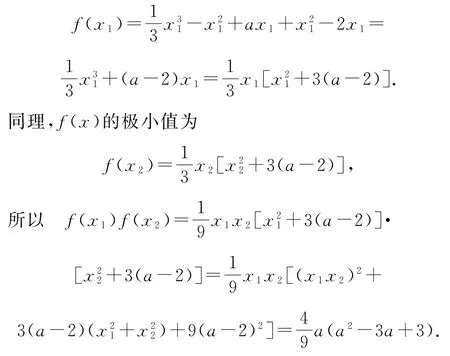
令f(x1)f(x2)＞0,解得a＞0,且當0＜a＜1時,f(0)＝－a＜0,f(3)＝2a＞0,函數(shù)f(x)的圖像與x軸有且只有1個交點.

綜上,a的取值范圍為(0,＋∞).

解法中采用參數(shù)a的局部代換,主要是方便計算,也可全部代換得到f(x1)＝3),再利用根與系數(shù)的關(guān)系,計算稍顯復(fù)雜.當然本題也可以利用多項式除法將f(x1)化簡,也可以采用分離參數(shù)的方法求解,讀者不妨試一試.

例2已知函數(shù)f(x)＝ax2－x－ln(ax)(a≠0,a∈R),討論函數(shù)f(x)的零點個數(shù).

當a＞0時,f(x)＝ax2－x－ln(ax)的定義域為(0,＋∞),f′(x)＝.令2ax2－x－1＝0,易知該方程有兩個根x1,x2且x1＜0＜x2,結(jié)合f′(x)的圖像可知f(x)在(0,x2)上單調(diào)遞減,在(x2,＋∞)上單調(diào)遞增,由于2ax22－x2－1＝0且x2＞0,于是a＝則

當a＜0時,f(x)＝ax2－x－ln(ax)的定義域為(－∞,0),且

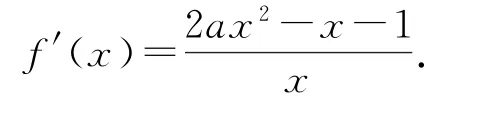
綜上,當a＜0或a＝1時,函數(shù)f(x)有1個零點,0＜a＜1或a＞1時,函數(shù)f(x)有2個零點.

由于f(x)＝ax2－x－ln(ax)中的參數(shù)a分布在兩個部分,直接分離參數(shù)求解比較困難,因此可以考慮分類討論研究函數(shù)f(x)的單調(diào)性來求解,這需要計算函數(shù)f(x)在極值點處的函數(shù)值,可以利用參數(shù)代換簡化計算結(jié)果.當a＞0時,根據(jù)題中的分析可以求得x2＝,于是

然后需要考慮其符號,求解就比較復(fù)雜.

2 參數(shù)代換在極值點偏移問題中的應(yīng)用

例3已知函數(shù)f(x)＝lnx－ax有2個不同的零點x1,x2(x1＜x2).

(1)求實數(shù)a的取值范圍;

(2)求證:x1＜

令h(t)＝e＋tlnt－2t(t∈(1,e)),則h′(t)＝lnt－1＜0,h(t)在(1,e)上單調(diào)遞減,從而h(t)＞h(e)＝0,所證成立.

例4已知函數(shù)f(x)＝x－lnx－a有2個相異零點為x1,x2(x1＜x2).

(1)求a的取值范圍;

(2)求證:x1＋x2＜

(1)a的取值范圍為(1,＋∞)(求解過程略).

(2)可知0＜x1＜1＜x2.由于a＝x1－lnx1,要證x1＋x2＜只需證

根據(jù)零點的含義有x1－lnx1＝a＝x2－lnx2,可實現(xiàn)參數(shù)a的代換.

3 參數(shù)代換在恒成立問題中的應(yīng)用

例5設(shè)函數(shù)f(x)＝x2－8x＋alnx(a∈R),若函數(shù)f(x)有2個極值點x1,x2(x1＜x2)且x1≠1,總有＞t(4＋3x1－x21)成立,求t的取值范圍.

當t≥0時,g′(x)＞0,g(x)在(0,2)上單調(diào)遞增且g(1)＝0,故當1＜x＜2時,g(x)＞0,不符合題意.

當t＜0 時,令h(x)＝tx2＋2x＋t.當Δ＝4－4t2≤0,即t≤－1時,g′(x)≤0,g(x)在(0,2)上單調(diào)遞減且g(1)＝0,故當0＜x＜1時,g(x)＞0;當1＜x＜2時,g(x)＜0,符合題意;當－1＜t＜0時,注意到h(0)＝t＜0,h(1)＝2(t＋1)＞0,則存在x0∈(0,1),使得h(x0)＝0,且當x∈(x0,1)時,g′(x)＞0,g(x)在(x0,1)上單調(diào)遞增且g(1)＝0,故當x0＜x＜1時,g(x)＜0,不符合題意.

綜上,t的取值范圍為(－∞,－1].

4 參數(shù)代換在求最值問題中的應(yīng)用

例6設(shè)函數(shù)f(x)＝xex－alnx.當a＞0時,函數(shù)f(x)的最小值為g(a),求g(a)的最大值.

f(x)＝xex－alnx,由于a＞0,f′(x)＝(x＋1)ex－,f″(x)＝(x＋2)ex＋＞0,故f′(x)在(0,＋∞)上單調(diào)遞增,且limx→0＋f′(x)＝－∞,f′(a)＝(a＋1)ea－1＞0,故對每一個a＞0,必存在唯一的正數(shù)x0,使得f′(x0)＝(x0＋1)ex0－0,即x0(x0＋1)ex0＝a,函數(shù)f(x)在(0,x0)上單調(diào)遞減,在(x0,＋∞)上單調(diào)遞增,故g(a)＝fmin(x)＝f(x0)＝x0ex0－alnx0＝x0ex0－x0(x0＋1)ex0lnx0.

令h(x)＝xex－x(x＋1)exlnx,則h′(x)＝－ex[(x＋1)2＋x]lnx,令h′(x)＞0,得0＜x＜1,函數(shù)h(x)在(0,1)上單調(diào)遞增,令h′(x)＜0,得x＞1,故函數(shù)h(x)在(1,＋∞)上單調(diào)遞減,故gmax(a)＝hmax(x)＝h(1)＝e,此時a＝2e.

求g(a)＝x0ex0－alnx0的最大值,這是參數(shù)a的函數(shù),但是x0(x0＋1)ex0＝a中無法求出x0,因此利用參數(shù)代換進行求解.

(完)