Xing-Bo Pan(潘興博) Xiu-Bo Chen(陳秀波) Gang Xu(徐剛)Zhao Dou(竇釗) Zong-Peng Li(李宗鵬) and Yi-Xian Yang(楊義先)

1Information Security Center,State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China

2School of Information Science and Technology,North China University of Technology,Beijing 100144,China

3Huawei Technologies Co. Ltd,Shenzhen 518129,China

4School of Computer Science,Wuhan University,Wuhan 430072,China

Keywords: quantum nondemolition measurement, special single particle basis, quantum network coding,quantum multicast communication

1. Introduction

In 2000,Ahlswedeet al.[1]proposed the idea of classical network coding for the first time, which is of epoch-making significance and brings new opportunities for the development of information communication.

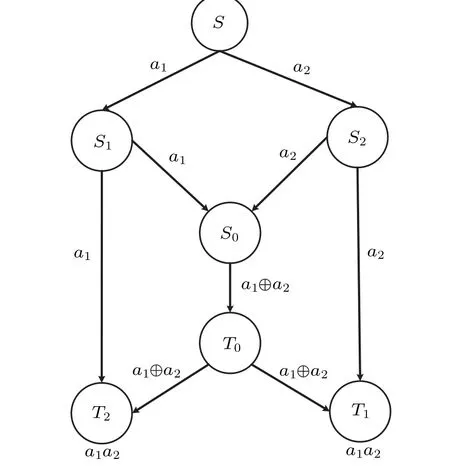
Fig.1. Classic network coding.

As shown in Fig.1, by performing an XOR operation at the bottleneck node,the receiversT1andT2can get bitsa1anda2simultaneously. The protocol completes two pairs of multicast communication over the butterfly network. The network coding solves the congestion problem at the bottleneck node,and improves the transmission efficiency and the total network throughput.[2-6]

In 2007, Hayashiet al.[7]initiated proposed a quantum network coding protocol considering the advantages of network coding. As shown in Fig. 2, sendersS1andS2transmit pure states, while receivers receive the mixed states. Although this protocol can achieve quantum 2-pair multi-unicast communication, and the fidelity of the output states cannot reach 1. It is impossible in principle to replicate exactly an unknown quantum state due to the non-cloning theorem.[8]Subsequently, Kobayashiet al.[9-11]showed that as long as classical communication is free over the butterfly network,the perfect transmission of quantum states[12-15]can be completed. This result provides a theoretical basis for perfect quantum network coding.[12,16-19]So far, a large number of quantum network coding schemes[20-24]have been proposed,some of which have been implemented in experiments.[25,26]In Ref.[25],Luet al.have demonstrated Hayashi’protocol[12]by employing eight photons generated via spontaneous parametric down-conversion. The average fidelities of cross state transmission and cross entanglement distribution achieved exceed the theoretical upper bounds permitted without prior entanglement. In Ref. [26], Pathumsootet al.have completed a particular implementation of quantum network coding using measurement-based quantum computation on IBM Q processors. Pathumsootet al. have demonstrated how a quantum computer can be used to model an entangling quantum network and experimentally confirmed the operation of quantum network coding in a superconducting device. This shows that it has taken a step from the theory of quantum network coding toward practical use on real devices. At present, quantum network coding in the form of quantum multi-unicast communication[12,16-24]emerges in endlessly,while quantum network coding in the form of quantum multicast communication[27-30]is relatively less.

Fig.2. Quantum network coding with universal cloning.

In 2006, Shi and Soljanin[27]began to study the multicast problem in quantum networks. Through quantum lossless compression and decompression technology, quantum multicast communication can be completed in quantum networks. In 2009, Liet al.[28]proposed a new optimization quantum-inspired evolutionary algorithm (QEA) to solve the multicast routing problems. In 2010, Xinget al.[29]proposed an improved quantum-inspired evolutionary algorithm for coding resource optimization based network coding multicast scheme. In 2015,Xuet al.[30]proposed a quantum cooperative multicast coding scheme. In Ref.[30],Xuet al. gave the explicit definition of quantum cooperative multicast, and designed an efficient scheme for cooperative multicast of twolevel quantum states over the butterfly network.Quantum multicast communication solves the one-to-many quantum communication problem,which is a great significance to the practical application of quantum communication networks[31-35]in the future.

We study quantum network coding and quantum multicast communication. In Ref.[36],Liet al. designed universal quantum operations by applying local operation and classical communication,[38]and proposed a perfect quantum multipleunicast network coding protocol. In Ref. [37], Pati proposed assisted cloning and orthogonal complementing of unknown quantum state. Without violating the quantum non-cloning theorem,by applying quantum non-demolitional measurement(QND),[39-41]the assisted clone and orthogonal complementation of an unknown quantum state can be achieved with the help of the quantum and classical channels. Subsequently, a number of perfect assisted cloning schemes[42-44]have been proposed.

In this paper,we propose a quantum multicast communication with network coding, which achieves quantum 2-pair multicast communication over the butterfly network. Then we extend quantum 2-pair multicast communication to the extended butterfly network,and quantumk-pair multicast communication is proposed over the extended butterfly network.Firstly,an EPR state is shared between each adjacent repeater of butterfly network, and use the quantum operations introduced in Subsection 2.1 to generate entanglement relationship between non-adjacent senders and receivers. Secondly, after each sender adds auxiliary particles according to the multicast numberk,the added auxiliary particles and the EPR state form a multi-particle entangled state through controlled NOT gates.Thirdly,we use Bell basis and single-particle basis to measure multi-particle entangled state, in which Bell basis measurement is quantum non-demolition measurement.Finally,by designing encoding and decoding strategies, quantum multicast communication can be completed with the help of classical and quantum channels.

2. Preliminaries

2.1. Quantum complementary state

In our scheme,Victor prepares an arbitrary quantum state|ψ〉v=α|0〉v+β|1〉v,whereα=cos(θ/2),β=eiφsin(θ/2),just like representing an arbitrary quantum state on the bloch sphere. The normalization condition|α|2+|β|2=1 is satisfied. We define that|ψ⊥〉vis quantum complementary state of|ψ〉v,in which|ψ⊥〉v=α|1〉v-β*|0〉v.

In order to achieve quantum multicast communication,Victor needs to perform the special single particle basis. We assume the special single particle basis{|m〉,|n〉}is

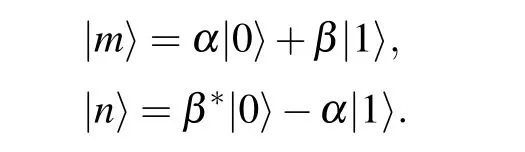
The normalization and orthogonalization relationships are satisfied between the set of basis.

2.2. Quantum operations

We refer to the encoding and decoding operations in Refs.[21,36]to design quantum operations over the extended butterfly network. The extended butterfly network is shown in Fig.3.

Fig.3. The extended butterfly network.

Fig. 4. One source node to multiple target nodes: EPR pairs are shared between a source node and multiple target nodes, Connection operation Con→n2,...,mk→nk is applied as shown in Table 1.

Table 1. Con→n2,...,mk→nk.

Table 1. Con→n2,...,mk→nk.

1 Quantum repeater Si performs CNOTm1m2,...,CNOTm1 mk successively.2 Quantum repeater Si uses {|0〉,|1〉} to measure particles m2,...,mk and let g=(g2,...,gk)be measurement result,where gi ∈{0,1}.3 Quantum repeater Si sends g2,...,gk to quantum repeater Tj (2 ≤j ≤k)through the classic channel,if g j (2 ≤j ≤k)=1,then Tj applies an X to particle nj.Here,the particles m1,m2,...,mk are owned by quantum repeater Si;the particles n1,n2,...,nk are owned by quantum repeater Tj,respectively;and X is Pauli operator.

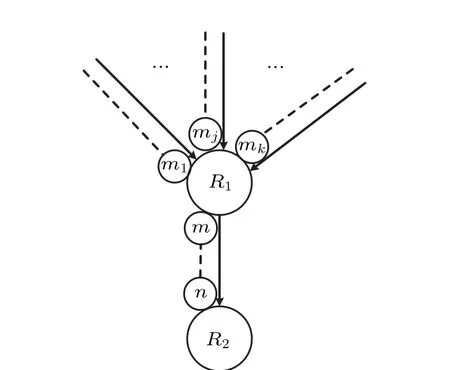
Fig.5. Multiple sources node to intermediate node: EPR pairs are shared between multiple source nodes and an intermediate node,Connection operationis applied as shown in Table 2.

Table 2.

Table 2.

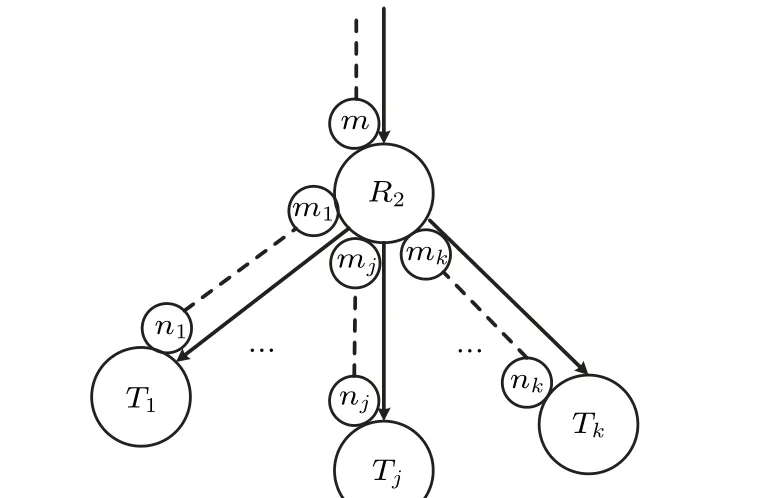
Fig.6. Intermediate node to multiple target nodes: EPR pairs are shared between an intermediate node and multiple target nodes,Connection operation Con→n1,m2→n2,...,mk→nk is applied as shown in Table 3.

Table 3. Con→n1,m2→n2,...,mk→nk.

Table 3. Con→n1,m2→n2,...,mk→nk.

1 Quantum repeater R2 performs CNOTmm1,CNOTmm2,...,CNOTmmk successively.2 Quantum repeater R2 uses {|0〉,|1〉} to measure particles m1,m2,...,mk and let g=(g1,g2,...,gk)be measurement result,where gi ∈{0,1}.3 Quantum repeater R2 sends g1,g2,...,gk to quantum repeater Tj(1 ≤j ≤k) via classic channel, if gj (1 ≤j ≤k)=1, then Tj applies an X to particle n j.Here,the particles m,m1,m2,...,mk are owned by quantum repeater R2;the particle n j is owned by quantum repeater Tj (1 ≤j ≤k); and X is the Pauli operator.

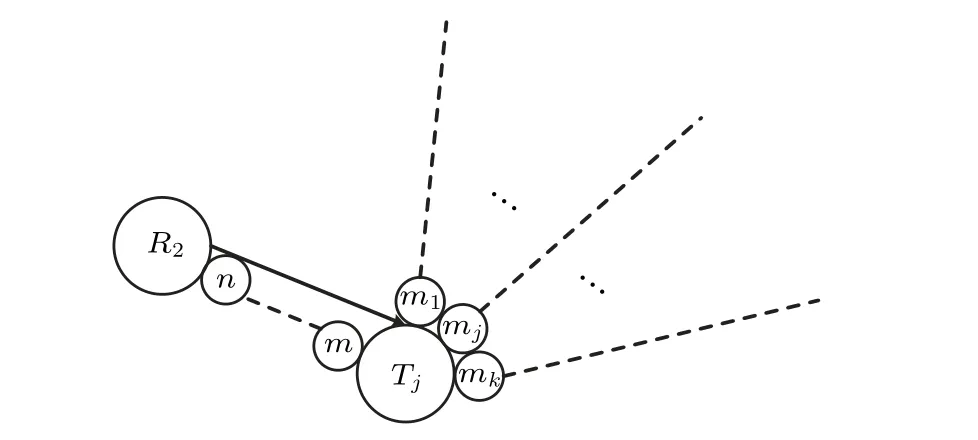
Fig. 7. Intermediate node to one target node: an EPR pair is shared between an intermediate node and a target node, Controlled-NOT gateis applied as shown in Table 4.

1 An XOR operationm1⊕m2⊕...⊕mkis performed to get classical resultλat quantum repeaterTj.

2. A controlled Not gateCNOTλmis performed at quantum repeaterTj,

whereλis the control qubit andmis the target qubit.

Here,the particlesm,m1,m2,...,mkare owned by quantum repeaterTj;the particlenis owned by quantum repeaterR2.

Fig.8. Remove operation: delete the extra particles through Remove operation Reml→n as shown in Table 5.

Table 5. Reml→n.

Through the above connection (Figs. 4-7) and remove(Fig. 8) operations, the entanglement relationship can be established in the first step of our scheme.

3. Our works

3.1. Quantum 2-pair multicast communication

We propose a quantum 2-pair multicast communication scheme over the butterfly network. As shown in Fig. 9,Victor V prepares two arbitrary quantum states|ψ1〉1=α1|0〉1+β1|1〉1,|ψ2〉2=α2|0〉2+β2|1〉2, sends|ψ1〉1toS1and|ψ2〉2toS2. Whereα1= cos(θ1/2),α2= cos(θ2/2),β1= eiφ1sin(θ1/2),β2= eiφ2sin(θ2/2). It satisfies the normalization condition|α1|2+|β1|2=1,|α2|2+|β2|2=1. On the butterfly network, we allow either one qubit transmission in quantum channel or no more than two-bit classical communication in classical channel. Our scheme is divided into four stages: establishing entanglement relationship, adding auxiliary particles, quantum measurements and encoding process,and transmission and decoding process.

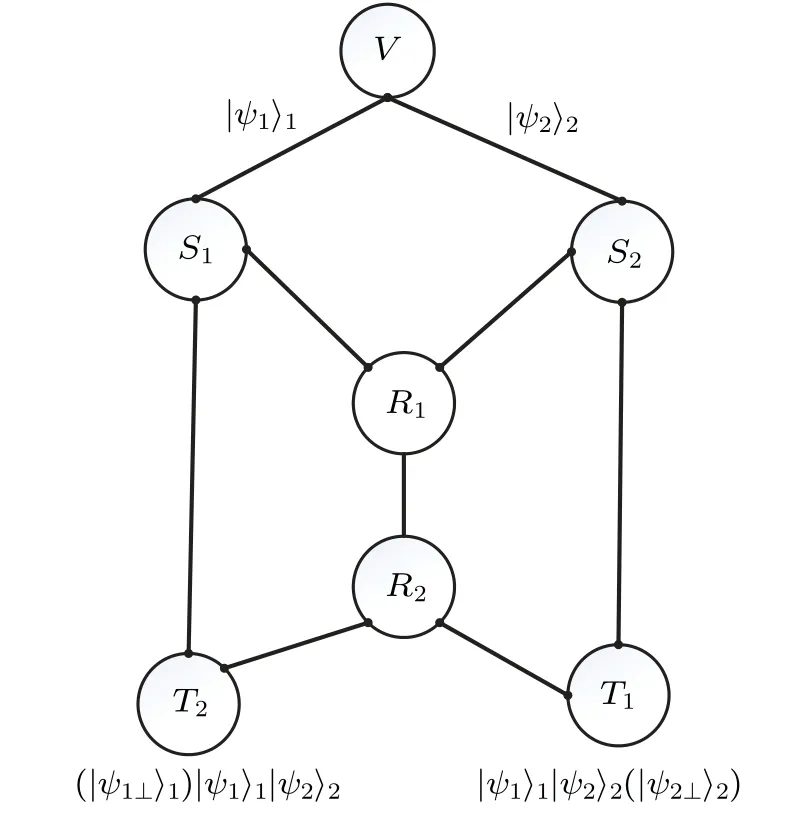
Fig.9. The butterfly network with preparer.

Secondly,adding auxiliary particles. In our scheme,auxiliary particles are added according to the multicast numberk. The number of auxiliary particles is (k-2)×2. According to the formula, there is no need to add auxiliary particles for quantum 2-pair multicast communication. Go directly to quantum measurements and encoding process. It should be noted that quantum 2-pair multicast communication is the only case which no auxiliary particles are added.

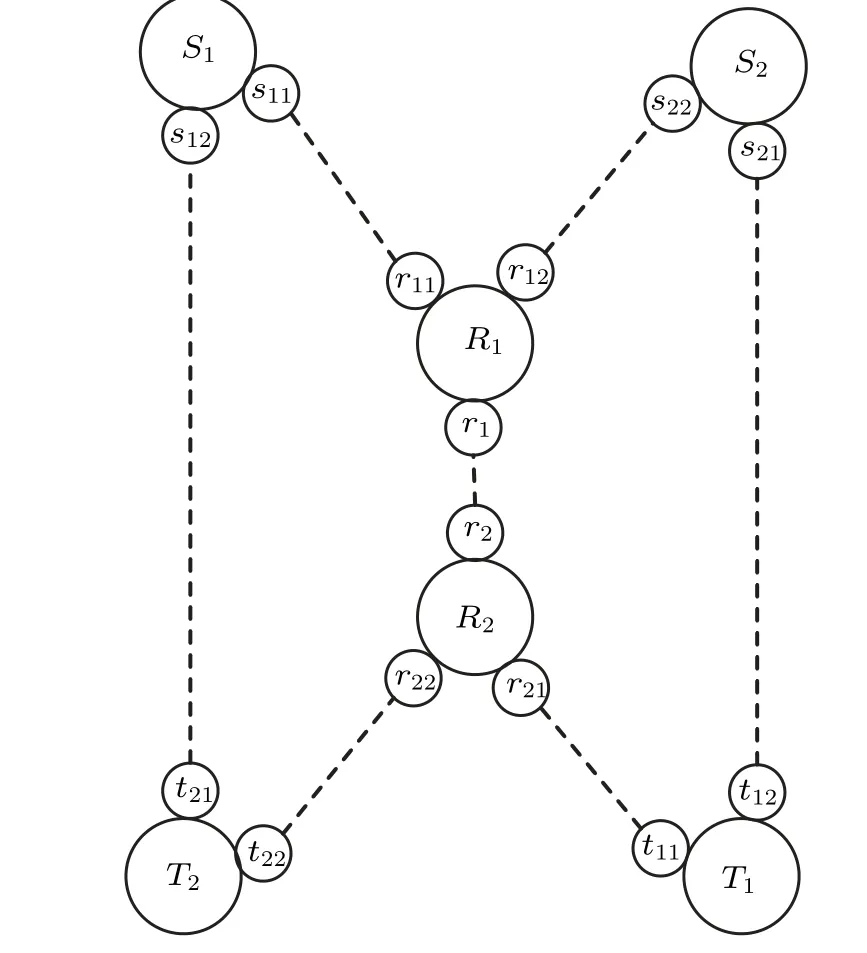
Fig.10. The butterfly network with entanglement.

Thirdly, quantum measurements and encoding process.The combined state of|ψi〉iand|Ψ+〉siitiiat each senderSi(i ∈(1,2))is

Each senderSiuses Bell basis{|Ψ+〉,|Ψ-〉,|Φ+〉,|Φ-〉}to measure particlesi,sii, which is a quantum non-demolition measurement. The measurement results of Bell basis are encoded into 2-bitXiaccording to Table 6.

Table 6. Bell measurements coding table.

After senderSiperforms Bell basis measurement,follow by sending particleito Victor. Victor uses the single particle basis{|m〉i,|n〉i}to measure particlei, and encodes the measurement result with 1-bitYias shown in Table 7, whereYi,jrepresents the encoding result of thej-the single particle basis measurement applied by Victor to the senderSi. After Victor performs the single particle basis measurement,senderSiwill get quantum stateU(Yi)|ψ〉siior quantum complementary stateU(Yi)|ψ⊥〉sii. According to theYireceived from Victor,senderSiapplies recovery operationU(Yi)to obtain|ψ〉siior|ψ⊥〉siiwith equal probability.

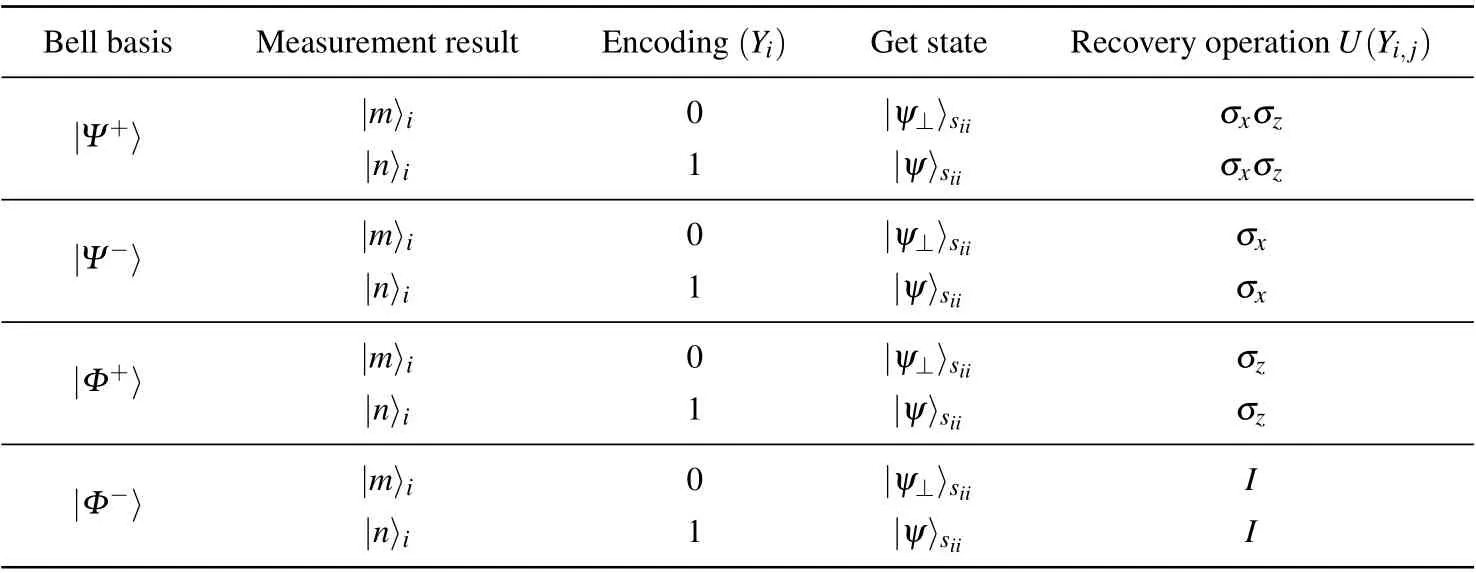
Table 7. Single particle basis coding table.

Finally, transmission and decoding process. SenderS1sendsX1to intermediate nodeR1and receiverT2via classic channelsC(S1,R1) andC(S1,T2), respectively. SenderS2sendsX2to intermediate nodeR1and receiverT1via classic channelsC(S2,R1)andC(S2,T1),respectively. An XOR operation is performed to getX1⊕X2atR1, andX1⊕X2is transmitted to next nodeR2. AtR2,X1⊕X2is copied and transmitted to receiversT1andT2via classic channelsC(R2,T1)andC(R2,T2), respectively. ReceiverT1performs the XOR operation(X1⊕X2)⊕X2to obtainX1,and applies unitary operationU(X1)-1to quantum stateU(X1)|ψ1〉t11to get quantum state|ψ1〉t11. ReceiverT2performs the XOR operation(X1⊕X2)⊕X1to obtainX2, and applies unitary operationU(X2)-1to quantum stateU(X2)|ψ2〉t22to get quantum state|ψ2〉t22. SenderS1sends quantum state|ψ1〉or quantum complement state|ψ1⊥〉to receiverT2through quantum channelQ(S1,T2). SenderS2sends quantum state|ψ2〉or quantum complement state|ψ2⊥〉to receiverR1through quantum channelQ(S2,T1).

Through the above four stages, quantum state|ψ1〉with probability 1 and quantum state|ψ2〉with probability 1/2 or quantum complement state|ψ2⊥〉with probability 1/2 can be obtained at receiverT1. Quantum state|ψ2〉with probability 1 and quantum state|ψ1〉with probability 1/2 or quantum complement state|ψ1⊥〉with probability 1/2 can be obtained at receiverT2.It should be noted that if the amplitudes of the transmitted quantum states|ψ1〉1and|ψ2〉2are real numbers,Victor will apply the special single particle basis{|m〉=α|0〉+β|1〉,|n〉=β|0〉-α|1〉}to perform quantum measurements, then each receiverT1,T2receives both quantum states|ψ1〉and|ψ2〉with probability 1. Thereby, quantum 2-pair multicast communication can be completed over the butterfly network.

3.2. Quantum kkk-pair multicast communication scheme

We extend quantum 2-pair multicast communication to extended butterfly network,and propose quantumk-pair multicast communication scheme over the extended butterfly network.

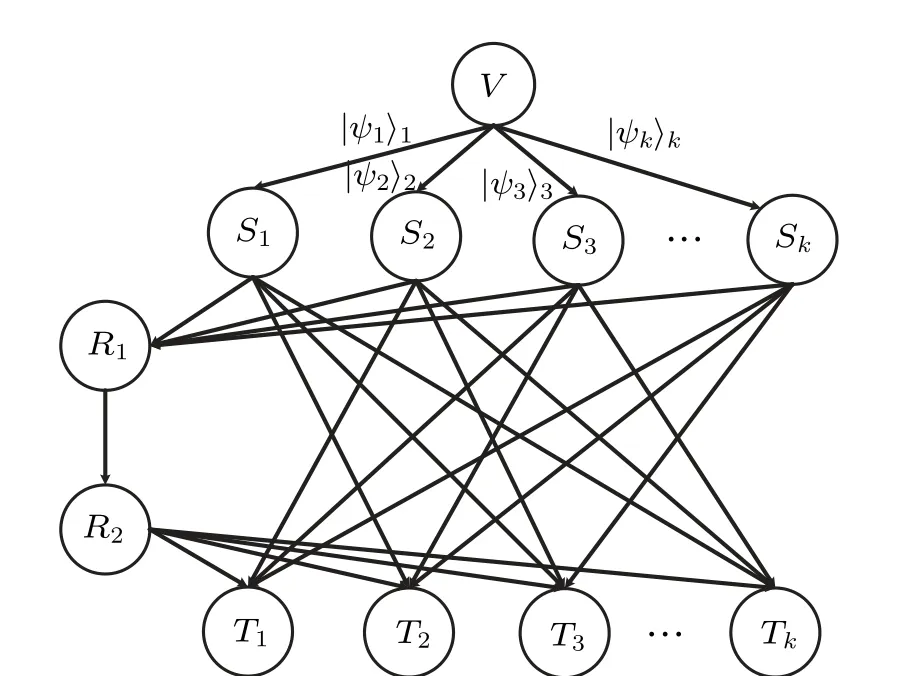
Fig.11. The extended butterfly network with preparer V.

Firstly, establishing entanglement relationship. The initial entanglement relationship over the extended butterfly network is shown in Fig. 12. By applying quantum operations introduced in Subsection 2.2,the entangled relationship is established between senderSiand receiverTi,i ∈{1,...,k}.

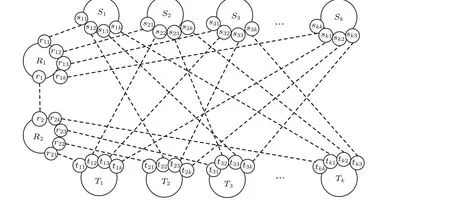
Fig.12. The extended butterfly network with entanglement.

The initial state of quantum system is

The quantum state|Γ1〉becomes

Each senderSiapplies Bell-basis to measure particle pairs (i,sii), (Auxi,1,Auxi,2),..., (Auxi,(k-2)×2-1,Auxi,(k-2)×2) successively, which is a quantum nondemolition measurement. After Bell-basis measurements,each receiverTiwill get one of the quantum states{|ψi〉tii,σz|ψi〉tii,σx|ψi〉tii,σzσx|ψi〉tii}. Each senderSisends particlesi,Auxi,1,...,Auxi,(k-2)×2-1to Victor. After receiving the single particles,Victor applies the special single particle basis{|m〉,|n〉}to measure the received particlesi,Auxi,1,...,Auxi,(k-2)×2-1. Here Victor will performk-1 single particle basis measurements. The basis{|m〉,|n〉}is

Victor encodes each measurement result with 1-bitYiaccording to Table 7,and transmits(k-1)bitsYito senderSi. Each senderSireceives (k-1) bitsYifrom Victor. When theYiis 0,quantum complement state is obtained at sender,otherwise quantum state is obtained. After Victor performs the special single particle measurement,The state of particlessii,Auxi,2,...,Auxi,(k-2)×2will be obtained at each senderSiin the following form:

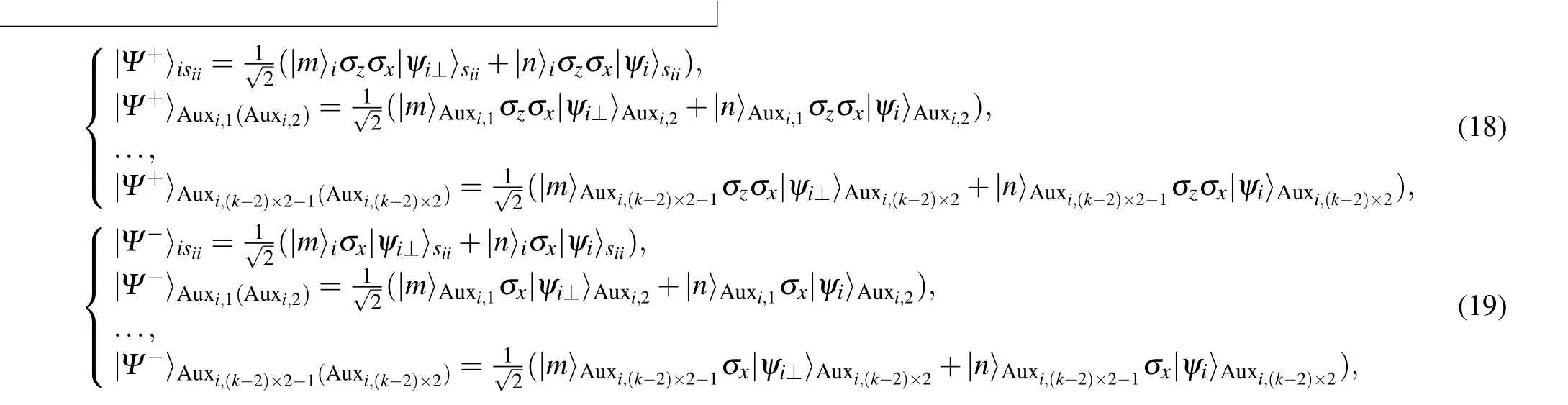
4. Conclusion

In this paper,we consider Bell states,auxiliary particles,and free classical channels as auxiliary resources to complete quantum multicast communication,which solve the bottleneck problem and improve the communication efficiency.Although auxiliary resources are consumed,quantum channels are used only once at most in our scheme. It should be noted that if the amplitudes of transmitted quantum states are real numbers,each receiver can receivekquantum states.

In our scheme,no matter how many times Bell basis measurements are applied, the receivers use only one of the following four unitary operations to recover the quantum state,that is,{I,σx,σz,σxσz}. Therefore, the capacity of classical channel is no more than 2 bits in our scheme. The maximum capacity of classical channels will not be increased with the increase of multicast numberk,which saves the utilization of classical channels to some extent.

At present, quantum multicast communication is in a booming stage. We are also the first attempt to study quantum multicast communication by adding auxiliary resources.Next,we will consider how to save resources to complete quantum multicast communication over the butterfly network,which is also the task we have been trying to solve.In the future,the establishment and application of quantum network[45-47]cannot be separated from quantum multicast communication.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 92046001, 61671087,61962009, and 61971021), the Fundamental Research Funds for the Central Universities (Grant Nos. 2019XD-A02 and 2020RC38), the Fund from Huawei Technologies Co. Ltd(Grant No. YBN2020085019), the Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data(Grant No. 2018BDKFJJ018), the Fundamental Research Funds for Beijing Municipal Commission of Education, the Scientific Research Launch Funds of North China University of Technology, and Beijing Urban Governance Research Base of North China University of Technology.