Huilai Zhang(張會(huì)來(lái)), Meiyu Peng(彭美瑜), Xun-Wei Xu(徐勛衛(wèi)), and Hui Jing(景輝)

Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education,

Department of Physics and Synergetic Innovation Center for Quantum Effects and Applications,Hunan Normal University,Changsha 410081,China

Keywords: anti-parity-time symmetry,optical gyroscope,exceptional point,Kerr nonlinearity

1. Introduction

Exceptional points (EPs)[1]are non-Hermitian spectral degeneracies,where both the eigenvalues and the corresponding eigenvectors of a system simultaneously coalesce. Nontrivial phenomena related to EPs have been of great interest,particularly in connection with parity-time(PT)[2-8]and anti-PT(APT) symmetries.[9,10]PT-symmetric systems have balanced loss and gain, and can exhibit EP with entirely real eigenvalues. Novel applications ofPTsystems such asPTsymmetric optomechanics,[11-14]topological photonics,[15,16]PTmetamaterials,[17,18]to name only a few, have been revealed. On the contrary,APTsymmetry[19]does not need gain [see Fig. 1(a)] but can still exhibit EP with entirely imaginary eigenvalues in the symmetric phase,[9]which has been extensively explored both in experiments[10,20-36]and in theories.[37-69]This striking difference provides us a variety of novel opportunities to exploreAPTeffects in atomic systems,[10,20]photonic or magnonic devices,[21-25]and thermal structures.[26,27]These systems are known to exhibit nontrivial phenomena such as chiral mode switching,[22]energy-difference conserving dynamics,[23,28]and constant refraction.[37]In particular, EP systems, including those withPTandAPTsymmetries,can open up a new route to make ultrasensitive sensors since they can display a strong response to perturbations near EPs.[70,71]

As highly sensitive rotation sensors,gyroscopes[72-74]are widely used in e.g. unmanned and autonomous vehicles and global navigation systems. The concept of EP sensing applied to ultrasensitive rotation measurement was first proposed in aPTsystem.[75]After that,several EP-based gyroscopes have been proposed usingPTorAPTsymmetry,[48,76-78]loss regulation,[79,80]and dissipative coupling.[81-83]Compared withPTgyroscope,APTgyroscope does not need gain,thus can be kept at EP more accurately.Moreover,APTgyroscope can exhibit a completely real frequency splitting which can be directly measured at the output power spectrum,[48]whilePTgyroscope usually exhibits complex frequency splitting.In addition, in two recent experiments, EP-based quasi-APT[84]and passive-PT[85]gyroscopes were demonstrated with a microresonator and a macroscopic triangular cavity,respectively.However,these studies mainly focused on the linear case. The effect of nonlinearity on EP gyroscope remains largely unclear,despite a few discussions along this line.[82,84,85]Given that the superior performance of linear EP gyroscope has been confirmed in the experiments,[84,85]it is thus necessary to go a step further to explore the role of nonlinearity inAPTgyroscope.

In a recent experiment,[86]a spinning resonator was used for realizing nonreciprocal light transmission with 99.6%rectification. Such spinning resonators[87-95]have also been applied to single-photon control,[87,88]single nanoparticles sensing,[89]and backscattering immune optomechanical entanglement generation,[90]to name a few. We also find that[40]the opposite Sagnac-Fizeau shifts in counter-propagating modes of the resonator can be utilized for creating anAPTsymmetric system. Moreover,this system is linear and can be readily extended to a system with nonlinear materials.

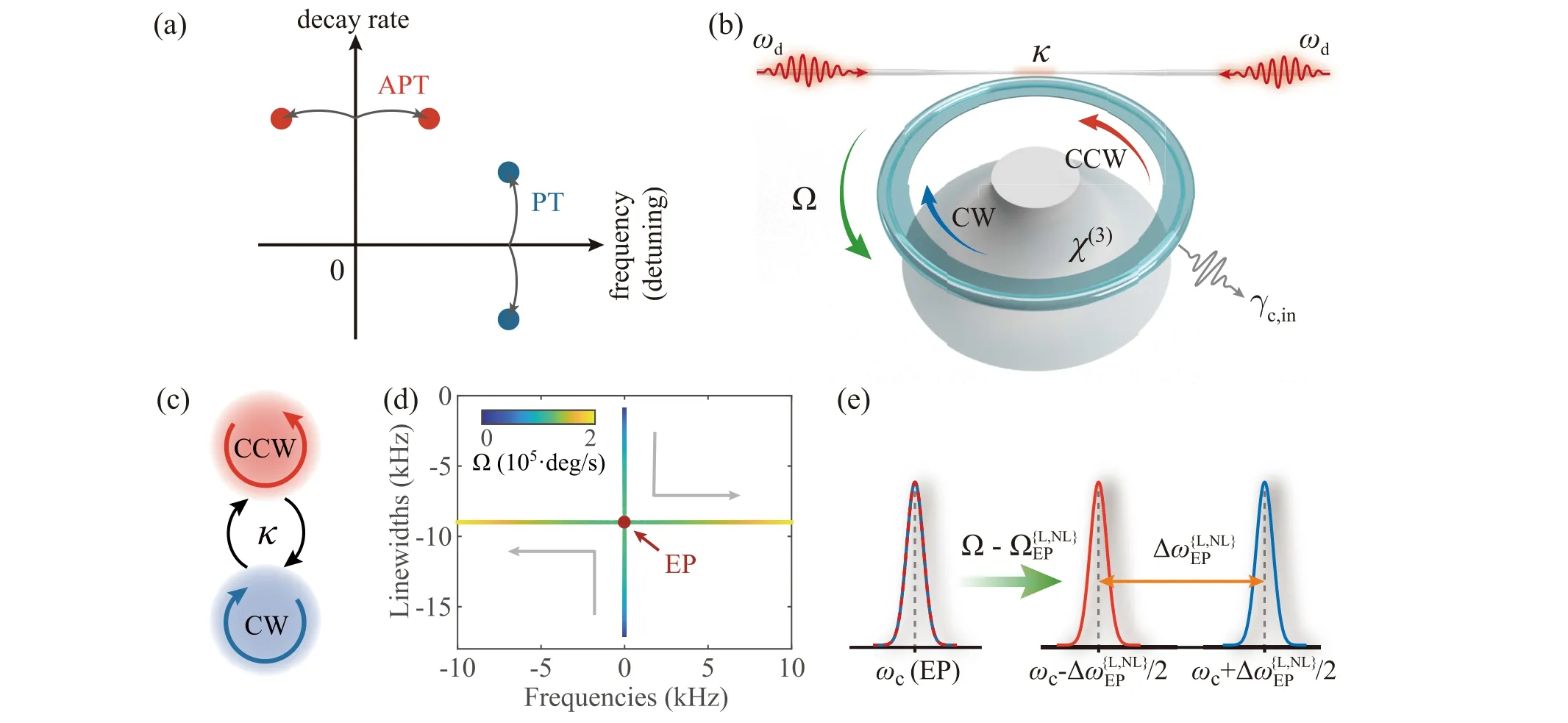
Fig.1. Anti-parity-time(APT)-symmetric gyroscope. (a)Comparison between PT and APT symmetries. The dark red dots indicate the APT coupled optical modes with the same passive loss and opposite detunings. The dark blue dots indicate the PT coupled optical modes with the same frequency (detuning) and balanced gain and loss. (b) Schematic of a nonlinear APT gyroscope based on an optical spinning resonator.(c) Schematic of dissipatively coupled counterpropagating modes. (d) Linear eigenfrequencies versus rotation speed Ω in the complex plane.(e)Mechanism of APT gyroscope.

To explore the role of nonlinearity inAPTgyroscope,in this work, we propose a nonlinearAPT-symmetric optical gyroscope based on a spinning resonator with Kerr nonlinearity of the materials. To have a better comparison,we examine theAPTgyroscope without nonlinearity first,and show that the sensitivity of frequency splitting can be magnified 4.9×103times that of a conventional device without EPs. Then, in the presence of Kerr nonlinearity[96-98]of materials, we find that the sensitivity can be further enhanced inAPT-symmetry-broken (APTB) regime, which isAPTsymmetric (APTS) in the linear device. The nonlinearityinduced phase transition is reminiscent of the similar effects inPTsystems.[4,99]Remarkably, the detection threshold of theAPTgyroscope can be significantly lowered, i.e., much weaker rotations which are well beyond the ability of a linear device can now be detected with the nonlinear one. The parameters used for numerical simulations are experimentally feasible.[84,86,100-102]Our work shows the powerful ability ofAPTgyroscopes in practice to achieve ultrasensitive rotation measurement.

2. APT-symmetric gyroscope

2.1. Model and Hamiltonian

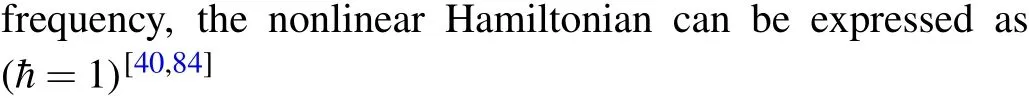
where the dispersion term dn/dλcharacterizing the relativistic origin of the Sagnac effect is relatively small (～1%) in typical materials of microresonator. Then the Hamiltonian of the spinning system can be obtained as We use the following parameters in numerical simulations:λ=1550nm,Q ≈2×1010,γex=γc,in,κ=8kHz,n=1.44,R= 50μm, as in relevant experiments.[84,86,100]The coefficient of Kerr nonlinearitygis chosen to be 0.17Hz according to the experimentally feasible parameters:[101,102]nNL=3.2×10-16cm2/W andVeff=102μm3.

2.2. Linear APT gyroscope

The evolution of the eigenfrequencies in the complex plane is plotted as a function of the rotation speed Ω in Fig. 1(d).As depicted in Fig.1(d),the eigenfrequency splitting is purely imaginary inAPTS regime before EP. WhenΔsag=κ, i.e.,ΩLEP≈1.2×105deg/s,this system is at EP where the real and imaginary parts of the eigenfrequencies simultaneously coalesce. By further increasing the rotation speed,a real splitting of eigenfrequencies can be observed inAPTB regime. Thus,this spinningAPTresonator can function as a gyroscope for rotation measurement around EP by breakingAPTsymmetry,as illustrated in Fig.1(e).

In Fig.2(a),we plot the real parts of the eigenfrequencies Re[ωL±]versus rotation speed Ω. A conventional gyroscope is shown for comparison,in which the real parts of the eigenfrequencies are proportional to the rotation speed,see the dashed curves in Fig. 2(a). ForAPTgyroscope, the eigenfrequencies are locked inAPTS regime before EP,creating a measuring dead band for rotations.[83,84]While in theAPTB regime(shaded regime in Fig.2),the rotation speed over ΩLEPleads to a splitting between the unlocked eigenfrequencies,which is

Figure 2(b) provides a comparison betweenAPTand conventional gyroscopes, from which the frequency splitting of theAPTgyroscope can be observed in theAPTB regime.For the conventional gyroscope,a frequency splitting emerges once a rotation is applied to the system.

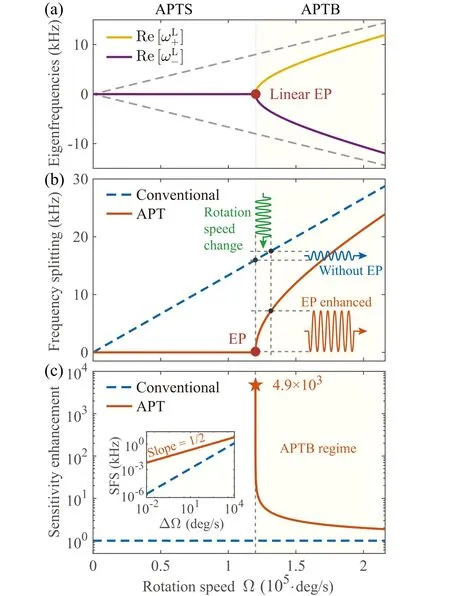
Fig.2. Linear APT gyroscope. (a)Real parts of eigenfrequencies of conventional (dashed curves) and APT (solid curves) gyroscopes versus the rotation speed Ω. (b) Frequency splitting versus the rotation speed Ω in the conventional (blue dashed curve) and APT (orange solid curve) gyroscopes. (c) Sensitivity enhancement versus the rotation speed Ω (orange solid curve). The blue dashed curve is corresponding to the conventional gyroscope. The inset shows the shifted frequency splitting(SFS)versus the change of rotation speed ΔΩ=Ω-ΩLEP.

2.3. Nonlinear APT gyroscope

We have confirmed that the frequency splitting can be enhanced in the linearAPTgyroscope above. Now we explore the role of nonlinearity inAPTgyroscope. According to Eq.(3),the equations of motion can be derived as

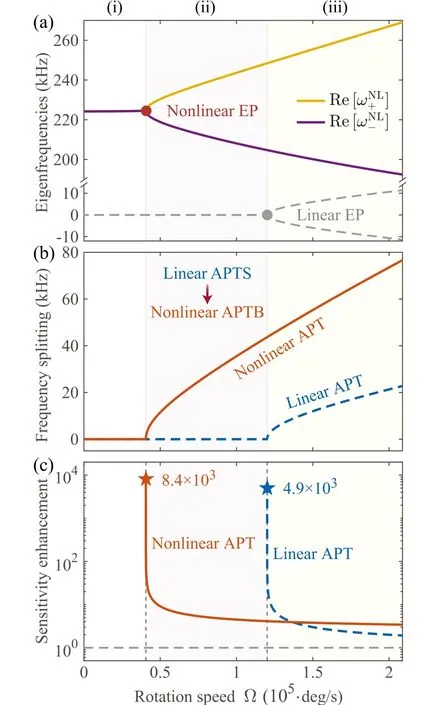
Fig. 3. Nonlinear APT gyroscope. (a) Real parts of eigenfrequencies of the nonlinear (solid curves) and linear (dashed curves) APT gyroscopes versus the rotation speed Ω. (b) Frequency splittings of the nonlinear (orange solid curve) and linear (blue dashed curve) APT gyroscopes versus Ω. (c) The nonlinear (orange solid curve) and linear (blue dashed curve)sensitivity enhancements versus Ω. g is chosen to be 0.17Hz according to the experimentally feasible parameters:[101,102] nNL =3.2×10-16 cm2/W and Veff=102μm3. The pump power is P=25nW.

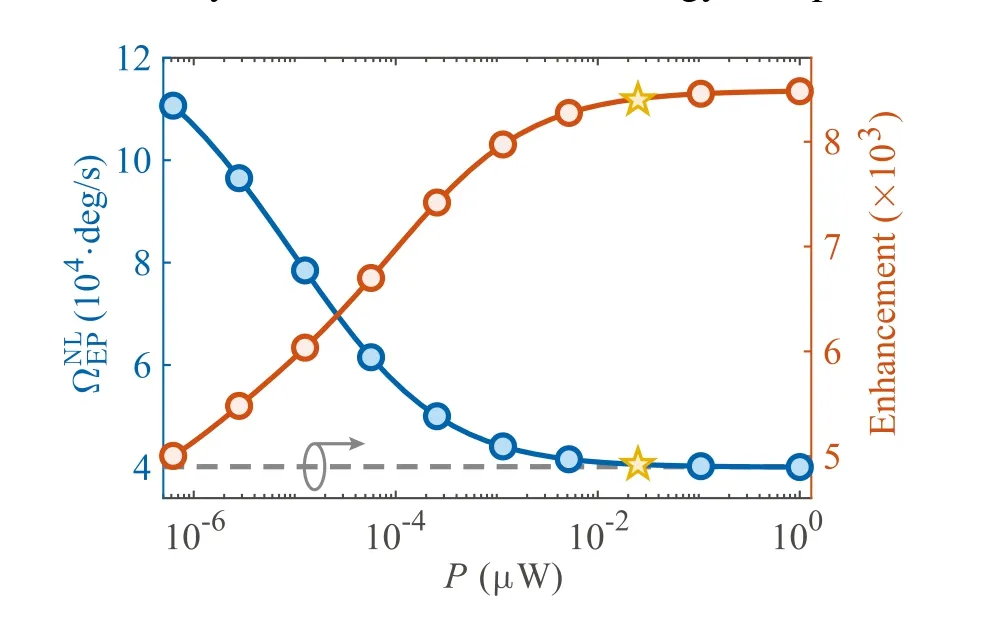
Fig. 4. Rotation speed corresponding to nonlinear EP and sensitivity enhancement in respect to a detectable change of rotation speed of 0.01deg/s from versus the pump power P. The dashed curve indicates the sensitivity enhancement of linear APT gyroscope.The parameters used are the same as those in Fig.3.

3. Conclusion

We have proposed a nonlinearAPToptical gyroscope and compared its performance with the linear device. We find triple advantages for introducing Kerr nonlinearity into theAPTsystem: (i) the sensitivity can be enhanced with weak and experimentally accessible Kerr nonlinearity;(ii)the measurable regime of weak rotations can be efficiently extended by breaking theAPTsymmetry due to the Kerr nonlinearity;(iii)the EP position of the gyroscope can be continuously tuned in a wide range by changing the pump power,providing a feasible way to enhance the performance of the gyroscopeon-situ.

Our work confirms thatAPTdevices can serve as a powerful tool for highly sensitive rotation measurement and can be extended to study the role of nonlinearity in higher-order EP sensors. Moreover,our proposal can be applied to otherAPTsystems with various types of nonlinearity such as secondorder nonlinearity,[106]optomechanical interactions,[107]and hybridized atom-cavity interactions.[108]

Note added After submission of this paper, we noticed a new experiment on nonlinear enhanced microresonator gyroscope,[109]which demonstrated an optical gyroscope with a responsivity enhanced by a factor of around 104using the critical point of a spontaneous symmetry-breaking transition between counterpropagating light.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos. 11935006, 11774086, and 12064010), Science and Technology Innovation Program of Hunan Province, China (Grant No. 2020RC4047), Natural Science Foundation of Hunan Province of China (Grant No.2021JJ20036),and Natural Science Foundation of Jiangxi Province of China(Grant No.20192ACB21002).