,

(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

Abstract: Fixed point theory has become an important part of nonlinear functional analysis and a rapidly developing subject, which has attracted much attention in recent years. The research results of this problem have been successfully applied in the fields of partial differential equations, cybernetics, economic balance theory and game theory, and are closely related to many branches of modern mathematics. Firstly, we establish a new type of (ψ,φ)-weak contractive condition in the b-metric-like spaces and construct a sequence {yn} in X. Then, by using the conditions of ψ,φ and reduction to absurdity, we prove that we prove that {yn} is a Cauchy sequence in X. Finally, according to the completeness of X and our new contractive mappings, we conclude that f and g have a unique coincidence point in X. Moreover, f and g have a unique common fixed point provided that f and g are weakly compatible. Meanwhile, an example is provided to illustrate the effectiveness of the result.

Key words: common fixed point; (ψ,φ)-weakly contractive mappings; b-metric-like spaces; weakly compatible

0 Introduction

Banach contraction mapping principle[1]is one of the most essential aspects of fixed point theory as a source of the existence and uniqueness of solutions of many problems in all kinds of branches inside and outside mathematics. This celebrated principle has been generalized by several authors. In 1993, Czerwik[2]introduced the concept of theb-metric space as a generalization of metric space, and he also proved contraction mapping principle inb-metric space. From that time on, some authors have introduced some generalizations ofb-metric space. For example, Hussain and Shah in[3]introduced the notion of a coneb-metric space, which means that it is a generalization ofb-metric spaces and cone metric spaces, they considered topological properties of coneb-metric spaces and obtained some results on KKM mappings in the setting of coneb-metric spaces. Furthermore, Zoto et al[4]got some fixed point results concerning (s,p,α)-quasi-contractions and (s,p)-weak contractions in theb-metric-like spaces. Another offshoot of generalizations of Banach contraction mapping principle is based on exploring some new contraction-type mappings. In 1997, Gohberg et al[5]introduced the concept of weak contraction. They also proved that eachφ-weak contraction on a Hilbert space had a unique fixed point. Since then, Rhoades[6]showed that the results are also valid for any Banach space. Rhoades has done initial work that stimulated many researchers to prove fixed and common fixed point theorems for a fewφ-and (ψ,φ)-weakly contractive mappings, see[7-9]. In particular, Aghajani et al[10]presented several common fixed point results of generalized weak contractive mappings in partially orderedb-metric spaces.

In this paper, we aim to study common fixed point result involving generalized (ψ,φ)-weakly contractive conditions inb-metric-like space. In addition, we provide an example to support our result.

1 Preliminaries

The following definitions will be needed in the sequel.

Definition1[4]LetXbe a nonempty set ands≥1 be a given real number. A mappingd:X×X→[0,∞) is said to be ab-metric-like if and only if, for allx,y,z∈X, the following conditions are satisfied:

1)d(x,y)=0 impliesx=y;

2)d(x,y)=d(y,x);

3)d(x,y)≤s(d(x,z)+d(y,z)).

In general, (X,d) is called ab-metric-like space with parameters≥1.

Example1 LetX=+, and let the mappingd:X×X→+be defined byd(x,y)=(x+y)2for allx,y∈X. Then (X,d) is ab-metric-like space with parameters≥2.

Proof. We can infer from the convexity of the functionf(x)=x2(x>0) that (a+b)2≤2(a2+b2) holds. Then forx,y,z∈X, we have

d(x,y)=(x+y)2≤(x+z+y+z)2≤2[(x+z)2+(y+z)2]=2d(x,z)+2d(z,y)

In this case, (X,d) is ab-metric-like with parameters=2.

Definition2[4]Let (X,d) be ab-metric space with parameters≥1. A sequence {xn} inX, then

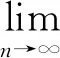
2) {xn} is a Cauchy sequence if and only ifd(xn,xm) exists and is finite;

3) (X,d) is called complete if for each Cauchy sequence, there exists anx∈Xsuch that

Definition3[4]Letfandgbe two self-mappings on a nonempty setX. Ifw=fx=gx, for somex∈X, thenxis said to be the coincidence point offandg, wherewis called the point of coincidence offandg. LetC(f,g) denote the set of all coincidence points offandg.

Definition4[11]Letfandgbe two self-mappings defined on a nonempty setX. Thenfandgis said to be weakly compatible if they commute at every coincidence point, that is,fx=gx?fgx=gfxfor everyx∈C(f,g).

The following lemmas are essential for our main results.

Lemma1[4]Let (X,d) be ab-metric-like space with parameters≥1. We assume that {xn} and {yn} converges toxandy, respectively. Then we have

Moreover for eachz∈X,ifd(x,x)=0, then

Lemma2[12]Let (X,d) be ab-metric-like space with parameters≥1. Then

1) Ifd(x,y)=0, thend(x,x)=d(y,y)=0;

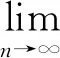
3) Ifx≠y, thend(x,y)>0.

2 Main Results

Now we state our main results as follows:

Theorem1 Let (X,d) be a completeb-metric-like space withs≥1 and letf,g:X→Xbe given self-mappings onXsatisfyingf(X)?g(X) andg(X) is a closed subset ofX. If there exist functionsψandφsuch thatψ,φ:[0,∞)→[0,∞) are increasing and continuous functions withφ(t)=0?t=0, for allx,y∈X,

ψ(s2[d(fx,fy)]2)≤ψ(N(x,y))-φ(L(x,y))

(1)

where

thenfandghave a unique point of coincidence inX. Moreover,fandghave a unique common fixed point provided thatfandgare weakly compatible.

Proof. Letx0∈X. It follows fromf(X)?g(X), there existsx1∈Xsuch thatfx0=gx1. Continuing the process, we obtain two sequences {xn} and {yn} inXbyyn=fxn=gxn+1for alln∈N. Ifyn=yn+1for somen∈N, then we haveyn=yn+1=fxn+1=gxn+1which implies thatfandghave a point of coincidence. Suppose thatyn≠yn+1(by Lemma 2, we know thatd(yn,yn+1)>0) for alln∈N. Applying (1) withx=xnandy=xn+1, we obtain

ψ(s2[d(yn,yn+1)]2)=ψ(s2[d(fxn,fxn+1)]2)≤ψ(N(xn,xn+1))-φ(L(xn,xn+1))

(2)

where

and

If we assume that, for somen∈N,

d(yn,yn+1)≥d(yn,yn-1)>0

then, from equations (3) and (4), we are aware of

Taking advantage of (2), and the above results, we get

which implies toφ([d(yn,yn+1)]2)=0, that is,yn=yn+1, a contradiction. It follows that {d(yn,yn+1)} is a non-increasing sequence. Consequently, there existsr≥0 such that

Now we prover=0. If we assume thatr>0, then taking the limit asn→+∞ in (2), using the continuity ofψandφ, one can obtainψ(r2)≤ψ(r2)-φ(r2), which gives a contradiction. Hence,

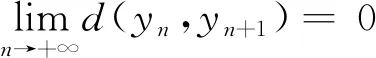
(6)

In view of the triangle inequality, one can assert that

Lettingk→∞ and using (6), we have

Using the same method, we deduce that

From (7), we obtain

Using (8) and (9), we have

By the similar method, we infer

So there is

It follows from the definition ofN(x,y) that

which yields

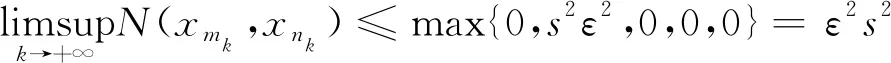
(10)

Similarly, we have

So we conclude that

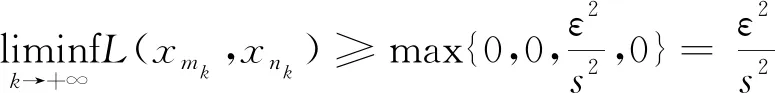
(11)

Applying (1) withx=xmkandy=xnk, we get

ψ([d(ymk,ynk)]2)≤ψ(s2[d(ymk,ynk)]2)≤ψ(N(xmk,xnk))-φ(L(xmk,xnk))

By virtue of (10), we have

which implies that

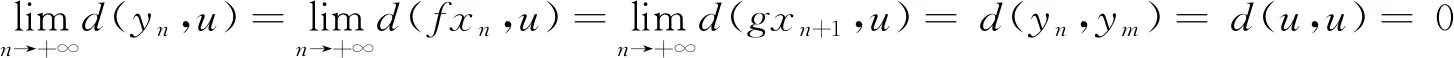
(12)

And we haveu∈g(X) sinceg(X) is closed. Obviously, one can choose az∈Xsuch thatu=gz, so (12) can be replaced by

Iffz≠gz, applying contractive condition (1) withx=xnk, andy=z, we have

ψ(s2[d(ynk,fz)]2)=ψ(s2[d(fxnk,fz)]2)≤ψ(N(xnk,z))-φ(L(xnk,z))

(13)

where

and

Considering the above equations, we obtain

and

Taking the upper limit ask→∞ in (13), we have

which implies that

d(fz,gz)=0

That is,fz=gz. Therefore,u=fz=gzis a point of coincidence forfandg. We easily obtain that the point of coincidence is unique. And by the weak compatible property offandgit can be shown thatzis a unique common fixed point. This completes the proof.

In order to verify our main results, we furnish an illustrative example which demonstrates the validity of the hypotheses.

Example2 LetX=[0,1] be endowed with theb-metric-liked(x,y)=(x+y)2for allx,y∈Xands=2. Define mappingsf,g:X→Xby

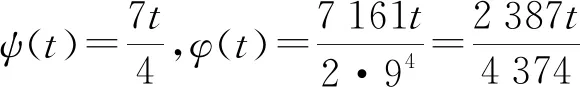
Based on the points discussed above, we may reasonably draw the conclusion that

Therefore, the contractive condition of Theorem 1 is satisfied. And 0 is the unique common fixed point offandg.

3 Conclusions

In this paper, we introduced new generalized (ψ,φ)-weakly contractive mappings and obtained a common fixed point theorem in the framework ofb-metric-like space. Further,we provided an example that elaborated the usability of our result.