洪 勇,吳春陽,陳 強

(1. 廣東白云學(xué)院 數(shù)學(xué)教研室,廣州 510450；2. 廣東第二師范學(xué)院 計算機(jī)科學(xué)系,廣州 510303)

1 引言與預(yù)備知識

設(shè)r>1,α∈,定義函數(shù)空間為

為Hilbert型積分不等式. 若λ1λ2>0,K(x,y)=G(xλ1yλ2)≥0,引入搭配參數(shù)a,b,根據(jù)H?lder不等式,利用權(quán)系數(shù)方法,可得如下形式的該類非齊次核的Hilbert型積分不等式：

(1)

一般地,該不等式的常數(shù)因子W(a,b,p,q,λ1,λ2)并不是最佳的,只有在一些特定條件下,其常數(shù)因子才是最佳的. 目前,研究者們基本上都憑經(jīng)驗選擇適當(dāng)?shù)拇钆鋮?shù)a,b,得到具有最佳常數(shù)因子的Hilbert型積分不等式[1-6]. 本文通過對文獻(xiàn)[7-12]進(jìn)行分析,針對非齊次核K(x,y)=G(xλ1yλ2)的情形,試圖找出某種規(guī)律,以解決最佳搭配參數(shù)a,b的選擇問題.

若搭配參數(shù)a,b能使W(a,b,p,q,λ1,λ2)是式(1)的最佳常數(shù)因子,則稱a,b為適配參數(shù)或適配數(shù). 由于式(1)與Hilbert型積分算子：

(2)

關(guān)系密切,討論適配數(shù)等價于討論算子T的范數(shù),因此尋求適配數(shù)的充要條件具有重要的理論意義.

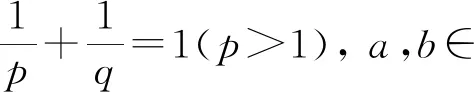
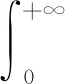
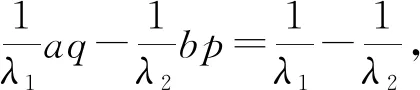
同理可證ω2(a,q,y)=y(λ2/λ1)(aq-1)W2(a,q).

2 適配數(shù)的充分必要條件

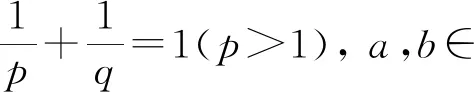
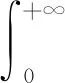
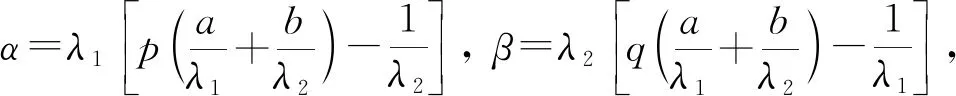
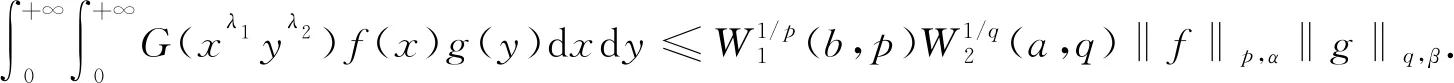
(3)

(4)

其中W0=|λ1|W2(a,q)=|λ2|W1(b,p).

證明：1) 選擇a,b為搭配參數(shù). 利用權(quán)系數(shù)方法,根據(jù)引理1,有

故式(3)成立.

于是式(3)可化為式(4).

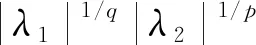
取充分小的ε>0及足夠大的自然數(shù)n,令

經(jīng)計算可得

于是可得

則

由計算可得

于是,可知式(3)等價于

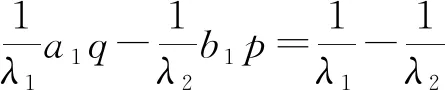
(5)

于是可得

(6)

根據(jù)H?lder不等式,有

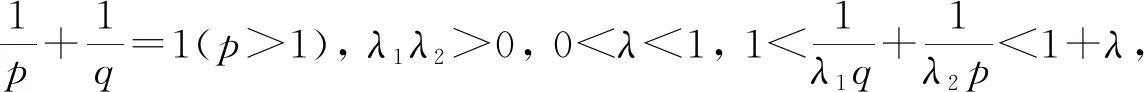
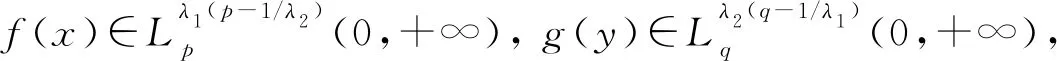
是最佳的.

證明：選取搭配參數(shù)

由計算可知

又因為

且

因此根據(jù)定理1知推論1成立.

3 應(yīng) 用

設(shè)積分算子T定義如式(2). 根據(jù)Hilbert型不等式的基本理論,式(3)等價于不等式

于是由定理1可得如下結(jié)果：

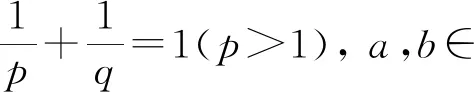
a0pq-1=p(1-λ1)-1=α,b0pq-1=q(1-λ2)-1=β,

且

故a0,b0是適配參數(shù).

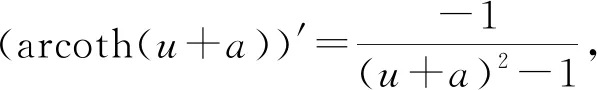
根據(jù)定理2知推論2成立.