郭世樂

（福建技術(shù)師范學(xué)院電子與信息工程學(xué)院,福建福清 350300 ）

1 預(yù)備知識

本文所有環(huán)均指含有單位元的結(jié)合環(huán).非交換環(huán)在環(huán)論中有著重要地位,得到廣泛的重視和研究.1973年,Shin[1]提出了半交換環(huán)的概念并研究了半交換環(huán)的一些性質(zhì).此后, 人們對半交換及其推廣進行了廣泛的研究[2-20].Chen[2]提出了nil-半交換環(huán)的概念,郭世樂[3]提出了qnil-半交換環(huán)的概念,謝雪[4]利用環(huán)的Jacobson根,提出了J-半交換環(huán)的概念,討論了J-半交換環(huán)的性質(zhì)與擴張.

定義1[1]一個環(huán)R稱為半交換環(huán),如果對任意a, b∈R, 當ab=0時有aRb=0.

定義2[3]一個環(huán)R稱為J-半交換環(huán),如果對任意a, b∈R, 當ab=0時有aRb? J(R),其中 J(R)是R的Jacobson根.

2 J-半交換環(huán)的基本性質(zhì)

顯然,半交換環(huán)必是J-半交換環(huán).下面例子說明反之不成立.

例[3]令

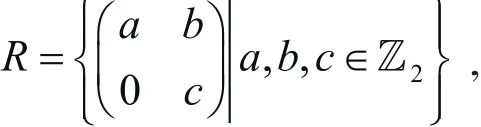
其中?2是整數(shù)環(huán)?模2剩余類環(huán), 則R是J-半交換環(huán)但卻不是半交換環(huán). 因為存在R中元素

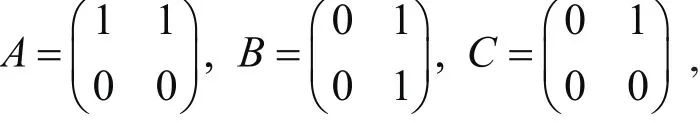
滿足 AB=0, 而 ACB≠0, 所以R不是半交換環(huán).另一方面,可以斷言R是J-半交換環(huán),事實上,易見

所以R是J-半交換環(huán).

定理1設(shè) I是環(huán)R的理想, 且I?J(R). 若

R/I是J-半交換環(huán), 則R也是J-半交換環(huán).

證明 若R/I是J-半交換環(huán). 任取a,b ∈ R滿足ab=0, 則ab=0,可得a(R/I)b ? J(R/I ).對于R中任意元素r, 有arb ∈ J(R/I ).則對任意的x ∈ R,1 - x (a rb) ∈ U(R/I).存在s ∈ R使得(1 - x (a rb))s =1,因此1 - ( 1 - x (a rb))s ∈ I ? J(R).故1 - ( 1 - ( 1 - x (a rb))s) ∈ U(R),易得,1 - x (a rb ) ∈U∈U(R). 因此arb ∈ J(R), 從而R是J-半交換環(huán).

推論 若R/J(R)是J-半交換環(huán),則環(huán)R也是J-半交換環(huán).

3 J-半交換環(huán)進一步探討

引理1[5]設(shè)H(R) 是環(huán)R上的 Hurwitz 冪級數(shù)環(huán), 則U(H(R))={f (x) =a0+a1x+a2x2+…|a0∈U(R)}.

引理2[5]設(shè)H(R) 是環(huán)R上的 Hurwitz 冪級數(shù)環(huán), 則J(H(R))={f (x) =a0+a1x+a2x2+…|a0∈J(R)}.

定理2環(huán)R上的 Hurwitz 冪級數(shù)環(huán)H(R)是J-半交換環(huán)當且僅當R是J-半交換環(huán).

證 明若H(R)是J-半交換環(huán).任取a,b ∈ R滿足ab=0,對于任意的r ∈ R,arb ∈ J(H(R)).對于任意的y∈ R ? H(R),可得1 - y(a rb ) ∈ U(H(R)),故.因此R是J-半交換環(huán).

若R是 J-半交換環(huán). 則有環(huán)同態(tài)

對于環(huán)R以及環(huán)R的自同態(tài)α： R → R,R[[x;α]]中元素的形式和加法運算與形式冪級數(shù)環(huán)R[[x]]一致, 對于任意的r ∈ R,R[[x;α]]的乘法運算定義為xr=α(r)x.

引理3[5]設(shè)R[[x;α]]是環(huán)R上的斜冪級數(shù)環(huán),則

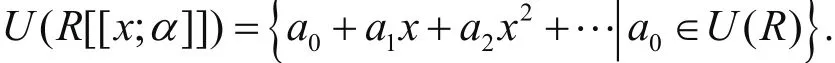
引理4[5]設(shè)R[[x;α]]是環(huán)R上的斜冪級數(shù)環(huán),則

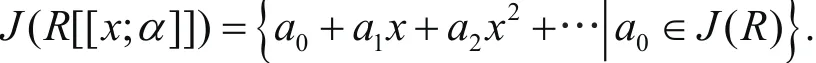
顯然, RG是一個環(huán),稱為群環(huán).

定理4設(shè)R是一個環(huán),G是一個 p-群, 且CharR=ps(s ≥≥1),其中p是素數(shù).則RG是 J-半交換環(huán)當且僅當R是J-半交換環(huán).

據(jù)定理1,RG是J-半交換環(huán).