章 溢, 熊 佳, 溫利民, 吳賢毅, 周 憲

(1.江西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,江西南昌330022;2.江西財(cái)經(jīng)大學(xué)統(tǒng)計(jì)學(xué)院,江西南昌330013;3.華東師范大學(xué)統(tǒng)計(jì)學(xué)院,上海200062;4.麥考瑞大學(xué)統(tǒng)計(jì)與精算學(xué)系,澳大利亞悉尼2109)

§1 引 言

在非壽險(xiǎn)精算中,常用非負(fù)隨機(jī)變量X表示風(fēng)險(xiǎn)的損失.一般地,風(fēng)險(xiǎn)X的分布依賴某個(gè)風(fēng)險(xiǎn)參數(shù)θ,記f(x;θ)表示風(fēng)險(xiǎn)X的密度函數(shù)或概率分布律.由于保單風(fēng)險(xiǎn)的非齊次性,所有θ的取值形成某個(gè)概率分布π(θ).在Bayes統(tǒng)計(jì)中,π(θ)被稱為先驗(yàn)分布,在精算學(xué)中又被稱為結(jié)構(gòu)函數(shù).假設(shè)對(duì)風(fēng)險(xiǎn)X已經(jīng)有若干年的索賠記錄X1,···,Xn,可看成θ給定條件下的獨(dú)立同分布的隨機(jī)樣本.本文的目的是通過結(jié)合樣本信息和先驗(yàn)分布信息對(duì)風(fēng)險(xiǎn)X或其分布f(x;θ)進(jìn)行估計(jì)或統(tǒng)計(jì)推斷.顯然,對(duì)f(x;θ)的統(tǒng)計(jì)推斷落入了Bayes框架.

在非壽險(xiǎn)精算中,信度理論是解決非齊次保單定價(jià)的一種重要方法,在保費(fèi)厘定,責(zé)任準(zhǔn)備金評(píng)估等方面都有廣泛的運(yùn)用[1-6].假設(shè)隨機(jī)變量X1,···,Xn與X是在風(fēng)險(xiǎn)參數(shù)θ給定條件下相互獨(dú)立同分布的隨機(jī)變量,其共同的密度函數(shù)為f(x;θ).為了預(yù)測未來的損失X或估計(jì)條件均值μ(θ)=E(X|θ),Bühlmann[1]建議將估計(jì)限定在樣本的線性損失函數(shù)下,求解下面的最小化期望平方損失問題

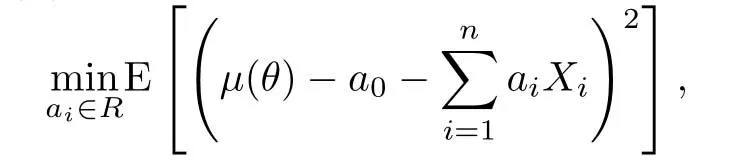
得到了條件均值μ(θ)的信度估計(jì)表達(dá)為下面的加權(quán)平均形式:

其中μ0=E[μ(θ)]為保單組合的聚合保費(fèi),而權(quán)重

被稱為信度因子.這里φ=E[Var(X|θ)],ρ=Var(μ(θ))

在數(shù)理統(tǒng)計(jì)中,核密度估計(jì)是密度函數(shù)的一種最為流行的非參數(shù)估計(jì)方法.核估計(jì)方法首次由Rosenblatt[11]提出,在生物統(tǒng)計(jì),醫(yī)學(xué)統(tǒng)計(jì),教育統(tǒng)計(jì)等領(lǐng)域有廣泛的運(yùn)用[12-15].

借助核估計(jì)思想,本文將建立損失額分布的Bayes模型,將條件密度的估計(jì)限定在核函數(shù)的線性結(jié)構(gòu)中,通過求解最小化期望積分損失函數(shù),得到密度函數(shù)的信度估計(jì).進(jìn)而通過代入的方法得到具有安全負(fù)荷的保費(fèi)原理中風(fēng)險(xiǎn)保費(fèi)的信度估計(jì).后面的內(nèi)容安排如下.§2介紹核密度估計(jì)并建立損失密度函數(shù)的Bayes模型.§3討論密度函數(shù)的核估計(jì)及其統(tǒng)計(jì)性質(zhì).§4在一些保費(fèi)原理中,獲得風(fēng)險(xiǎn)保費(fèi)的信度估計(jì),并與已有的信度估計(jì)進(jìn)行比較.

§2 模型的準(zhǔn)備與設(shè)定

記F(x)=P(X≤x)為風(fēng)險(xiǎn)X的分布函數(shù),相應(yīng)的密度函數(shù)為f(x).假設(shè)X1,···,Xn為該總體的n個(gè)獨(dú)立同分布樣本.對(duì)給定的x>0,定義經(jīng)驗(yàn)分布函數(shù)為

容易得到經(jīng)驗(yàn)分布函數(shù)的期望和方差為

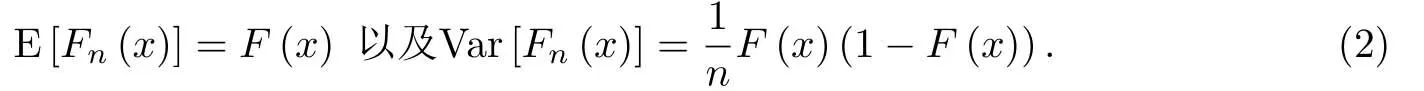
因此Fn(x)是F(x)的無偏相合估計(jì).

注意到密度函數(shù)是分布函數(shù)的導(dǎo)數(shù),根據(jù)導(dǎo)數(shù)的定義有

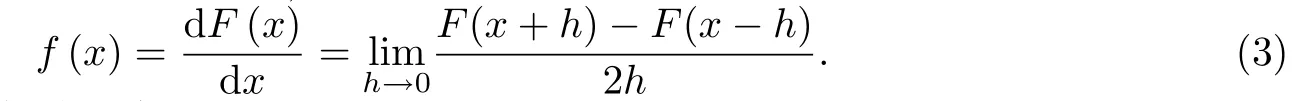
容易想到f(x)的一個(gè)近似估計(jì)為

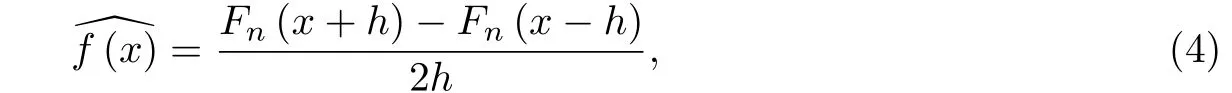
其中h是一個(gè)給定的小的正數(shù).如果令

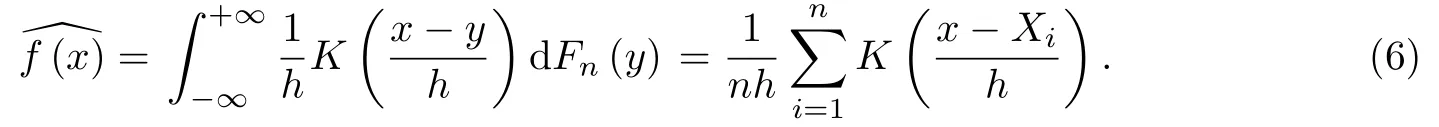
其中K(y)被稱為核函數(shù).進(jìn)一步地,令Kh(·)=K(·/h)/h.記

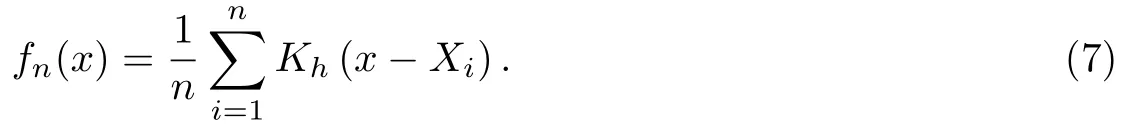
當(dāng)K(y)不取為(5)式而取更一般的核函數(shù)時(shí),估計(jì)(7)被稱為核密度估計(jì)或核估計(jì).其中h被稱為窗寬.

首先容易證明核密度估計(jì)fn(x)是漸近無偏估計(jì)[11],即有

一般地,窗寬h的選取與樣本容量n有關(guān),且有對(duì)于核函數(shù)K(y),常常選取偶函數(shù)且滿足:.常用的核函數(shù)有均勻核,高斯核,三角核以及Epanechikov核等.

在信度理論中,保單的損失額度X常常是連續(xù)型隨機(jī)變量,具有某個(gè)概率密度函數(shù)f(x;θ),其中θ一般表示該風(fēng)險(xiǎn)的特征.例如,在汽車第三者責(zé)任保險(xiǎn)中,θ為汽車的型號(hào),行駛里程數(shù),司機(jī)的年齡,性別,工作性質(zhì)等與風(fēng)險(xiǎn)相關(guān)的綜合因素總和.由于保單的非齊次性,θ一般為隨機(jī)變量,具有某個(gè)先驗(yàn)分布π(θ).

在保險(xiǎn)合同中,被保險(xiǎn)人通過繳納一定的保費(fèi)將風(fēng)險(xiǎn)X轉(zhuǎn)嫁給保險(xiǎn)公司.顯然,保費(fèi)的多少是該保單合同成立的關(guān)鍵.精算師通過分析X的分布,通過某種方法確定風(fēng)險(xiǎn)X保費(fèi).這種確定保費(fèi)的方法稱之為保費(fèi)原理.

定義1.1設(shè)X為非負(fù)隨機(jī)變量,具有密度函數(shù)f(x;θ).保費(fèi)原理即為對(duì)風(fēng)險(xiǎn)X分配一個(gè)固定的數(shù)額H(X),記為X 7?→H(X)或f(x;θ)7?→H(f(x;θ)).

在實(shí)際中,常用的保費(fèi)原理有期望值原理,方差原理,標(biāo)準(zhǔn)差原理,Esscher保費(fèi)原理,指數(shù)保費(fèi)原理等等.關(guān)于保費(fèi)原理的詳細(xì)介紹可參考[16].經(jīng)典的信度理論僅給出了凈保費(fèi)原理的經(jīng)驗(yàn)厘定方法.近年來,已有許多文獻(xiàn)討論各種保費(fèi)原理下風(fēng)險(xiǎn)保費(fèi)的經(jīng)驗(yàn)厘定問題.大部分研究都是通過將平方損失函數(shù)修改為其他損失函數(shù)的方法,獲得某些特殊的保費(fèi)原理中風(fēng)險(xiǎn)保費(fèi)的信度估計(jì)及其經(jīng)驗(yàn)厘定[7,9-10].然而,對(duì)于某些保費(fèi)原理,例如方差保費(fèi)原理,標(biāo)準(zhǔn)差保費(fèi)原理,分位數(shù)保費(fèi)原理,它們不能通過修改損失函數(shù)的方法得到.注意到,不管是什么保費(fèi)原理,總能表達(dá)為密度函數(shù)的某個(gè)泛函H(f(x;θ)).如果能獲得密度函數(shù)的信度估計(jì),則通過代入的方法即可獲得該保費(fèi)原理中風(fēng)險(xiǎn)保費(fèi)的信度估計(jì),即為

因此,下一節(jié)將探討密度函數(shù)的信度估計(jì)問題.

§3 基于核函數(shù)下密度函數(shù)的信度估計(jì)

考慮一個(gè)保單合同,被保險(xiǎn)人面臨的可能損失為X.在風(fēng)險(xiǎn)參數(shù)θ給定條件下,風(fēng)險(xiǎn)X的密度函數(shù)為f(x;θ).由于風(fēng)險(xiǎn)的非齊次性,假設(shè)風(fēng)險(xiǎn)參數(shù)θ為隨機(jī)變量,服從某個(gè)先驗(yàn)分布π(θ).設(shè)(X1,···,Xn)分別為該風(fēng)險(xiǎn)在n個(gè)保單期的索賠樣本.本文的目的是根據(jù)樣本信息和先驗(yàn)信息估計(jì)條件密度函數(shù)f(x;θ),進(jìn)而估計(jì)風(fēng)險(xiǎn)X的保費(fèi)H(f(x;θ)).

根據(jù)Bayes定理,對(duì)給定的x>0,條件密度函數(shù)f(x;θ)的后驗(yàn)均值

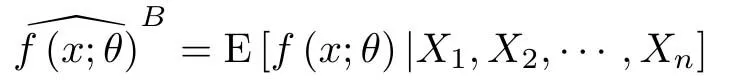
是平方損失函數(shù)下f(x;θ)的最優(yōu)估計(jì),即有

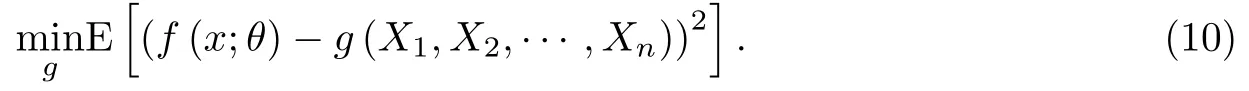
§4 基于密度函數(shù)的信度估計(jì)的保費(fèi)厘定

表1 當(dāng)樣本容量n=10的均方誤差及估計(jì)效率

表2 當(dāng)樣本容量n=50的均方誤差及估計(jì)效率

模擬結(jié)果表明,在窗寬較小的情況下,即使小樣本容量也能保證估計(jì)有較小的均方誤差,隨著樣本容量增大,估計(jì)的效率很快收斂到1.