范振成

(閩江學(xué)院數(shù)學(xué)與數(shù)據(jù)科學(xué)學(xué)院,福建福州350108)

§1 引 言

在芯片(大規(guī)模集成電路)設(shè)計(jì)領(lǐng)域,仿真計(jì)算作用重大.描述芯片的數(shù)學(xué)模型一般是超高維的微分代數(shù)方程組,使用諸如線性多步法和Runge-Kutta方法等經(jīng)典數(shù)值方法進(jìn)行仿真計(jì)算時(shí),因其計(jì)算量太大,效果不理想.描述芯片的高維微分代數(shù)方程組,一般是由若干聯(lián)系微弱的小方程組構(gòu)成,針對(duì)這個(gè)特點(diǎn),基于解代數(shù)方程組的迭代法,Lelarasmee等提出了解微分方程的波形松弛方法[1],其基本想法是先利用迭代技術(shù)將大系統(tǒng)分成若干獨(dú)立的小系統(tǒng),然后根據(jù)各小系統(tǒng)的特點(diǎn)選用適合的經(jīng)典數(shù)值方法進(jìn)行求解計(jì)算.與經(jīng)典方法相比,波形松弛方法因具有并行性和多速率兩個(gè)優(yōu)點(diǎn),而更具優(yōu)勢(shì).在物理,電子,生物等領(lǐng)域,事物將來(lái)的狀態(tài)往往不僅與現(xiàn)在狀態(tài)有關(guān),而且受過(guò)去狀態(tài)影響,此時(shí)泛函微分方程是更理想的模型.研究泛函微分方程的波形松弛方法是必要的.

考慮泛函微分方程(FDEs)

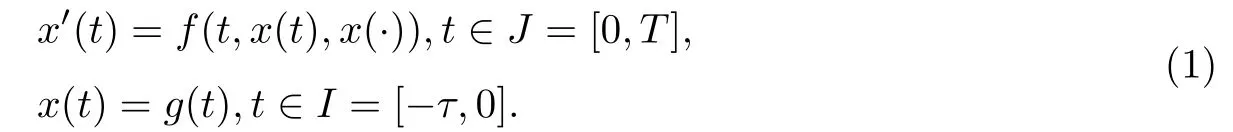
取分裂函數(shù)F(t,x,x,y(·))=f(t,x,y(·)),令x0(t)是(1)精確解x(t)的初始近似,滿足x0(t)=g(t),t∈I.建立迭代格式

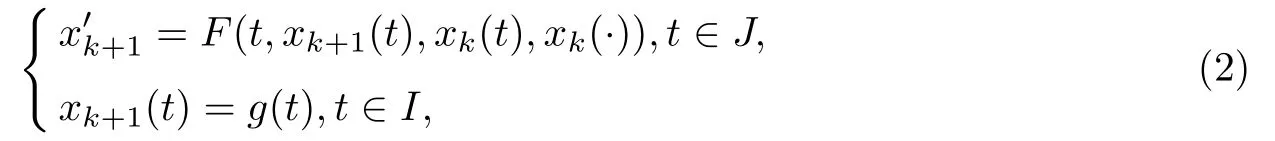
由此可得x(t)的近似解序列{{xk(t):t∈I∪J},k=0,1,2,···},稱此方法為(1)的波形松弛方法.

[2]考慮延遲微分方程(一種特殊的泛函微分方程)的波形松弛方法

假設(shè)分裂函數(shù)F(xk+1(t),xk(t),xk(θ(t)))關(guān)于括號(hào)里第一項(xiàng)滿足單邊Lipschitz條件,關(guān)于第二三項(xiàng)滿足全局Lipschitz條件,在這兩個(gè)條件下,利用內(nèi)積的性質(zhì),得到了波形松弛解和對(duì)應(yīng)準(zhǔn)確解的差的不等式,在此基礎(chǔ)上證明了波形松弛方法是超線性收斂的.[3-5]研究泛函微分方程(2)的收斂性.在分裂函數(shù)F關(guān)于xk+1(t)滿足單邊Lipschitz條件,關(guān)于xk(t)和xk(·)滿足全局Lipschitz條件時(shí),部分借鑒[2]的方法,文獻(xiàn)[3]證明了(2)是收斂的,文獻(xiàn)[4]得到了(2)生成的近似解的誤差估計(jì),該估計(jì)揭示了延遲和誤差的的關(guān)系.文獻(xiàn)[5]針對(duì)分裂函數(shù)F滿足線性和非線性條件,和推廣的依賴時(shí)間的Lipschitz條件兩種情況,得到了新的誤差估計(jì),并從不同的角度與全局Lipschitz條件下的誤差估計(jì)進(jìn)行了比較.

近些年,圍繞收斂性,泛函微分方程波形松弛方法的研究工作持續(xù)推進(jìn).如推廣到中立型泛函微分方程,分?jǐn)?shù)階泛函微分方程,隨機(jī)泛函微分方程等,參見(jiàn)[6-12].

在(2)的計(jì)算過(guò)程中,誤差不可避免.如果初始值或分裂函數(shù)的微小改變,將引起解的劇烈變動(dòng),即方法不穩(wěn)定,則方法沒(méi)有意義.目前罕見(jiàn)關(guān)于(2)穩(wěn)定的研究工作.考慮(2)的擾動(dòng)系統(tǒng)

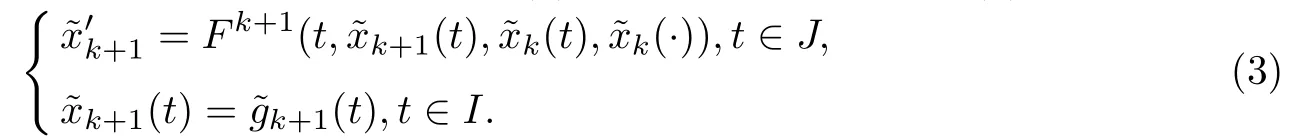
其中Fk+1≈F,k+1≈g,0≈x0.[3]研究了(2)和(3)的解的關(guān)系,證明了在某些條件下,當(dāng)k→∞,Fk+1→F,k+1→g時(shí),k→x.此結(jié)果說(shuō)明了在某些條件下,初始值和分裂函數(shù)的微小改變不會(huì)引起解的劇烈變化,據(jù)作者所知這是唯一的與(2)穩(wěn)定性相關(guān)的工作.

本文借鑒文獻(xiàn)[2-4]提出的技術(shù),研究(2)的穩(wěn)定性.分析波形松弛方法(2)和它的擾動(dòng)系統(tǒng)(3)的解的差,利用[2-4]的方法,推導(dǎo)得出了k?xk的估計(jì)式,進(jìn)而根據(jù)該估計(jì)得到(2)的穩(wěn)定條件,改進(jìn)了[3]的結(jié)果.

§2 主要結(jié)果

這說(shuō)明了推論2.1改進(jìn)了[3]的結(jié)果.

§3 定理的證明

§4 數(shù)值算例

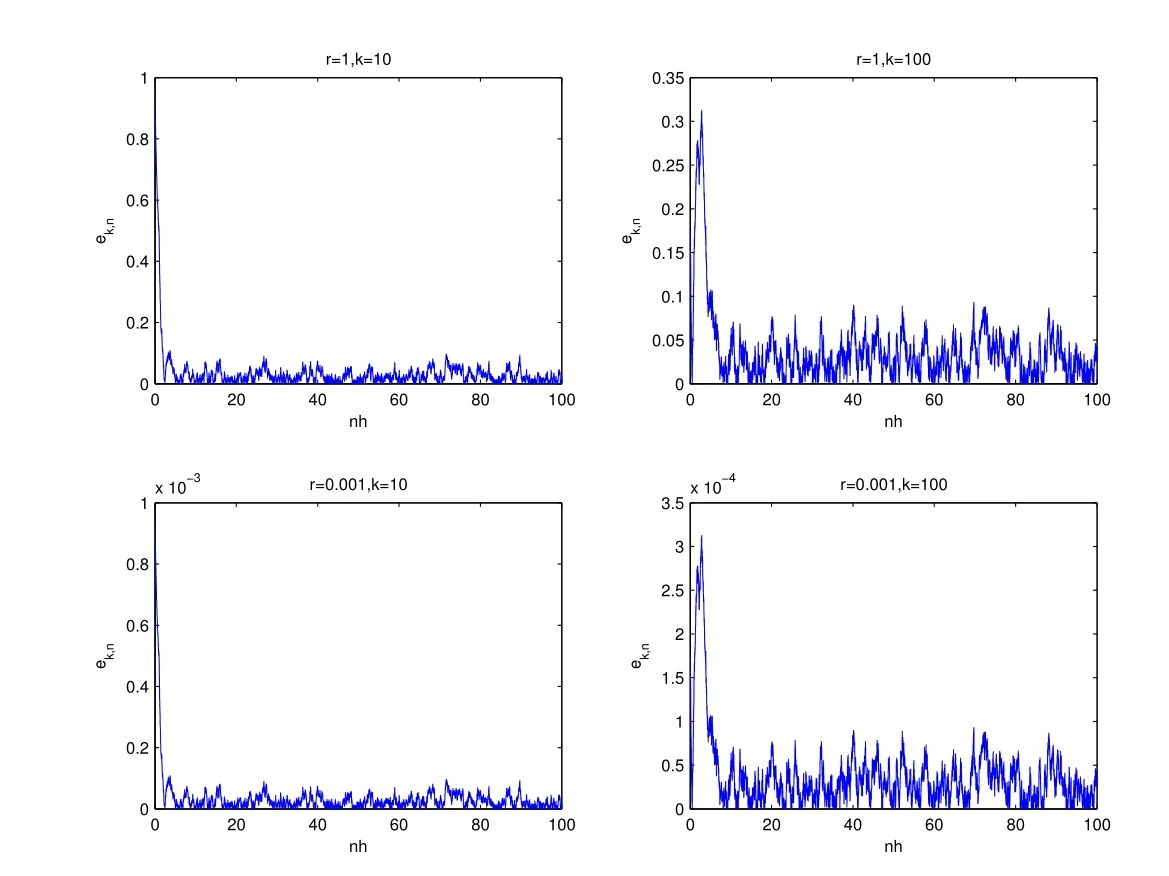
圖1 波形松弛方法(25)與其擾動(dòng)系統(tǒng)(26)的解的差

如果(25)中初始值和右端函數(shù)發(fā)生小的改變,則得到擾動(dòng)系統(tǒng)

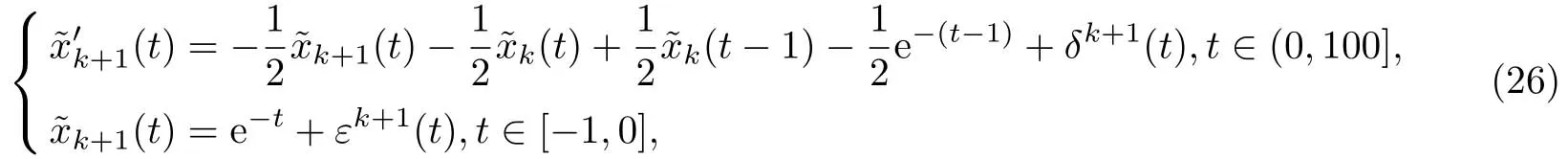
其中k=0,1,···,0(t)=x0(t)+ε0(t),對(duì)t∈[?1,100].

使用步長(zhǎng)h=0.01的改進(jìn)Euler方法(2階Runge-Kutta方法)分別求(25)和(26)在節(jié)點(diǎn)tn=nh,n=?1/h,?1/h+1,···,100/h的近似解{xk,n}和{k,n}.如果兩個(gè)近似解的差有界,則(25)穩(wěn)定,否則(25)不穩(wěn)定.為了滿足(H3)-(H5)并盡可能接近實(shí)際情況,取δk(tn)=rξk,n,εk(tn)=rζk,n,這里{ξk,n,ζk,n}是相互獨(dú)立的服從U(?1,1)(區(qū)間(-1,1)上的均勻分布)的隨機(jī)變量序列,r是一個(gè)正常數(shù).記ek,n=|k,n?xk,n|,在圖1中分別畫(huà)出了k=10,r=1,k=10,r=0.01,k=100,r=1和k=100,r=0.001時(shí)(25)和(26)的解的差{ek,n}.結(jié)果表明波形松弛方法(25)是穩(wěn)定的.

§5 結(jié)論

假設(shè)泛函微分方程波形松弛方法的初始值和每一步計(jì)算都有微小擾動(dòng),分析了生成的擾動(dòng)系統(tǒng)的解的變化情況,得出了擾動(dòng)系統(tǒng)和原系統(tǒng)的解的差的估計(jì)式.該估計(jì)說(shuō)明,在很一般的條件下擾動(dòng)系統(tǒng)的解變化不大,即波形松弛方法有較強(qiáng)的抗干擾能力.改進(jìn)了文獻(xiàn)[3]的結(jié)果.文中提出的收斂穩(wěn)定不同于絕對(duì)穩(wěn)定,A穩(wěn)定等常見(jiàn)數(shù)值近似方法的穩(wěn)定,更接近零穩(wěn)定.眾所周知收斂蘊(yùn)含零穩(wěn)定,目前尚不清楚收斂是否一定收斂穩(wěn)定.以后將繼續(xù)研究二者的關(guān)系.