安徽省靈璧師范學校(234200)陳 偉

在基本不等式中,常常會涉及到兩個變量等式,求這兩個變量的積或線性和的取值范圍問題.本文結合具體實例探究這類問題的基本解題思路.

例1已知x＞0,y＞0且,求x+y的取值范圍.

解法1(常值代換)

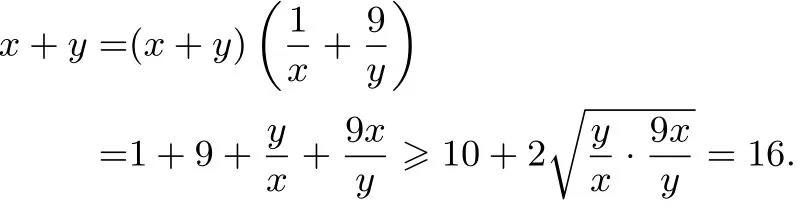
點評如果已知兩個正數(shù)和為定值,求其倒數(shù)的線性和的取值范圍問題,基本的解題思路是常值代換法,展開利用基本不等式求解.

解法2(化為一元函數(shù))由x＞0,y＞0且知,

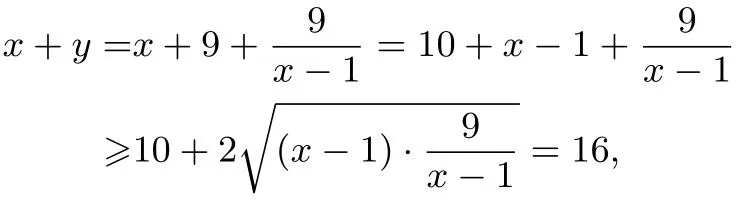
點評這種解法運用函數(shù)與方程思想,把二元問題轉化為一元函數(shù),可以用基本不等式,也可以用導數(shù)解決.

解法3(判別式)設x+y=t,y=t-x代入整理得x2+(t-8)x+t=0,關于x的一元二次方程有解,于是Δ=(t-8)2-4t=t2-20t+64=(t-4)(t-16)≥0,所以t≤4或t≥16,又由x＞1,y＞9知t≥16,所以x+y的取值范圍是[16,+∞).

點評用到換元的思想方法,把問題轉化成一元二次方程,用判別式來解決,最后還得結合條件進行取舍.這也是解決這類問題常用的方法.

解法4(配湊法)由知x＞1,y＞9,變形得x+y≥16,所以x+y的取值范圍是[16,+∞).

點評這種解法需要對表達進行恰當變形,技巧性較強.

解法5(數(shù)形結合)

由x＞0,y＞0且知.平移直線x+y=0且與曲線y=9)相切時x+y取得最小值.令得x=4,求得y=12時,此時x+y取得最小值16,所以x+y的取值范圍是[16,+∞).

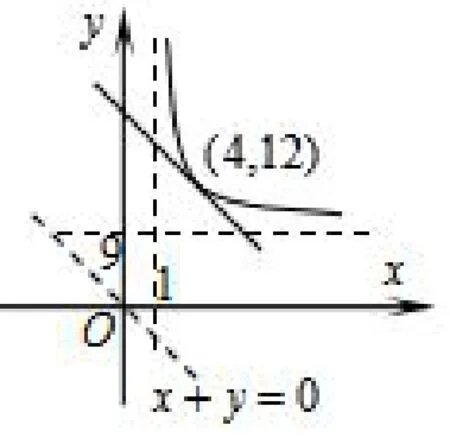
圖1

點評轉化成在約束條件下目標函數(shù)的取值范圍問題,數(shù)形結合運用線性規(guī)劃的基本思想方法.

解法6(向量法(柯西不等式))由于x＞0,y＞0,設向量,則.又由a·b=|a|·|b|cos〈a,b〉得1+3=,所以x+y≥16.當且僅當向量a與b同向,即x=4,y=12時,x+y取得最小值16,所以x+y的取值范圍是[16,+∞).

點評這種解法是根據(jù)條件構造兩個向量用數(shù)量積來求解,實際上是柯西不等式.

變形1已知x＞0,y＞0且.若a,b是正常數(shù),求ax+by的取值范圍.

解(常值代換).當且僅當,即時,ax+by取得最小值,所以ax+by的取值范圍是.

變形2已知實數(shù)x,y,滿足9x+y=xy,求x+y的取值范圍.

解(判別式)設x+y=t,y=t-x代入9x+y=xy整理得x2+(t-8)x+t=0,關于x的一元二次方程有解,于是Δ=(t-8)2-4t=t2-20t+64=(t-4)(t-16)≥0,所以t≤4或t≥16,所以x+y的取值范圍是(-∞,4]∪[16,+∞).

點評這個問題可理解為:在約束條件9x+y=xy下,求目標函數(shù)z=x+y的取值范圍.結合圖形,平移直線x+y=0且與曲線9x+y=xy相切時,即可得到x+y的取值范圍.

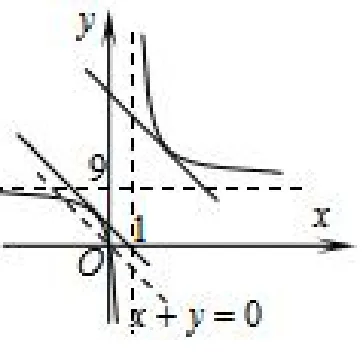
圖2

例2已知x＞0,y＞0且xy=x+y+1,求3x+2y的最小值.

解法1(化為一元函數(shù))由x＞0,y＞0且xy=x+y+1知,

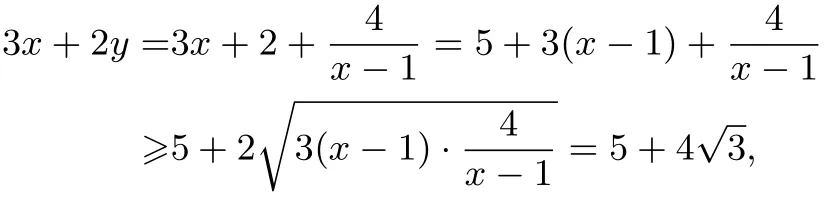
解法2(判別式)設3x+2y=t,代入xy=x+y+1整理得x2-(t+1)x+t+2=0,關于x的一元二次方程有解,于是Δ=(t+1)2-12(t+2)=t2-10t-23≥0,所以或,又由x＞1,y＞1知,當且僅當Δ=0,即,時,所以3x+2y取得最小值.

解法3(配湊法)由xy=x+y+1變形得(x-1)(y-1)=2且x＞1,y＞1,3x+2y=5+3(x-1)+2(y-1)≥5+,當且僅當3(x-1)=2(y-1),即時,3x+2y取得最小值.

注(1)本題可以求出3x+2y取值范圍是[5+.(2)本題也可用線性規(guī)劃的基本思想方法求解.

例3已知x＞0,y＞0且x+2y+xy=30,求xy的最大值.

解法1(基本不等式)由x+2y+xy=30得,得,即0＜xy≤18,當且僅當x=2y,即x=6,y=3時,xy取得最大值18.

解法2(化為一元函數(shù))由x＞0,y＞0且x+2y+xy=30知,當且僅當,即x=6,y=3時,xy取得最大值18.

解法3(判別式)設xy=t,,代入x+2y+xy=30整理得x2+(t-30)x+2t=0,關于x的一元二次方程有解,于是Δ=(t-30)2-8t=t2-68t+900=(t-18)(t-50)≥0,所以t≤18或t≥50,又由0＜x＜30,0＜y＜15知t≤18,當且僅當Δ=0,即x=6,y=3時,xy取得最大值18.

注本題可以求出xy的取值范圍是(0,18].

在解題過程中,嘗試不同的視角分析解決同一個問題,可以強化知識間的聯(lián)系,提高學生運用知識分析問題和解決問題的能力.