陳玉明 陳春濤

(1.廣東技術(shù)師范學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院, 廣州 510665)(2.廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院, 南寧 530004)

引言

在1963年,Lorenz提出了首個混沌數(shù)理模型, 即Lorenz系統(tǒng)[1],這個系統(tǒng)起源于大氣模型之中. 自此以后, 來至不同領(lǐng)域的數(shù)學(xué)家, 物理學(xué)家及工程師們對混沌的產(chǎn)生,混沌系統(tǒng)的特征, 分岔及通向混沌的路徑等方面進(jìn)行了深入的研究[2-5].

超混沌, 作為另一種復(fù)雜動力學(xué)行為, 它比混沌行為具有更強(qiáng)的復(fù)雜性, 并且在非傳統(tǒng)工業(yè)及技術(shù)領(lǐng)域具有更強(qiáng)的應(yīng)用潛力. 由于在自治常微分方程系統(tǒng)中要產(chǎn)生超混沌行為, 必須要求系統(tǒng)維數(shù)至少為四維, 因此, 對四維超混沌系統(tǒng)的研究, 尤其是對四維Lorenz型超混沌系統(tǒng)的研究[6,7],將顯得尤為重要.

在三維混沌系統(tǒng)的研究中, 有很多研究者研究了系統(tǒng)平衡點(diǎn)的Zero-Hopf分岔現(xiàn)象,例如Guckenheimer[8], Han[9], Kuznetsov[10]及Llibre[11]等等. 從這些文獻(xiàn)的研究可以看出,在一定的條件下, 從局部的Zero-Hopf平衡點(diǎn)處可以分岔出一些復(fù)雜的不變集, 也就是說, 在某些情況下, Zero-Hopf平衡點(diǎn)的出現(xiàn)便意味著“混沌”的產(chǎn)生. 在四維超混沌系統(tǒng)的研究中, 最近Cid-Montiel及Llibre等研究了一類超混沌Lorenz系統(tǒng)的Zero-Hopf分岔行為[12], 這是在中心流形維數(shù)大于等于4的系統(tǒng)中關(guān)于Zero-Hopf平衡點(diǎn)及分岔的首個工作. 即便到現(xiàn)在, 這類研究工作在四維及四維以上的系統(tǒng)中依然屬于非常罕見.

混沌及超混沌系統(tǒng)的復(fù)雜性主要來源于混沌及超混沌吸引子的存在. 一般情形下, 相空間中只存在一個穩(wěn)定的吸引子, 除了其它吸引子(都為不穩(wěn)定)本身外, 從相空間中其它點(diǎn)出發(fā)的軌線都將趨向于那唯一的一個穩(wěn)定的吸引子. 然而一些研究者最近發(fā)現(xiàn)了很多特殊的系統(tǒng)[14,15], 在這些系統(tǒng)中存在著各種不同穩(wěn)定吸引子的共存現(xiàn)象, 這使得系統(tǒng)的相空間變得異常復(fù)雜, 尤其是這些不同穩(wěn)定吸引子的吸引盆的邊界.

通過對經(jīng)典的Lorenz系統(tǒng)添加反饋控制, 本文得到如下的四維Lorenz型系統(tǒng):

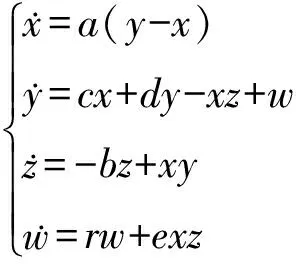
(1)

其中參數(shù)滿足a>0,b>0,cder≠0. 當(dāng)系統(tǒng)參數(shù)選取a=27.7,b=3.8,c=29.2,d=-1.5,e=-1.6及r=1.4時, 系統(tǒng)(1)具有超混沌吸引子, 該吸引子所對應(yīng)的Lyapunov指數(shù)為:

λLE1=0.4157,λLE2=0.2479,λLE3=-0.0002,

λLE4=-32.2601.

該超混沌吸引子在x-y-z空間的投影相圖如圖1所示.

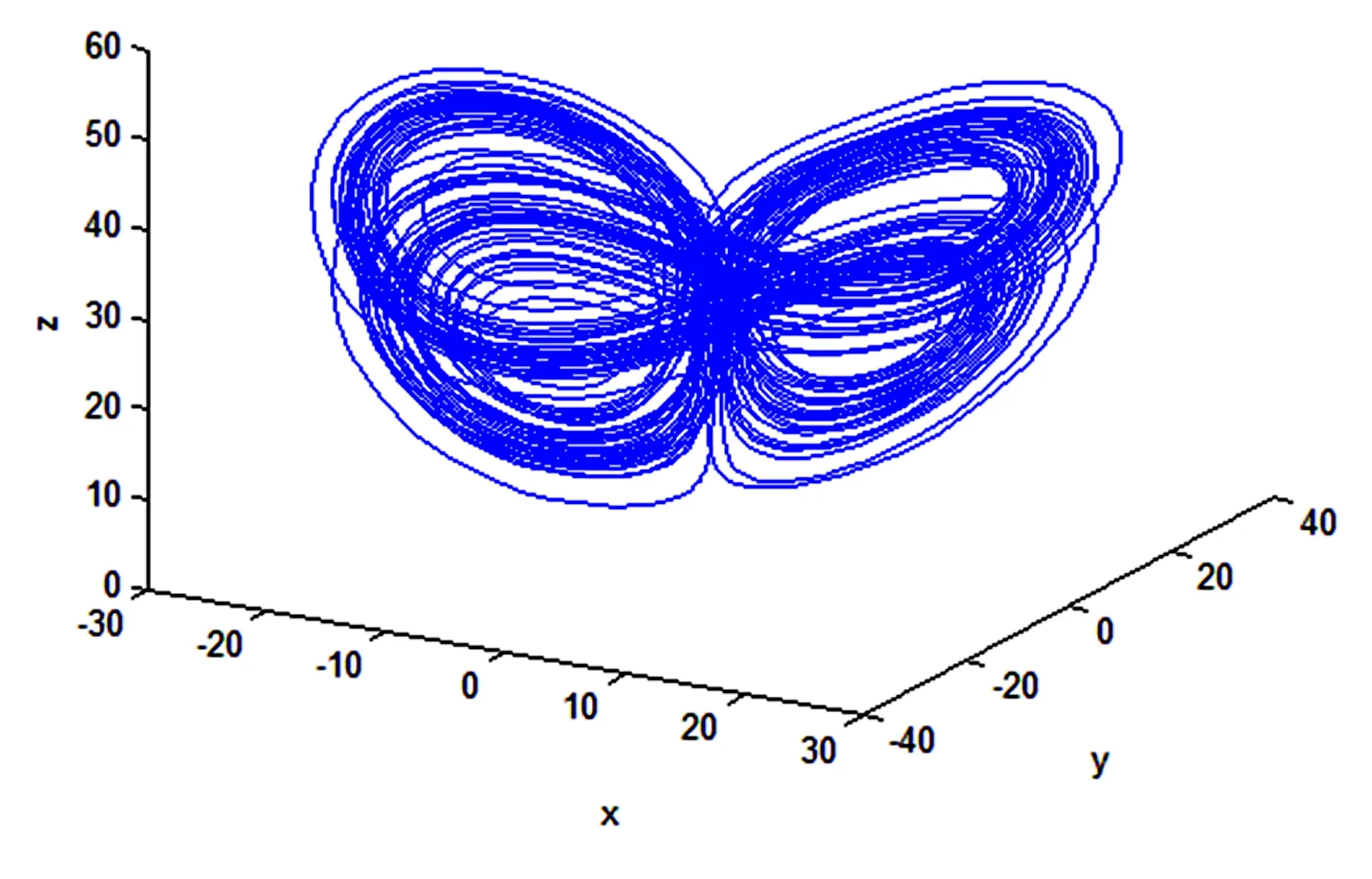
圖1 系統(tǒng)(1)的超混沌吸引子在x-y-z空間的投影相圖a=27.7,b=3.8,c=29.2,d=-1.5,e=-1.6及r=1.4Fig.1 Phase portrait of system (1) in the projection space of x-y-z,where a=27.7,b=3.8,c=29.2,d=-1.5,e=-1.6 and r=1.4

當(dāng)系統(tǒng)參數(shù)滿足br(c+d)(e+r)≤0時,系統(tǒng)(1)只具有唯一平衡點(diǎn)E0(0,0,0,0). 而當(dāng)br(c+d)(e+r)>0時,系統(tǒng)(1)除了具有原點(diǎn)平衡點(diǎn)E0之外, 還將具有另外兩個關(guān)于z軸對稱的非原點(diǎn)平衡點(diǎn).

針對四維Lorenz型超混沌系統(tǒng)(1),本文將研究該系統(tǒng)原點(diǎn)平衡點(diǎn)E0處發(fā)生的Zero-Zero-Hopf分岔行為(所謂Zero-Zer-Hopf平衡點(diǎn), 是指具有兩個零特征值以及一對純虛特征值的孤立平衡點(diǎn)), 以及在某些特定參數(shù)下, 研究系統(tǒng)不同吸引子之間的共存現(xiàn)象.

1 Zero-Zero-Hopf分岔分析

考慮如下形式的微分方程系統(tǒng):

(2)

其中ε∈(-ε0,ε0),ε0是充分小的正數(shù), 函數(shù)F0,F1:R×Ω→Rn以及F2:R×Ω×(-ε0,ε0)→Rn都是C2類函數(shù), 并且關(guān)于它們的第一個變量t都是周期T函數(shù), 其中Ω是Rn中的一個子集. 在平均化理論的幫助下, 我們研究系統(tǒng)(1)中周期解的分岔問題, 其中主要的假設(shè)是未擾動系統(tǒng):

(3)

具有一個周期解流形.

假設(shè)X(t,X0)是系統(tǒng)(3)滿足條件X(0,X0)=X0=X(T,X0)的周期解, 于是系統(tǒng)(3)沿著周期解X(t,X0)的線性化系統(tǒng)可以寫成:

(4)

并且記MX0(t)為線性微分方程(4)的基解矩陣.

假設(shè)存在開集V滿足Cl(V)?Ω, 使得對于任意X0∈Cl(V),都有X(t,X0)為系統(tǒng)(3)中的一個周期為T的周期解. 其中集合Cl(V)被稱為系統(tǒng)(3)的同步集, 這個集合完全是由周期解所構(gòu)成. 包含在同步集Cl(V)中的周期解的分岔問題, 將由如下定理給出.

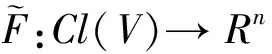
于是有如下結(jié)論成立:

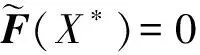
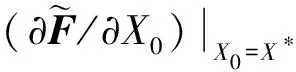
定理2:當(dāng)滿足條件d=a,b=0,r=0及a2+ac<0時, 四維Lorenz型超混沌系統(tǒng)(1)的原點(diǎn)平衡點(diǎn)E0為Zero-Zero-Hopf平衡點(diǎn).

證明:容易計(jì)算得平衡點(diǎn)E0處的特征方程為:

P(λ)=(λ+b)(λ-r)(λ2+aλ-dλ-ac-ad)

(5)

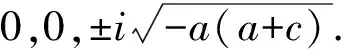
定理3:令D=c(a-d)2e2-2(a+c)(a-d)e(a+e)r-(a+c)(a(a+c)-e2)r2≠0, 則四維Lorenz型超混沌系統(tǒng)(1)在原點(diǎn)平衡點(diǎn)E0處存在Zero-Zero-Hopf分岔. 在條件D1>0,D2>0,D3>0及D4>0下, 當(dāng)原點(diǎn)經(jīng)歷Zero-Zero-Hopf分岔時, 在原點(diǎn)附近將會分岔出兩條穩(wěn)定的周期軌, 其中D1,D2,D3及D4如公式(10)所示.

證明:令ε為充分小的正參數(shù),b1,d1及r1為非零實(shí)數(shù). 在變換(b,d,r)→(εb1,a+εd1,εr1)的作用下,四維Lorenz型超混沌系統(tǒng)(1)將變形為:

(6)

進(jìn)一步對變量進(jìn)行重新標(biāo)度, 令(x,y,z,w)T=(εu,εv,εp,εq)T, 并且將向量(u,v,p,q)T重新記為向量X=(x,y,z,w)T, 于是系統(tǒng)(6)可變?yōu)?

(7)

在定理1所描述的平均化理論的幫助下, 系統(tǒng)(7)的相關(guān)動力學(xué)行為將可以被研究. 考慮如下未擾動系統(tǒng)的初值問題:

(8)

未擾動系統(tǒng)(8)的解為X(t,X0)=(x(t),y(t),z(t),w(t)), 其中:

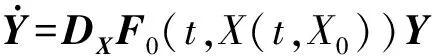
以及它的逆矩陣為:

基于上述矩陣, 計(jì)算定理1中的積分, 可得:

其中:

a(a+c)(x0-y0))z0+(a+c)·

(w0+cx0+ay0)d1-2(a+c)w0r1],

cey0+a(w0-ey0+c(x0+y0)))z0+

(a+c)(2w0+2ay0+c(x0+y0))d1-

2(a+c)w0r1],

2(a+c)2z0b1],

S0=(0,0,0,0),

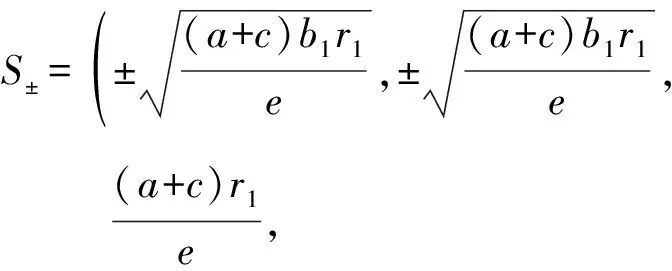
其中解S0對應(yīng)于原點(diǎn)平衡點(diǎn)E0. 針對另外兩個解S±, 有如下關(guān)系式成立:

因此, 根據(jù)定理1, 存在系統(tǒng)(7)的兩個周期為2π/m的周期解X+(t,ε)及X-(t,ε), 使得當(dāng)ε→0時有X+(0,ε)→S+及X-(0,ε)→S-成立. 考慮到系統(tǒng)(6)與系統(tǒng)(7)的關(guān)系, 系統(tǒng)(7)的周期解X±(t,ε)分別對應(yīng)著系統(tǒng)(6)的周期解εX±(t,ε).

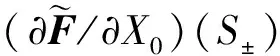
P(S±)=λ4+c1λ3+c2λ2+c3λ+c4

(9)

其中:

2(a+c)e(a2-(2b+d)e+a(e-d))r-

(a+c)(a(a+c)-e2)r2],

令:

D4=c4D3

(10)

根據(jù)Routh-Hurwitz準(zhǔn)則, 在條件D1>0,D2>0,D3>0及D4>0下, 特征多項(xiàng)式(9)的所有根都具有負(fù)實(shí)部, 也就是說, 在原點(diǎn)E0處由Zero-Zero-Hopf分岔所產(chǎn)生的兩個周期解X+(0,ε)→S+及X-(0,ε)→S-都是穩(wěn)定周期解.

2 共存吸引子研究

選取恰當(dāng)?shù)南到y(tǒng)參數(shù), 通過詳細(xì)的數(shù)值分析, 可發(fā)現(xiàn)系統(tǒng)(1)存在多種吸引子共存的現(xiàn)象, 即同組參數(shù)條件下, 系統(tǒng)(1)滿足不同初始條件的解有可能呈現(xiàn)出完全不同的動力學(xué)行為. 具體可包括超混沌吸引子與周期吸引子的共存, 不同周期吸引子之間的共存等.

固定參數(shù)a=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99及r=1.43, 對初始條件(61,68,58,-40), 系統(tǒng)(1)的解將會收斂于一個周期解, 其在y-z-w空間的投影如圖2(a)所示, 該周期吸引子所對應(yīng)的Lyapunov指數(shù)為:λLE1=0.0000,λLE2=-0.0015,λLE3=-0.0015,λLE4=-28.2961.

在同一組參數(shù)下, 對于初始條件(58,55,33,-52), 系統(tǒng)(1)的解則收斂于一個超混沌吸引子, 在y-z-w空間的投影相圖如圖2(b)所示, 該超混沌吸引子所對應(yīng)的Lyapunov指數(shù)為:λLE1=0.2521,λLE2=0.0708,λLE3=0.0000,λLE4=-28.6218.

因此, 當(dāng)參數(shù)滿足a=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99及r=1.43時, 系統(tǒng)(1)的相空間中存在著超混沌吸引子與周期吸引子的共存, 其在y-z-w空間的投影如圖2(c)所示.

類似的, 當(dāng)固定參數(shù)a=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15及r=1.15時, 也存在吸引子的共存現(xiàn)象. 對初始條件(73,-97,3,-73), 系統(tǒng)(1)的解將會收斂于一個周期解, 其在y-z-w空間的投影如圖3(a)所示, 該周期吸引子所對應(yīng)的Lyapunov指數(shù)為:λLE1=0.0000,λLE2=-0.0817,λLE3=-0.4814,λLE4=-32.3287.

在同一組參數(shù)下, 對于初始條件(-57,-82,8,80), 系統(tǒng)(1)的解則收斂于另一個周期吸引子, 在y-z-w空間的投影相圖如圖3(b)所示, 該周期吸引子所對應(yīng)的Lyapunov指數(shù)為:λLE1=-0.0003,λLE2=-0.0535,λLE3=-0.0535,λLE4=-32.7843.

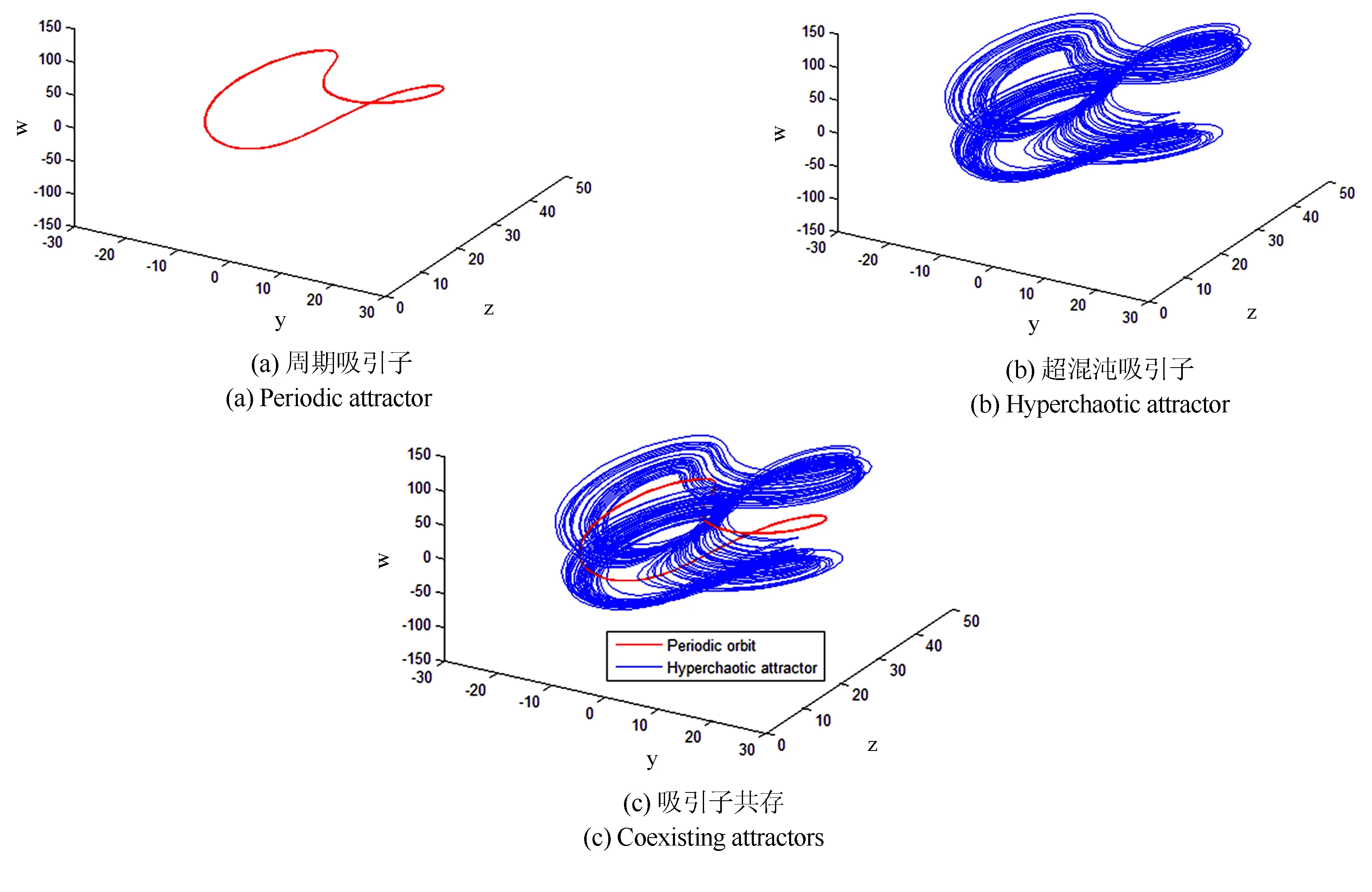
圖2 系統(tǒng)(1)共存吸引子的y-z-w空間投影, a=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99,r=1.43Fig.2 Projections of coexisting attractors in y-z-w space for system(1),wherea=23.96,b=4.39,c=26.82,d=-1.38,e=-0.99,r=1.43

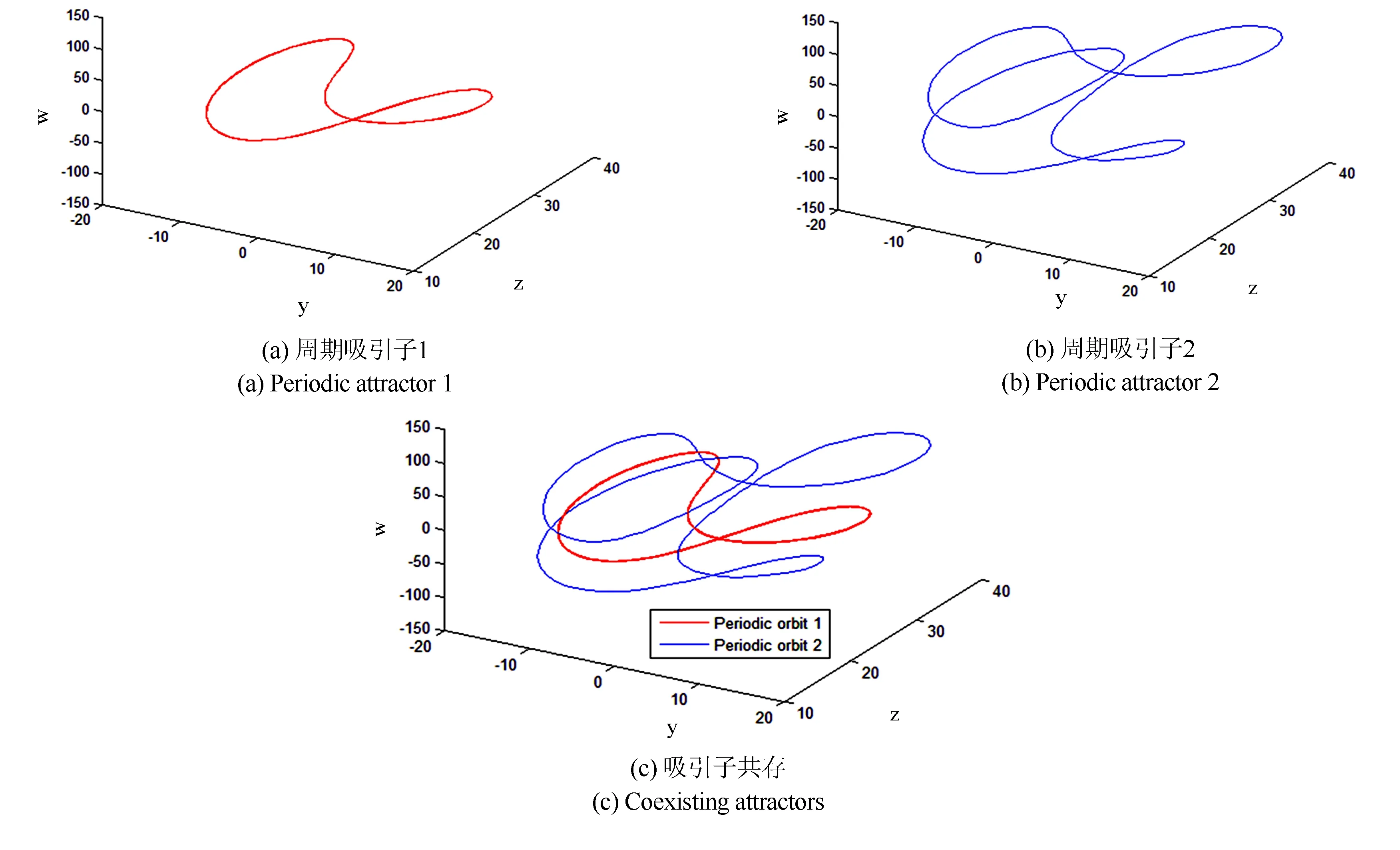
圖3 系統(tǒng)(1)共存吸引子的y-z-w空間投影, a=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15,r=1.15Fig.3 Projections of coexisting attractors in y-z-w space for system(1), wherea=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15,r=1.15

因此, 當(dāng)參數(shù)滿足a=28.67,b=3.52,c=25.16,d=-1.86,e=-1.15及r=1.15時, 系統(tǒng)(1)的相空間中則存在著兩個不同的周期吸引子的共存, 其在y-z-w空間的投影如圖3(c)所示.

3 結(jié)論

通過對經(jīng)典的Lorenz混沌系統(tǒng)施加反饋控制方法, 本文得到了一類四維Lorenz型超混沌系統(tǒng),并從局部和全局兩個方面對該新超混沌系統(tǒng)的動力學(xué)行為進(jìn)行了研究. 首先, 在局部動力學(xué)方面, 基于平均化理論方法, 研究了該系統(tǒng)在原點(diǎn)平衡點(diǎn)處發(fā)生的Zero-Zero-Hopf分岔行為, 得到了系統(tǒng)在原點(diǎn)發(fā)生Zero-Zero-Hopf分岔的參數(shù)條件, 證明了兩條周期軌的存在性, 并且給出了它們的穩(wěn)定性條件. 其次, 在全局動力學(xué)方面, 借助數(shù)值模擬方法, 發(fā)現(xiàn)該系統(tǒng)在某些特定參數(shù)條件下存在著除了平衡點(diǎn)以外的不同吸引子之間的共存現(xiàn)象, 比如超混沌吸引子與周期吸引子共存, 不同周期吸引子之間的共存, 等等.

1Lorenz E N. Deterministic non-periodic flow.JournaloftheAtmosphericSciences, 1963,20:130～141

2Hirsh M W, Smale S, Devaney R L. Differential equations,dynamical systems, and an introduction to chaos. New York:Elsevier Academic Press, 2007

3Shilnikov L P, Shilnikov A L, Turaev D V, et al. Methods of qualitative theory in nonlinear dynamics. Singapore:World Scientific, 2001

4Wiggins S. Introduction to applied nonlinear dynamical systems and chaos(2nd edition). New York:Springer-Verlag, 1990

5Hastings S, Troy W. A shooting approch to chaos in the Lorenz equations.JournalofdifferentialEquations, 1996,127:41～53

6Stenflo L. Generalized Lorenz equations for acoustic-gravity waves in the atmosphere.PhysicaScripata, 1996,53:83～84

7Chen Y, Yang Q. Dynamics of a hyperchaotic Lorenz-type system.NonlinearDynamics, 2014,77:569～581

8Guckenheimer J. On a codimension two bifurcation. In: Lecture Notes in Math, 1980,898:99～142

9Han M. Existence of periodic orbits and invariant tori in codimension two bifurcations of three dimensional systems.JournalofSystemsScienceandMathematicalSciences, 1998,18:403～409

10 Kuznetsov Y A. Elements of applied bifurcation theory(3rd edition). Berlin:Spring, 2004

11 Llibre J, Chavela E P. Zero-Hopf bifurcation for a class of Lorenz-type systems.Discrete&ContinuousDynamicalSystems-SeriesB, 2014,19:1731～1736

12 Montiel L C, Llibre J, Stoica C. Zero-Hopf bifurcation in a hyperchaotic Lorenz system.NonlinearDynamics, 2014,75:561～566

13 周艷,張偉. 復(fù)合材料層合板的雙Hopf分叉分析. 動力學(xué)與控制學(xué)報, 2015,13(3):161～164 (Zhou Y, Zhang W. Double Hopf bifurcation of composite laminated thin plate.JournalofDynamicsandControl, 2015,13(3):161～164(In Chinese))

14 Chen Y, Yang Q. A new Lorenz-type hyperchaotic system with a curve of equilibria.MathematicsandComputersinSimulation, 2015,112:40～55

15 Wei Z. Dynamical behaviors of a chaotic system with no equilibria.PhysicsLettersA, 2011,376:102～108