蔡擇林, 江秉華, 陳金陽, 蔡齊

(1.湖北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,湖北 黃石 435002;2.泰康保險(xiǎn)集團(tuán)股份有限公司稽核中心,湖北 武漢 430000)

混合系數(shù)線性模型的幾乎無偏s-K估計(jì)

蔡擇林1, 江秉華1, 陳金陽1, 蔡齊2

(1.湖北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,湖北 黃石 435002;2.泰康保險(xiǎn)集團(tuán)股份有限公司稽核中心,湖北 武漢 430000)

在連續(xù)測量數(shù)據(jù)情況下,給出了混合系數(shù)線性模型的幾乎無偏s-K估計(jì),討論了該估計(jì)的相關(guān)性質(zhì),并在一定條件下證明了幾乎無偏s-K估計(jì)優(yōu)于s-K估計(jì)以及幾乎無偏嶺估計(jì).

混合系數(shù)線性模型;幾乎無偏s-K估計(jì);s-K估計(jì);幾乎無偏嶺估計(jì);均方誤差

1 引言

考慮如下混合系數(shù)線性模型:

其中

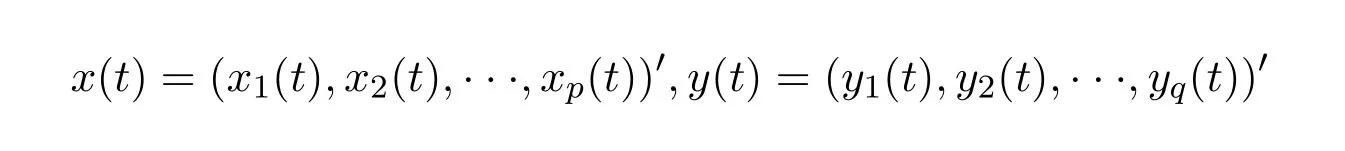
是t的已知向量函數(shù),a是p×1的固定系數(shù)向量,β是q×1的隨機(jī)系數(shù)向量,且β～(b,Σ).現(xiàn)對(duì)m個(gè)樣品,分別在

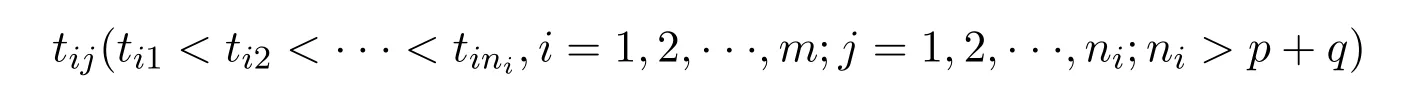
時(shí)測得以下數(shù)據(jù):

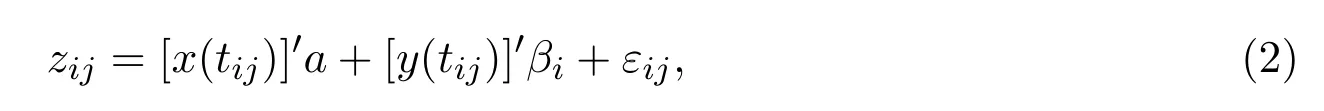
這里的βi和εij分別是每個(gè)樣品的隨機(jī)系數(shù)和每次測量的誤差,βi與εij獨(dú)立,且

若記zi=(zi1,zi2,···,zini)′,εi=(εi1,εi2,···,εini)′,

則可得

式中

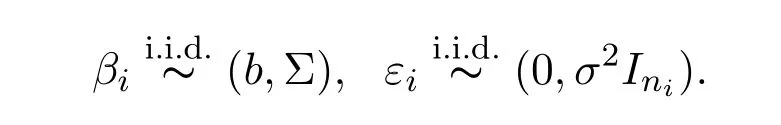
設(shè)

則式(3)變?yōu)?/p>

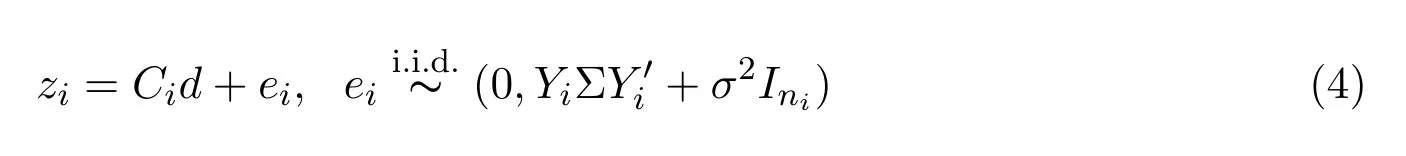
進(jìn)一步,記

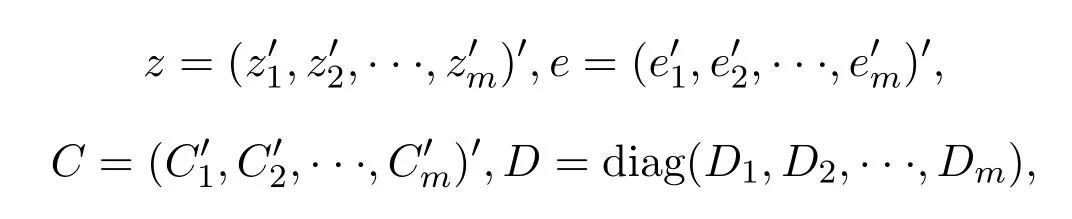
這里p≥0,q≥0.顯然,當(dāng)p=0時(shí)模型化為完全隨機(jī)系數(shù)形式,當(dāng)q=0時(shí)模型化為一般的線性模型.這里還要求

混合系數(shù)線性模型在實(shí)際問題中有著廣泛的應(yīng)用背景,如經(jīng)濟(jì)分析、生物學(xué)等領(lǐng)域.自文獻(xiàn)[1]提出了混合系數(shù)線性模型以后,許多學(xué)者研究了這種模型的參數(shù)估計(jì)[6-10],基于(1.5)式,當(dāng)系數(shù)陣接近病態(tài)時(shí),文獻(xiàn)[2]提出了一種有偏估計(jì):s-K估計(jì).本文提出了LS估計(jì)的一種新的改進(jìn)估計(jì):幾乎無偏s-K估計(jì),在一定條件下證明了幾乎無偏s-K估計(jì)優(yōu)于s-K估計(jì)以及幾乎無偏嶺估計(jì).

2 幾乎無偏s-K估計(jì)

基于(5)式,文獻(xiàn)[1]給出了d的LS估計(jì):?d=(C′C)?1C′Z.(5)式的典則形式為:z=Lr+e,e～(0,D),其中

文獻(xiàn)[2]給出了d的如下s-K估計(jì):

其中s≥1稱為壓縮系數(shù),K=diag(k1,k2,···,kg)≥0稱為嶺參數(shù).

注2.1即為文獻(xiàn)[3]所提出的Stein估計(jì)即為文獻(xiàn)[4]所提出的嶺估計(jì)即為文獻(xiàn)[1]給出的LS估計(jì).

(6)式的典則形式為:

從(7)式容易得到

于是s-K估計(jì)的一個(gè)有偏修正估計(jì)為:

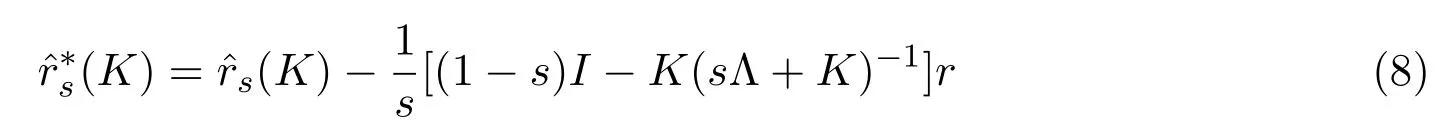
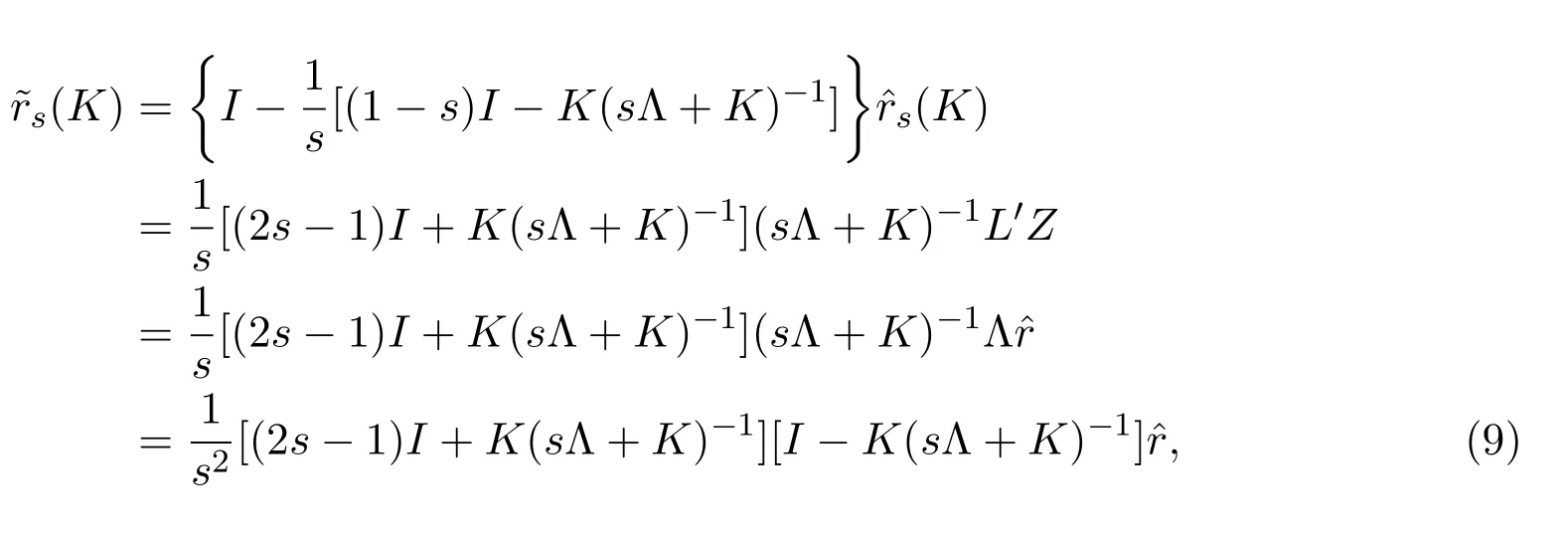
注2.2即為文獻(xiàn)[5]提出的幾乎無偏嶺估計(jì),即為文獻(xiàn)[1]給出的LS估計(jì).

3 幾乎無偏s-K估計(jì)的性質(zhì)

由幾乎無偏s-K估計(jì)的典則形式不難證得:

定理3.1幾乎無偏s-K估計(jì)是壓縮估計(jì),即

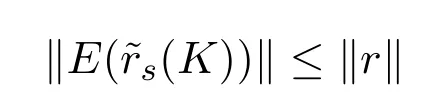
等號(hào)當(dāng)且僅當(dāng)s=1,K=0時(shí)成立.

證明因?yàn)?/p>

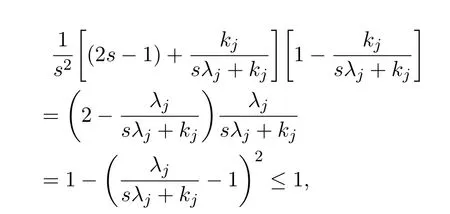
所以

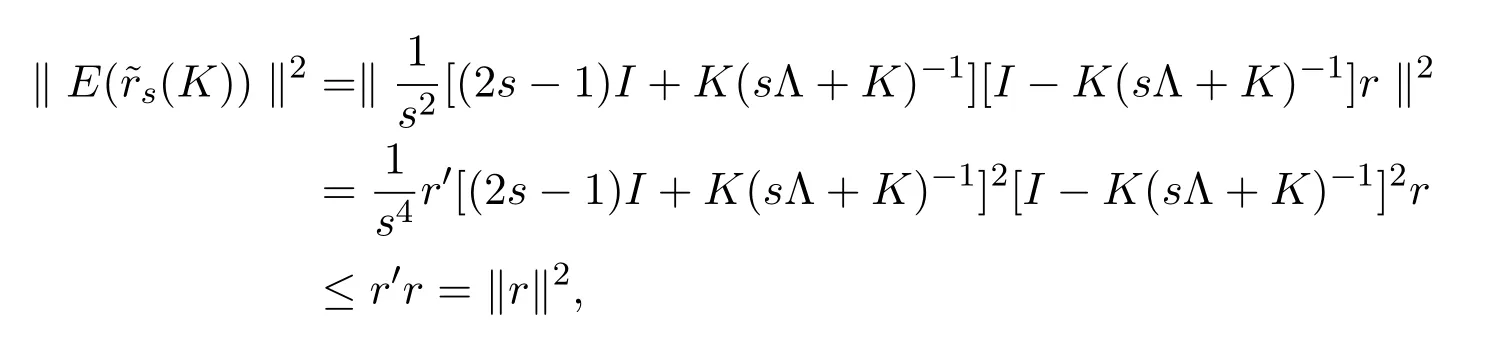
定理 3.2存在s?＞1,K?＞0,對(duì)任意1≤s≤s?,K≥K?使得下式成立.

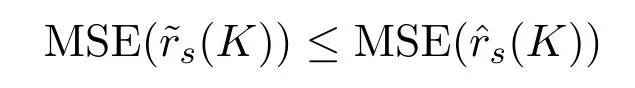
證明顯然

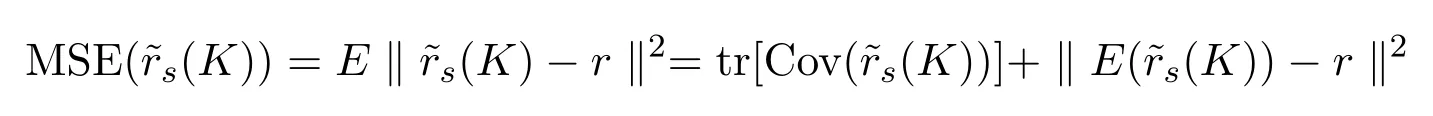
而

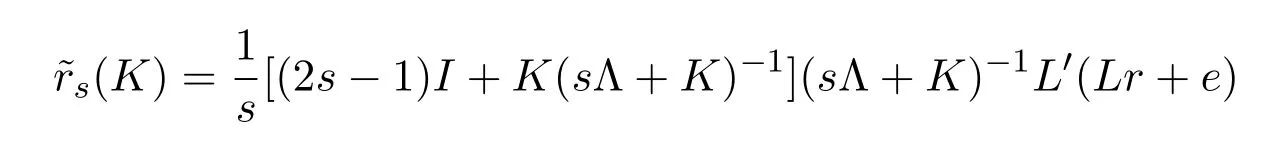
于是

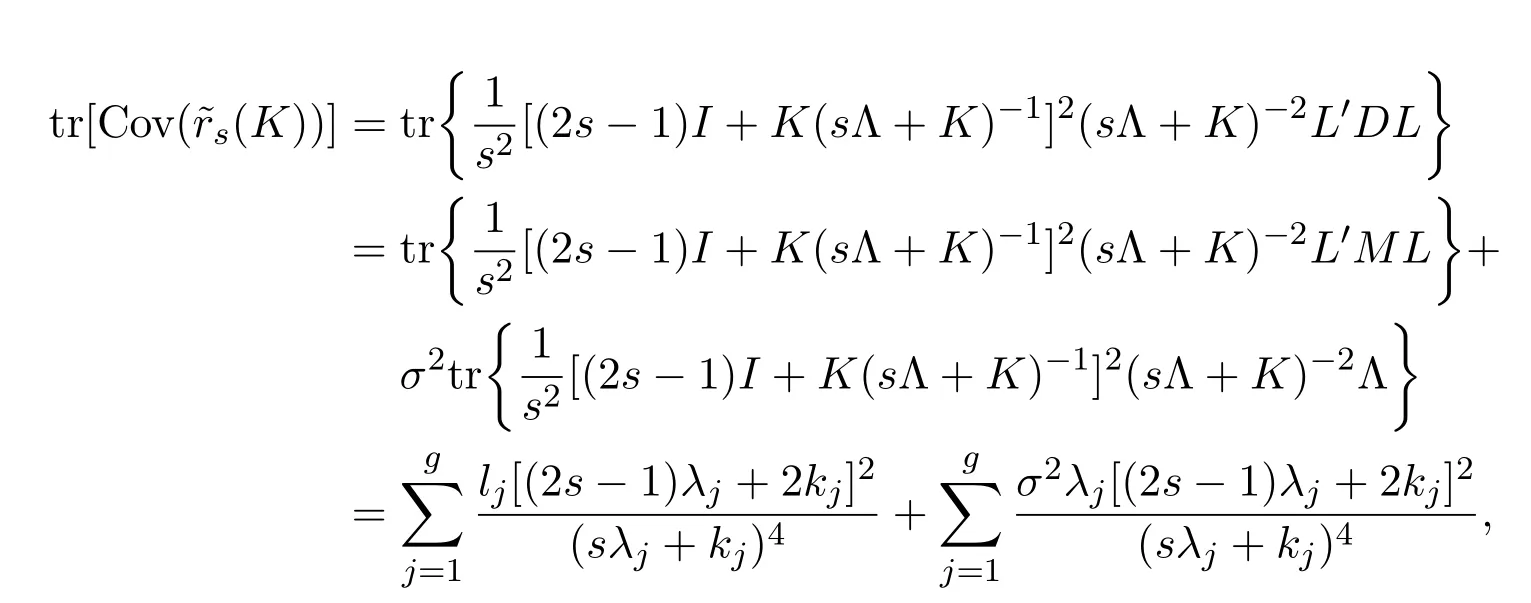
其中

故

而由文獻(xiàn)[2]知,

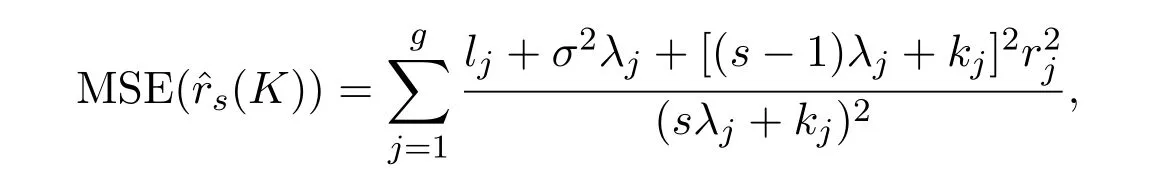
于是

其中

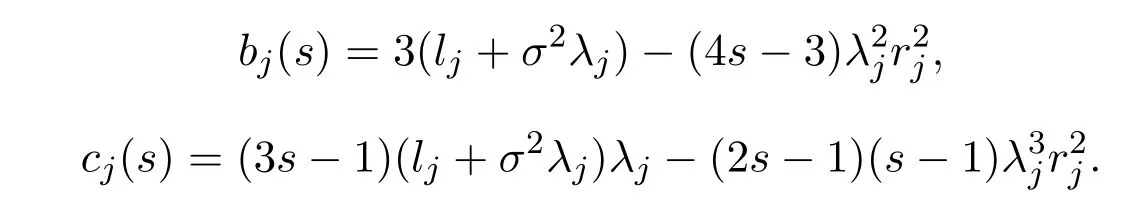
因?yàn)?/p>

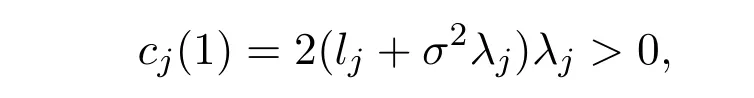
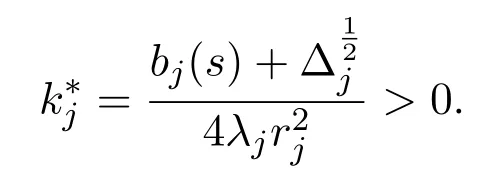
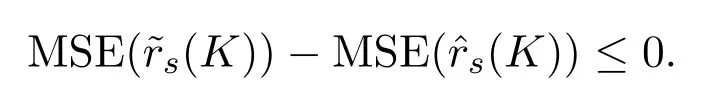
故定理結(jié)論成立.

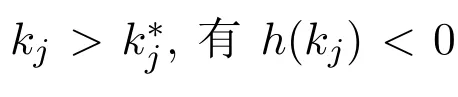
定理 3.3給定K=diag(k1,k2,···,kg),其中

則存在相應(yīng)的s＞1,使得.

證明記

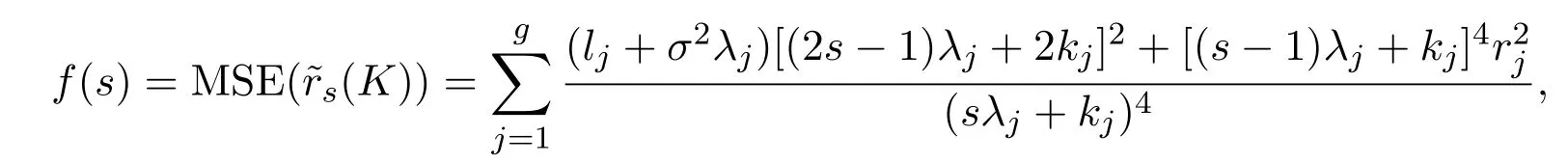
則

令

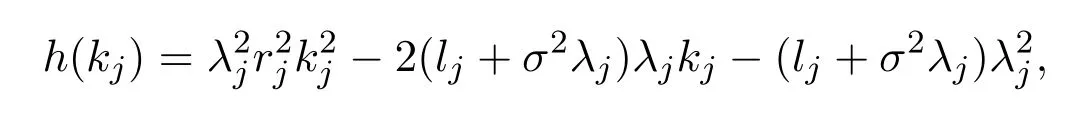
則其判別式和一正根分別為:

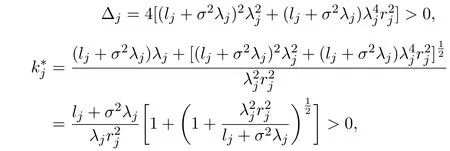
則當(dāng)

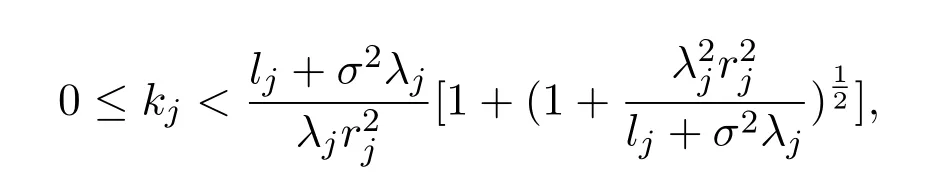
有h(kj)＜0,而K/=0,故f′(1)＜0,又f′(s)為連續(xù)函數(shù),故存在s?＞1,使得f′(s)＜0,s∈[1,s?),即f(s)在 [1,s?)上嚴(yán)格遞減,故f(s)＜f(1),s∈(1,s?).亦即

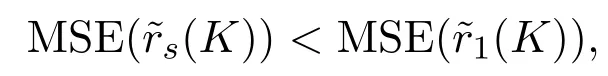
定理結(jié)論成立.

4 數(shù)值模擬

為了進(jìn)一步考察幾乎無偏s-K估計(jì)的均方誤差的表現(xiàn),下面進(jìn)行Monte Carlo數(shù)值模擬.模擬中,取p=1,q=2,m=2,n1=n2=4,且

設(shè)固定系數(shù)a的真實(shí)值為a=0.6,隨機(jī)系數(shù)向量βi～N(b,Σ),i=1,2且β1與β2相互獨(dú)立.其中

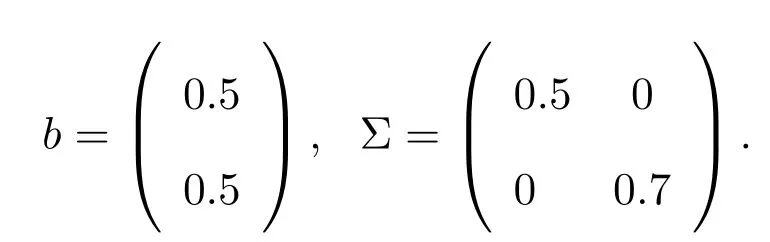
再取隨機(jī)誤差向量εi～N(0,I4),i=1,2且ε1與ε2相互獨(dú)立.試驗(yàn)的重復(fù)次數(shù)取為N=5000.對(duì)于

幾乎無偏嶺估計(jì)(AURE),s-K估計(jì)(s-KE)以及幾乎無偏s-K估計(jì)(AUs-KE)的均方誤差的模擬結(jié)果列在表1中,其結(jié)果進(jìn)一步驗(yàn)證了上文的理論結(jié)果.

表1 三種估計(jì)的均方誤差模擬結(jié)果

[1]莊東辰,茆詩松.混合系數(shù)線性模型的參數(shù)估計(jì)[J].應(yīng)用概率統(tǒng)計(jì),1996,12(1):81-87.

[2]許瑩,何道江.混合系數(shù)線性模型參數(shù)的一類新估計(jì)[J].數(shù)學(xué)物理學(xué)報(bào),2013,33A(4):702-708.

[3]劉小茂,茆詩松.混合系數(shù)線性模型參數(shù)的Stein估計(jì)[J].數(shù)學(xué)物理學(xué)報(bào),2001,21A(4):453-457.

[4]陳靜.混合系數(shù)線性模型參數(shù)的嶺估計(jì)[J].青島大學(xué)學(xué)報(bào),2007,20(2)37-41.

[5]蔡擇林,江秉華.混合系數(shù)線性模型的幾乎無偏嶺估計(jì)[J].數(shù)學(xué)雜志,2013,33(2):354-358.

[6]Rao C R.The theory of least squares when the parameters are stochastic and its application to the analysis of Growth curves[J].Biometrika,1965,52:447-458.

[7]Swamy P A V B.Statistical Inference In random Coefficient Regression Model[M].New York:Springer-Verlage,1971.

[8]Johanson S.Asumptotic inference on random coefficient regression models[J].Scand.J.Statist.,1982,9:201-207.

[9]蔡擇林,江秉華,陳金陽.混合系數(shù)線性模型的一類有偏估計(jì)[J].應(yīng)用數(shù)學(xué),2017,30(3):603-606.

[10]劉小茂,張鈞.混合系數(shù)線性模型參數(shù)的根方估計(jì)[J].華中理工大學(xué)學(xué)報(bào),1997,25(3):111-112.

Almost unbiased s-K estimator for mixed-effect coefficient linear model

Cai Zelin1,Jiang binghua1,Chen Jinyang1,Cai Qi2
(1.College of Mathematics and Statistics,Hubei Normal University,Huangshi435002,China;2.Audit center of Taikang insurance group co.,ltd,Wuhan 430000,China)

Almost unbiased s-K estimator for mixed-effect coefficient linear model is given in the case of repeatedly measured data.Under certain conditions,the new estimators are shown to be superior to the s-K estimators and Almost unbiased ridge estimator,respectively.

mixed-effect coefficient linear model,almost unbiased s-K estimator,s-K estimator,almost unbiased ridge estimator,mean square error

2010 MSC:62J12,62F10

O212.1

A

1008-5513(2017)06-0560-08

10.3969/j.issn.1008-5513.2017.06.002

2017-08-05.

國家自然科學(xué)基金(11471105;71701076);湖北省教育廳青年項(xiàng)目(Q20162504).

蔡擇林(1963-),教授,研究方向:數(shù)理統(tǒng)計(jì).