王秀芝,王如允,曹煒

(寧波大學(xué)數(shù)學(xué)系,浙江 寧波 315211)

有限域上的高斯和與有理點的計算

王秀芝,王如允,曹煒

(寧波大學(xué)數(shù)學(xué)系,浙江 寧波 315211)

設(shè)f是有限域Fq上的n元m項多項式,為其次數(shù)矩陣,用N(f)表示由超曲面f=0在仿射空間 An(Fq)確定的Fq-有理點的個數(shù).若矩陣A∈Zn×m在環(huán) Z/(q?1)Z中與Df行等價,則記為.本文利用高斯和給出了當(dāng)m≤n且,其中λi∈{1,3}時N(f)的具體表達式,從而推廣了已知結(jié)論.

有限域;有理點;特征和;高斯和

1 引言

設(shè)Fq是含有q個元素的有限域,其中q=ph,h≥1,p是一個素數(shù).對于n元非零多項式

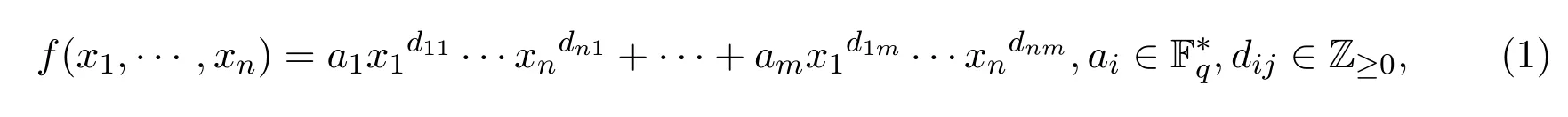
其次數(shù)矩陣定義為n×m階矩陣Df=(D1,···,Dm),其中Dj=(d1j,···,dnj)T,j=1,···,m.多項式f的增廣矩陣定義為,其中.用N(f)表示由超曲面f=0在仿射空間An(Fq)確定的Fq-有理點的個數(shù),即

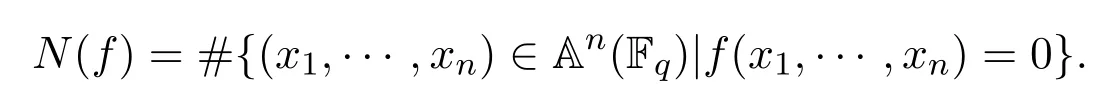
尋找N(f)的表達式在有限域研究中具有重要意義．但要得到N(f)在一般情形下的表達式是很困難的,通常要進行一些適當(dāng)?shù)南拗?參見文獻[1-2]).當(dāng)Df＞0,即Df中的元素均為正整數(shù)時,孫琦得到了下列結(jié)論.

定理1.1[3]設(shè)f為形如(1)的多項式,其中Df＞0.若m=n且gcd(det(Df),q?1)=1,則對于任意的b∈Fq,有

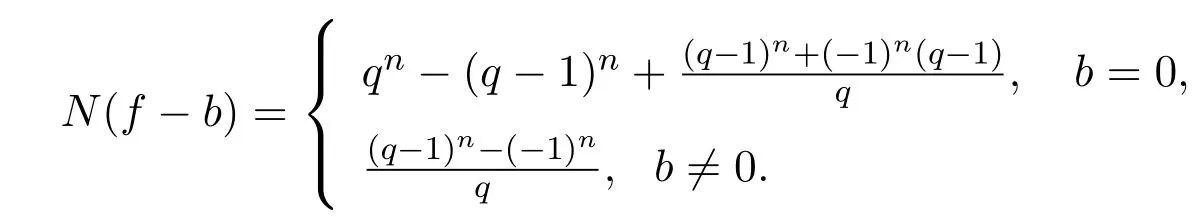
在文獻[4]中,曹煒和孫琦則進一步推廣了上面的定理.

定理1.2[4]設(shè)f為形如(1)的多項式,其中Df＞0.若m≤n且Df在環(huán)Z/(q?1)Z 中左可逆,則對于任意的b∈Fq,有

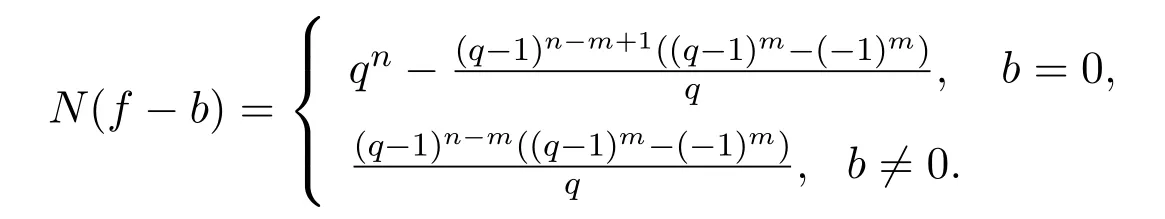
注意到“Df在環(huán)Z/(q?1)Z中左可逆”等價于“Df行等價于一個對角元素均為1的對角矩陣”,即.在文獻[5]中,王如允、聞彬彬和曹煒考慮了,其中λi∈{1,2}時的情形,得到了下面的結(jié)論.

定理 1.3[5]設(shè)f為形如 (1)的多項式,其中Df＞0,q=ph為奇數(shù).用η表示 F?q上的二次特征.設(shè)

且

(i)若p≡1(mod 4)或p≡3(mod 4)且h為偶數(shù)時,則有

(ii)若p≡3(mod 4)且h為奇數(shù)時,則有

2 預(yù)備知識

設(shè)g是的一個生成元.則對于,存在唯一的正整數(shù) 0≤t≤q?2,使得gt=a,記indga=t.定義上的Teichm¨uller特征χ滿足

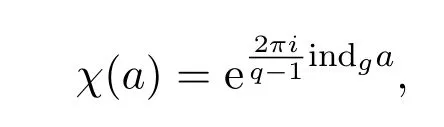
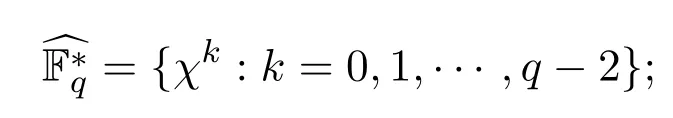
特別地,χk在中的階為(我們將在下面的引理 2.2和引理 2.3中用到這一事實).

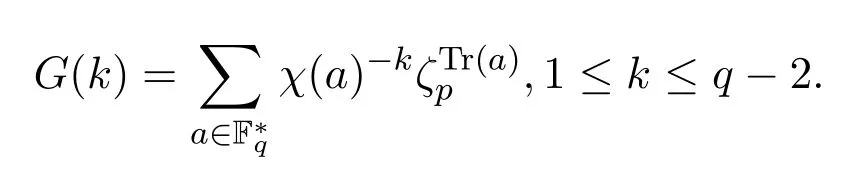
定義

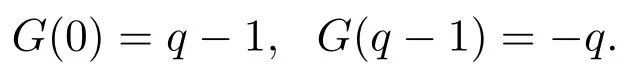
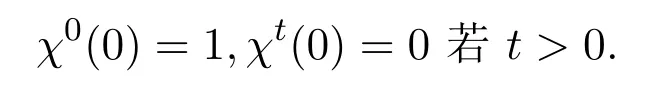
可以驗證,對于所有的a∈Fq,高斯和滿足下面的插值關(guān)系:

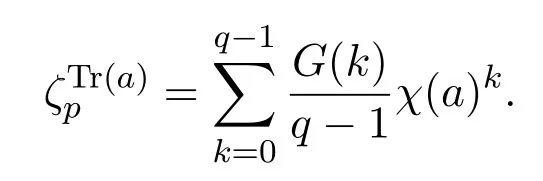
在下文中,固定

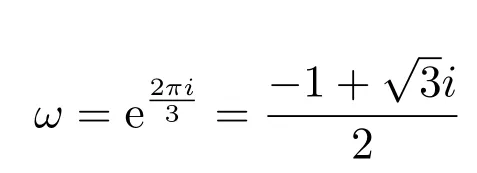
為C中的三次本原單位根,顯見ω2+ω+1=0.

定義 2.1[6]若q≡1(mod 3),則上的兩個三次特征分別為:

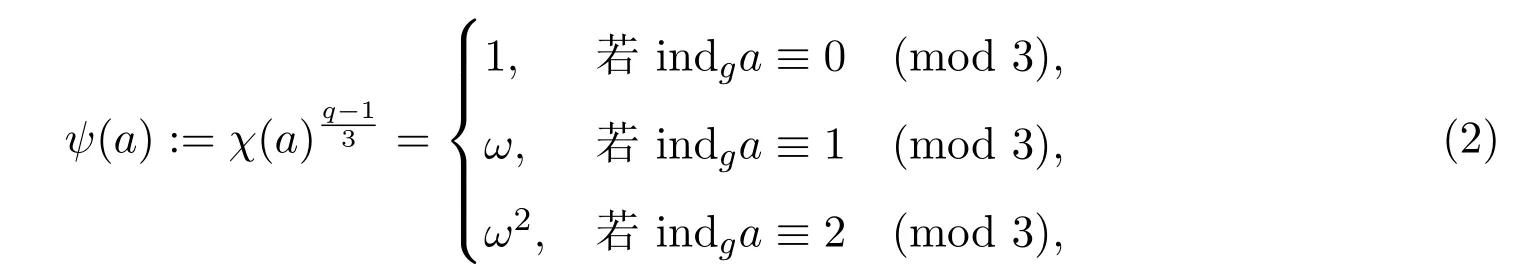
及

其相應(yīng)的高斯和分別為:

及

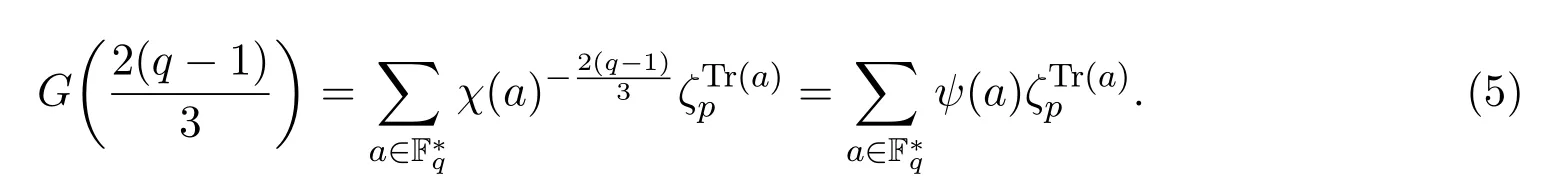
一般來講,高斯和是很難計算的,但(4)與(5)中高斯和的具體值在特殊情形下可以通過下面的引理得到.

引理 2.1[7]設(shè)p為素數(shù),M＞2是正整數(shù),存在一個最小的正整數(shù)u使得

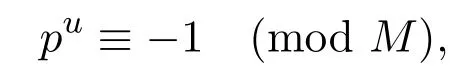
記q=p2uc,其中c為正整數(shù).若

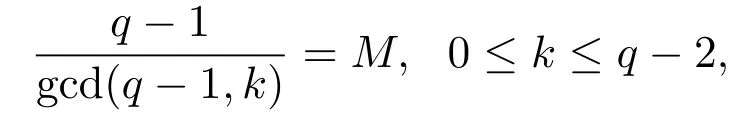
則有

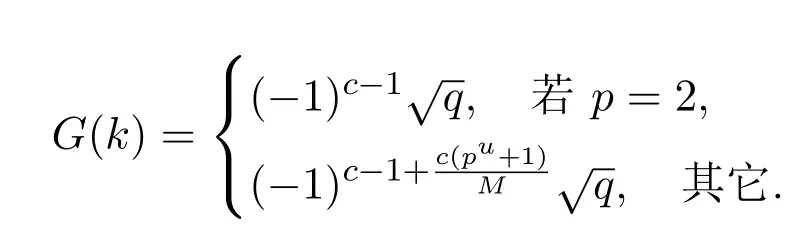
特別地,當(dāng)M=3時,我們有

引理 2.2設(shè)p為素數(shù),存在一個最小的正整數(shù)u使得pu≡?1(mod 3),記q=p2uc,其中c為正整數(shù).若或,則有

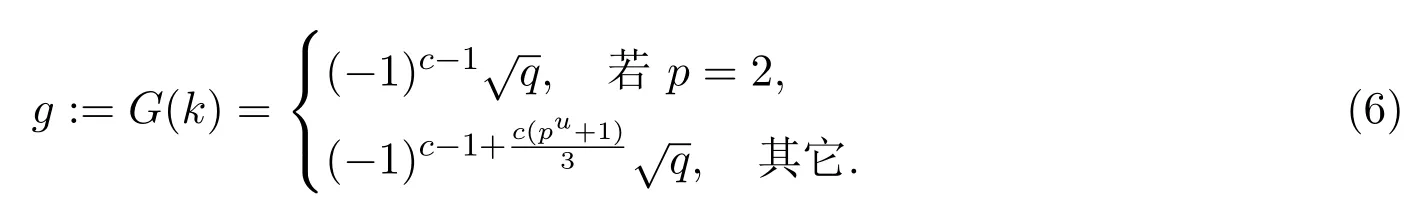
為方便計,在下文中我們總是用g表示(6)中G(k)的表達式.設(shè)f為形如(1)的多項式,其增廣矩陣為. 設(shè) ??{0,1,···,q?1},令

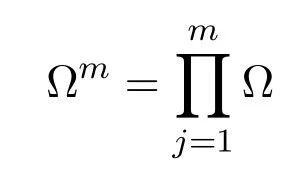
為 ? 的m重直積.對于向量k=(k1,···,km)∈?m,定義s(k)為向量中非零元素的個數(shù).沿用上述記號,有下面重要引理.

引理 2.3[8]設(shè)n元多項式f如 (1)中所示.令 ?={0,1,···,q?1},則有

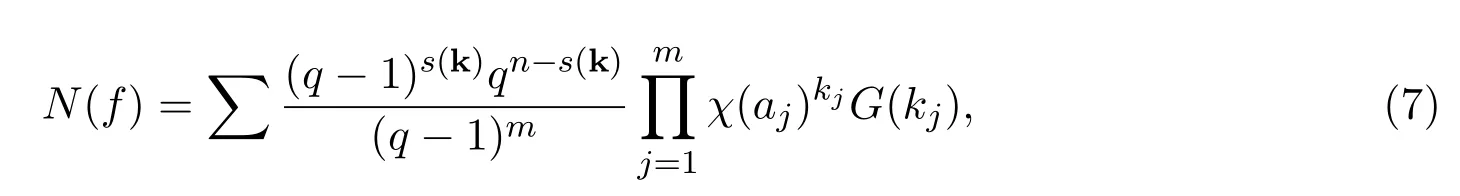
其中和號遍歷所有的向量k=(k1,···,km)∈?m且滿足

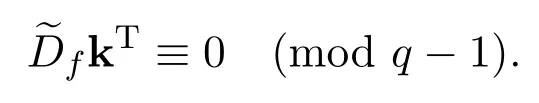
在下一節(jié)中,我們還會用到下面的組合恒等式(證明略).

引理 2.4設(shè)t為正整數(shù),則有

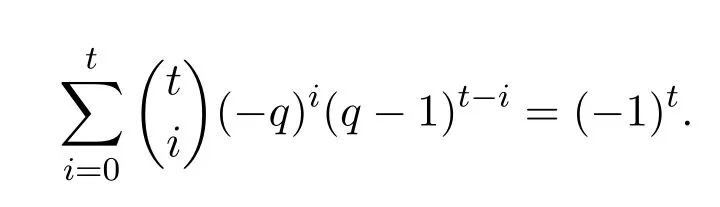
3 主要結(jié)論

為方便計,在本節(jié)中我們總是假定f是形如(1)定義的多項式,q=p2uc,且存在一個最小的正整數(shù)u使得

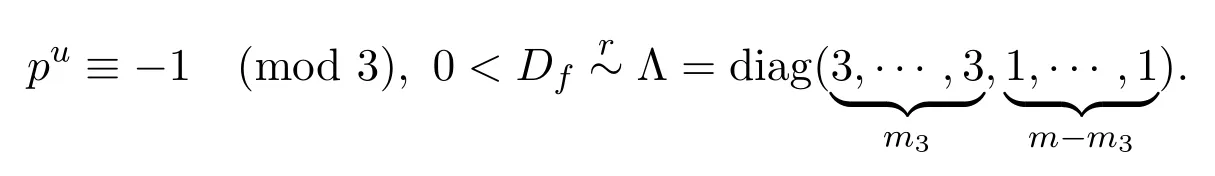
對系數(shù)集合

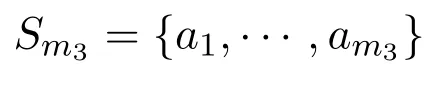
做如下劃分(0=m0≤m1≤m2≤m3≤m):

(a)t∈{1,2,···,m1}:ψ(at)=ω,k中所對應(yīng)的的元素記為k1=(k1,···,km1);

(b)t∈{m1+1,···,m2}:ψ(at)=ω2,k中所對應(yīng)的的元素記為k2=(km1+1,···,km2);

(c)t∈{m2+1,···,m3}:ψ(at)=ω3=1,k中所對應(yīng)的的元素記為k3=(km2+1,···,km3).對于給定的

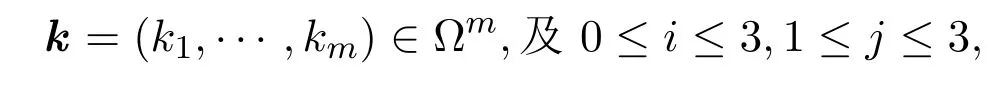
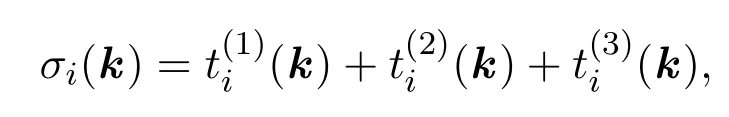
即在(k1,···,km3)中分量取值為i(q?1)/3 的個數(shù).

定理 3.1多項式f如本節(jié)前言所設(shè).令

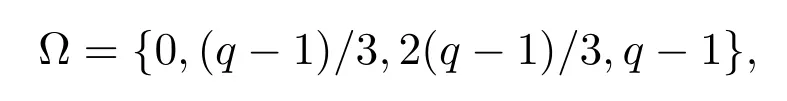
則有

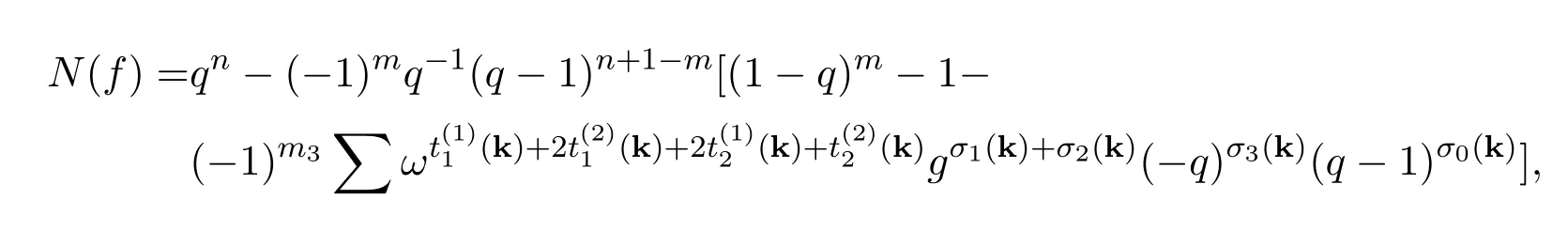
其中和號遍歷所有的向量k=(k1,···,km)∈?m且滿足:

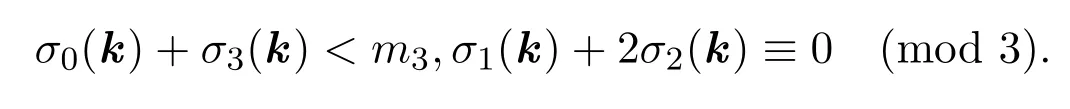
證明首先考慮

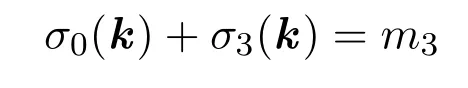
時的情形,并記此情形下的解數(shù)為N0.此時k=(k1,···,km)中向量取值只有q?1和0,即為定理1.2中b=0時的結(jié)論,故有

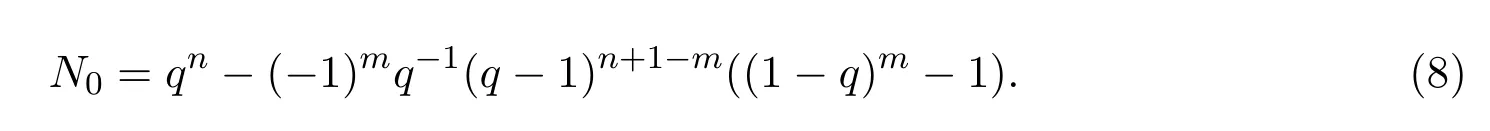
下面假設(shè)σ0(k)+σ3(k)＜m3,并記此情形下的解數(shù)為N?.由于

同余方程組

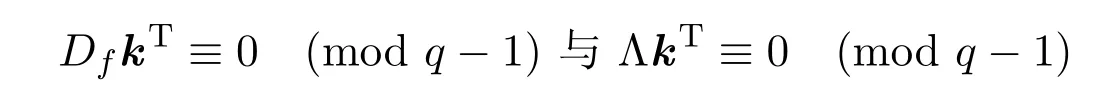
同解,且后者的解均取自于k=(k1,···,km)∈?m,這里

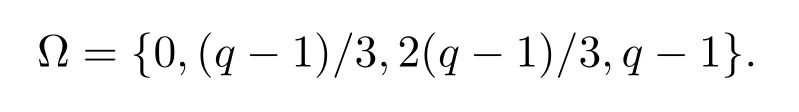
對任一給定的k=(k1,···,km)∈?m,由同余方程組的第一個方程可知,σ1(k)+2σ2(k)一定是3的倍數(shù).又因σ0(k)＜m3及Df＞0,故有s(k)=n+1.注意到當(dāng)k=0時,χ(aj)k=1,G(k)=q?1;當(dāng)k=q?1時,

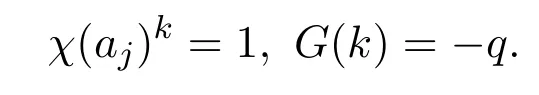
由(2),(3)及引理2.3,引理2.5可得

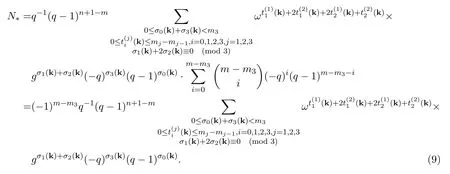
由N(f)=N0+N?,(8)和(9)立得結(jié)論.

當(dāng)系數(shù)集合Sm3中所有元素的三次特征均等于1（亦即均是中的立方數(shù)）時,我們可以得到較為簡潔的表達式.

推論 3.1設(shè)多項式f如本節(jié)前言所設(shè).令

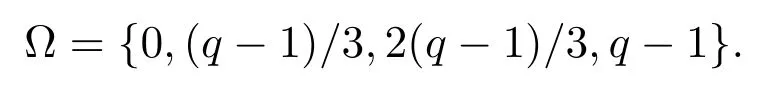
若m1=m2=0,則有

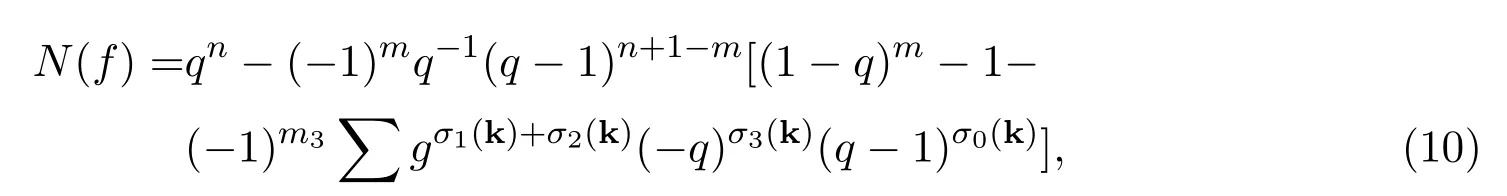
其中和號遍歷所有的向量k=(k1,···,km)∈?m且滿足

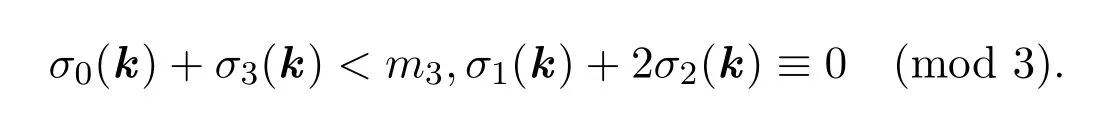
下面我們將給出N(f)的另一種表達式,它比定理3.1更適用于計算.

定理 3.2設(shè)多項式f如本節(jié)前言所設(shè),則有

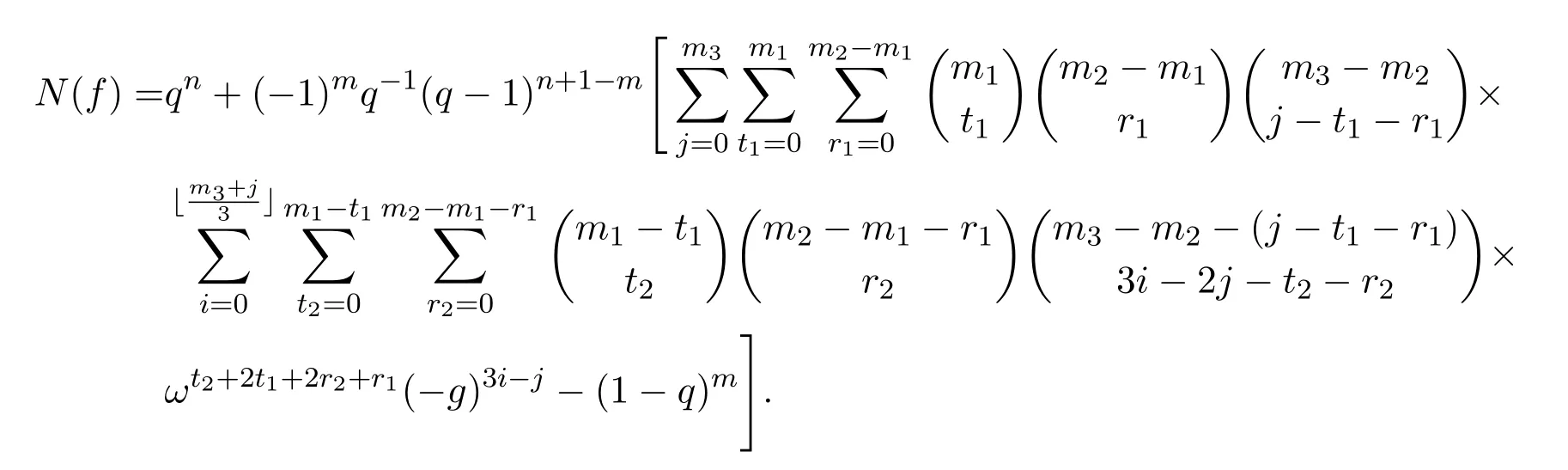
證明由本節(jié)前言假設(shè)知,系數(shù)集合Sm3={a1,···,am3}中有m1個三次特征為ω的元素,m2?m1個三次特征為ω2的元素,m3?m2個三次剩余特征為1的元素.由同余方程組

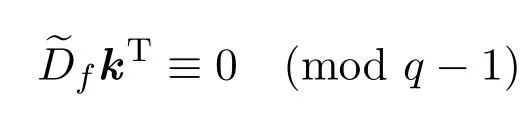
的第一個方程可得,

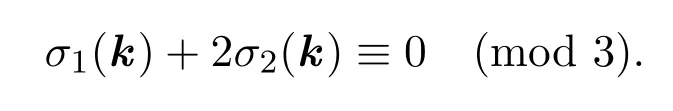
對于每個

從k1中取t1個元素,從k2中取r1個元素,從k3中取σ1(k)?t1?r1個元素,因此共有

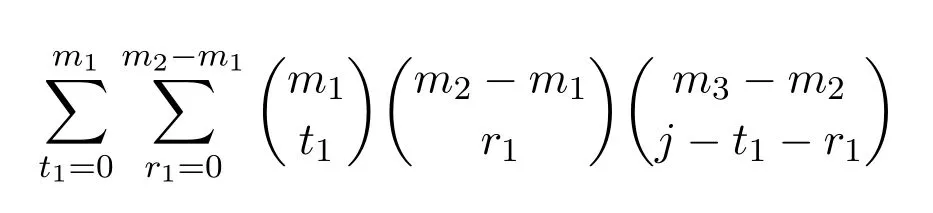
種取法.由于

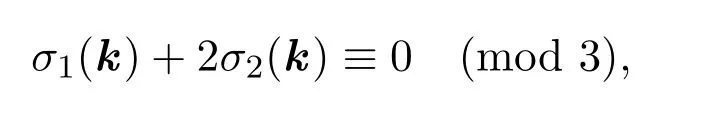
不妨假設(shè)

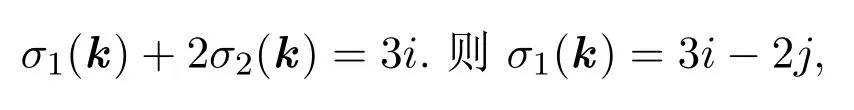
故有

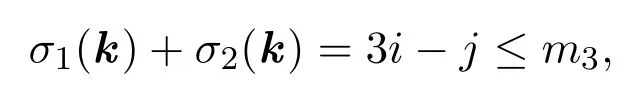
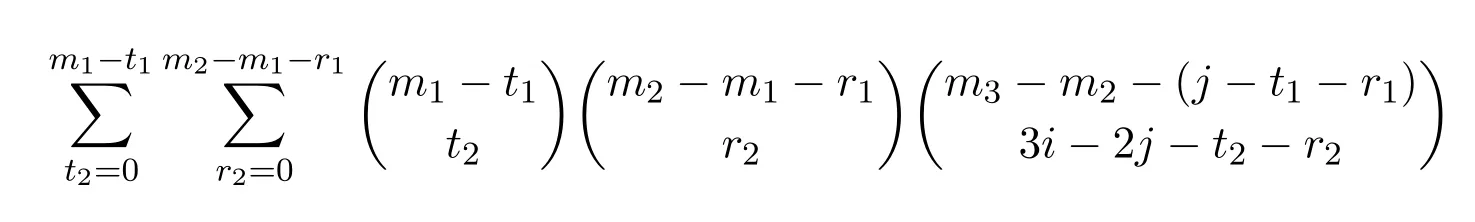
種取法.注意到,當(dāng)σ1(k)+σ2(k)＞0時,均有s(k)=n+1;而當(dāng)σ1(k)+σ2(k)=0,即i=j=0時,s(k)≤n+1,因而在求和中必須把這種情形排除掉.但

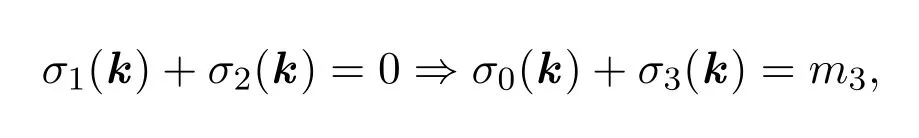
此種情形已在定理 3.1的證明中討論過,其公式即為定理 1.2中b=0時的公式,我們?nèi)杂肗0來表示.綜上討論,有

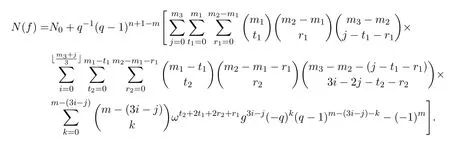
應(yīng)用引理2.4并進一步化簡,即得結(jié)論.

類似推論3.1,當(dāng)系數(shù)集合Sm3中所有元素的三次特征均等于1時,有

推論 3.2設(shè)多項式f如本節(jié)前言所設(shè).若m1=m2=0,則有

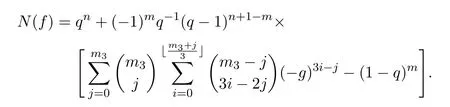
最后我們用一個具體的例子來說明如何分別應(yīng)用定理3.1和定理3.2.

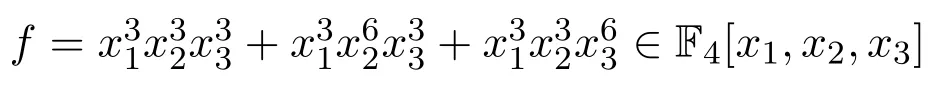
解顯然,m1=m2=0,m3=n=m=3,f的次數(shù)矩陣

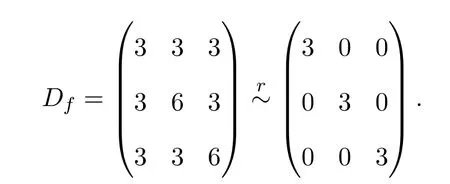
因此可應(yīng)用推論3.1和推論3.2.又由引理2.2知,此時g=2.

方法一:令?={0,1,2,3}.首先將所有滿足

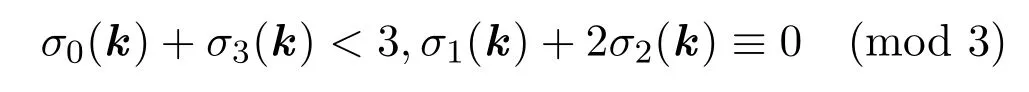
的向量k=(k1,k2,k3)∈?3列表 (見表1).

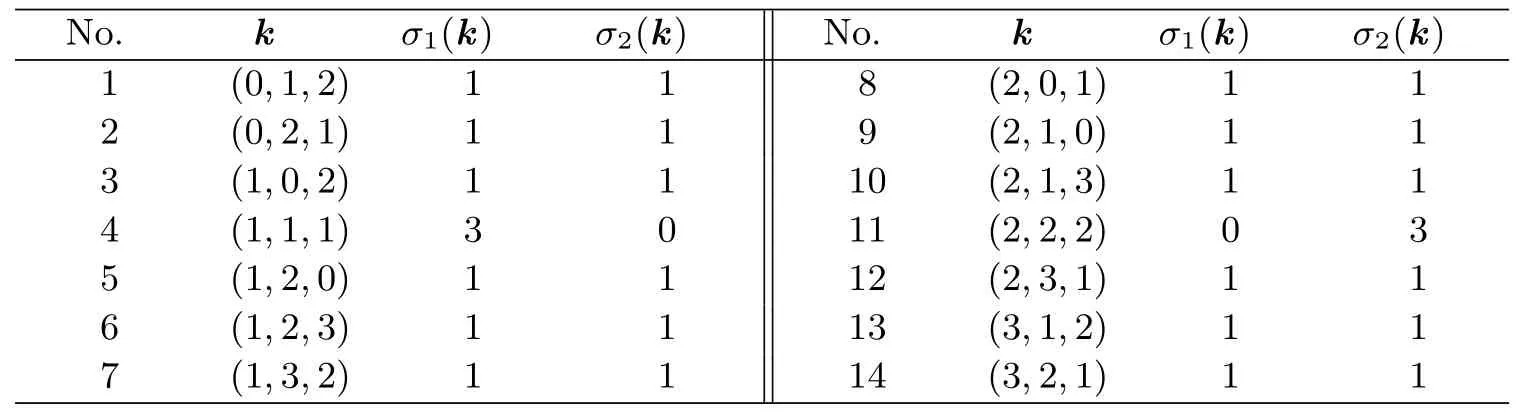
表1 向量k=(k1,k2,k3)∈?3的取值

再將上述結(jié)果代入推論3.1中的公式(10),計算可得N(f)=37.

方法二(應(yīng)用推論3.2):直接代入推論3.2中公式,有

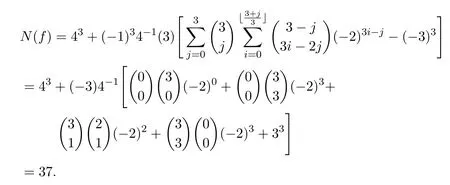
此外,通過Maple計算,亦可驗證N(f)=37.

[1]馮克勤,廖群英.有限域及其應(yīng)用[M].大連:大連理工大學(xué)出版社,2011.

[2]Lidl R,Niederreiter H.Finite Fields[M].Cambridge UK:Cambridge Univ.Press,1997.

[3]Sun Q.The Formula for the number of solutions of a class of equations over a fi nite fi eld[J].Chinese Ann.Math.Ser.A.,1997,18:403-408.

[4]Cao W,Sun Q.On a class of equations with special degrees over fi nite fi elds[J].Acta Arith.,2007,130:195-202.

[5]Wang R Y,Wen B B,Cao W.Degree matrices and enumeration of rational points of some hypersurfaces over fi nite fi elds[J].Journal of Number Theory,2017,177:92-99.

[6]Ireland K,Rosen M.A Classical Introduction to Modern Number Theory[M].New York:Springer-Verlag,1982.

[7]Cao X W,Chou W S.On the number of solutions of certain diagonal equations over fi nite fi elds[J].Finite Fields Appl.,2016,42:225-252.

[8]Cao W.Smith normal form of augmented degree matrix and its applications[J].Linear Algebra Appl.,2009,431:1778-1784.

Gauss sums and computation of rational points in fi nite fi elds

Wang Xiuzhi,Wang Ruyun,Cao Wei
(Department of Mathematics,Ningbo University,Ningbo 315211,China)

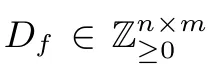
fi nite fi eld,rational point,character sum,Gauss sum

2010 MSC:11M06

O156

A

1008-5513(2017)06-0634-10

10.3969/j.issn.1008-5513.2017.06.009

2017-11-05.

國家自然科學(xué)基金(11371208);寧波市自然科學(xué)基金(2017A610134).

王秀芝(1993-),碩士生,研究方向：數(shù)論、有限域及其應(yīng)用.