阿力木·米吉提

(新疆廣播電視大學遠程教育學院,新疆烏魯木齊830049)

一個供應鏈系統(tǒng)可靠性模型時間依賴解的漸近行為

阿力木·米吉提

(新疆廣播電視大學遠程教育學院,新疆烏魯木齊830049)

本文研究一個供應鏈系統(tǒng)可靠性模型的時間依賴解.利用C0-半群理論研究該模型相應算子的譜的特征,獲得了該系統(tǒng)模型時間依賴解的漸近行為,推廣了文獻[8]中的結果.

供應鏈系統(tǒng);特征值;豫解集;幾何重數

1 引言

在全球化趨勢下,對于供應鏈這個日益復雜的系統(tǒng),如何分析和提高其可靠性變得日益迫切,并受到越來越多的關注[1-6,8].Thomas于2002年首次將可靠性工程應用到供應鏈中,提出用可靠度來度量供應鏈系統(tǒng)的可靠性[3].Sohn等認為供應鏈的可靠性就是顧客要求的產品質量可靠性[4].王建、張文杰從單級供應鏈可靠性分析出發(fā)進行了可靠性的定量分析,并根據分析結果提出了一些提高供應鏈可靠性的措施[5].在文獻[6]中作者通過分析供應鏈系統(tǒng)的狀態(tài)之間的轉移關系,引入補充變量,用補充變量法[7],建立了供應鏈系統(tǒng)的可靠性模型,并對該模型系統(tǒng)解的存在唯一性進行討論和證明.在文獻[8]中當修復率為常數時討論系統(tǒng)解的漸近性質.本文在文獻[6]的基礎上當修復率為函數時,通過研究相應算子的譜的特征得到該系統(tǒng)時間依賴解的漸近行為.

2 供應鏈系統(tǒng)模型的轉換

由文獻[6]知道,該供應鏈系統(tǒng)的數學模型用以下方程組描述:

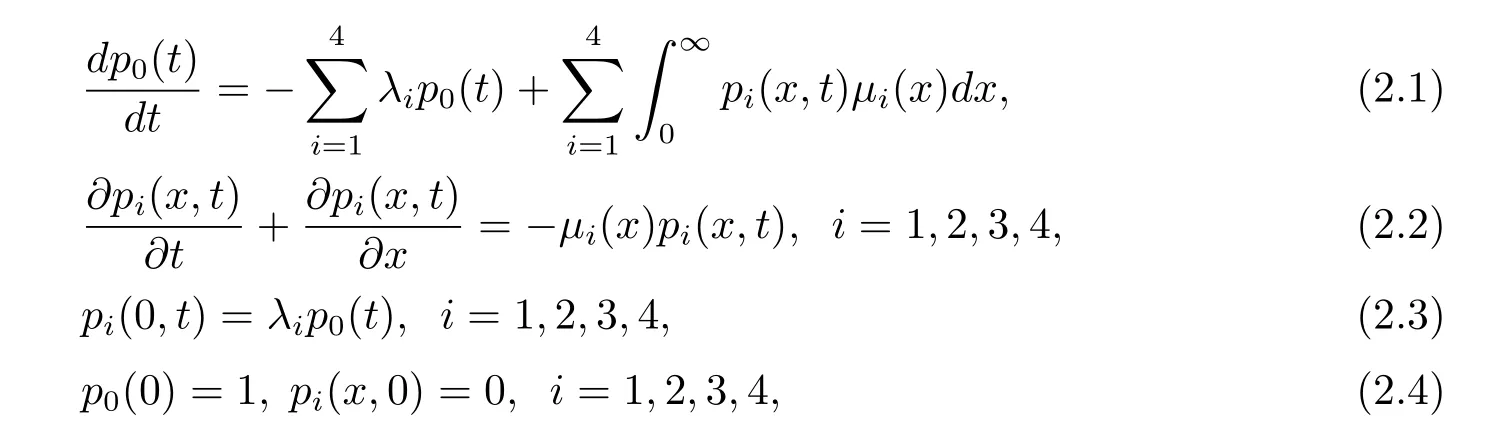
其中(x,t)∈[0,∞)×[0,∞);p0(t)表示在時刻t供應鏈系統(tǒng)正常運作的概率;pi(x,t)dx(i=1,2,3,4)表示在時刻t供應鏈系統(tǒng)處于故障狀態(tài)i(i=1,2,3,4),在該狀態(tài)已經駐留了x時間,在(x,x+dx]離開故障狀態(tài)的概率;λi(i=1,2,3,4)是從正常運作狀態(tài)到狀態(tài)i(i=1,2,3,4)的失效率;μi(x)(i=1,2,3,4)表示供應鏈系統(tǒng)離開狀態(tài)i(i=1,2,3,4)的修復率.

取狀態(tài)空間為

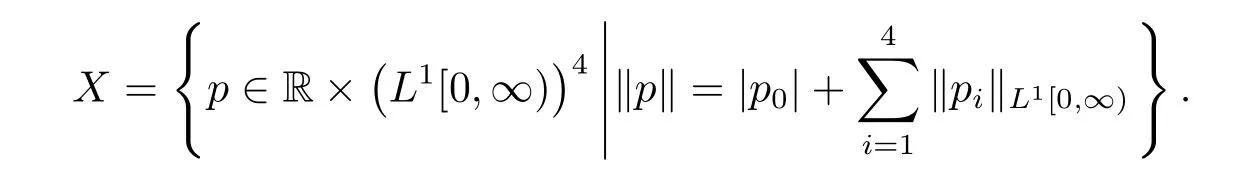
顯然,X是一個Banach空間[9].為簡單起見,定義

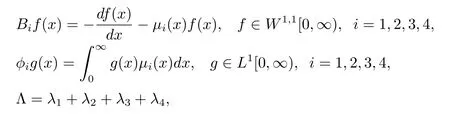
則可以定義算子Am和它的定義域D(Am)為

選取X的邊界空間?X:=C4,并且定義邊界算子L:D(Am)→?X與Φ:D(Am)→?X如下:

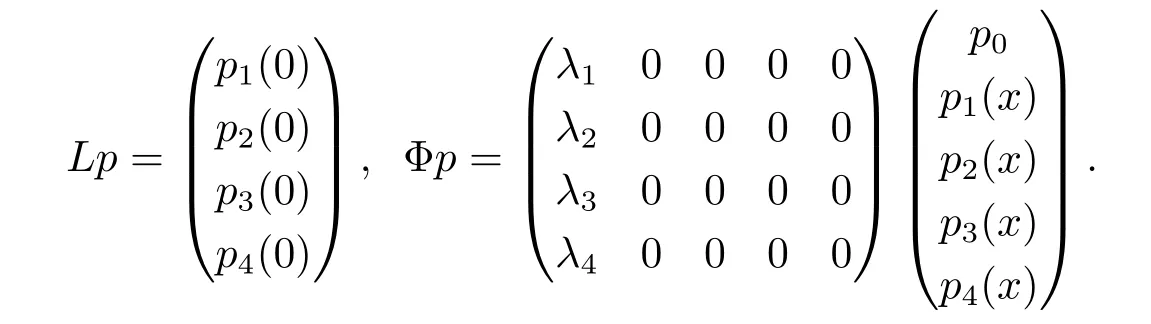
如果定義算子(A,D(A))為Ap=Amp,D(A)={p∈D(Am)|Lp=Φp},那么方程(2.1)–(2.4)可以描述為Banach空間X上的抽象Cauchy問題:

在文獻[6]中作者得到了以下結果.

定理2.1算子(A,D(A))生成一個正壓縮C0-半群T(t).系統(tǒng)(2.5)存在唯一的正時間依賴解p(x,t)=T(t)p(0),并且滿足

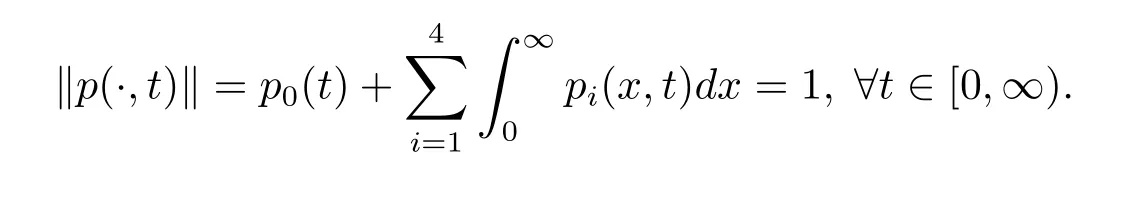
3 系統(tǒng)(2.5)相應算子的譜特征

引理3.10是A的幾何重數為1的特征值.

證討論方程Ap=0,即

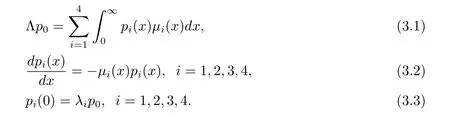
解(3.2)有

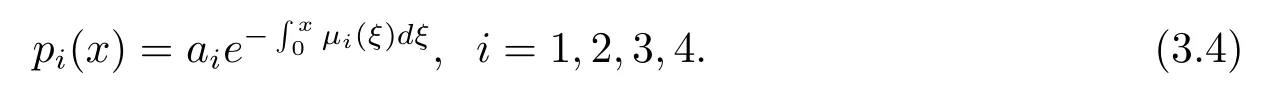
(3.4)式結合(3.3)式推出

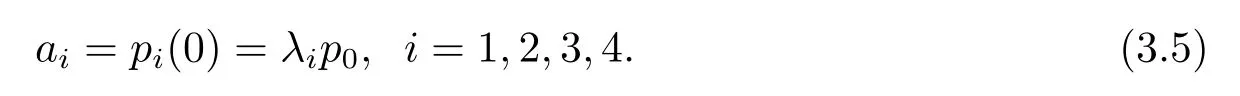
由(3.4)與(3.5)式算出

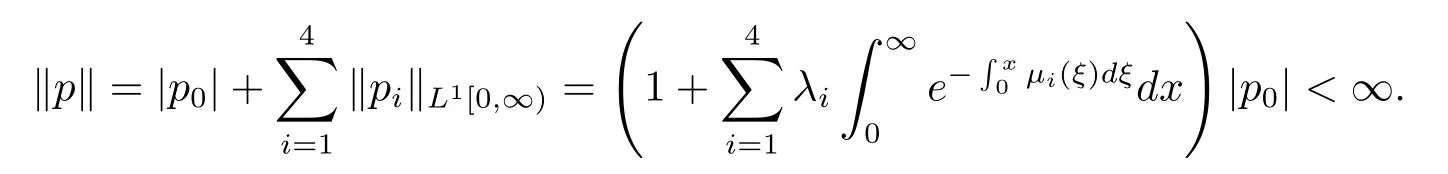
這說明0是A的特征值.由(3.1),(3.4),(3.5)式知道對應于0的特征向量空間是一維的線性空間,即0的幾何重數為1.證畢.

下面研究A的豫解集.為此首先定義算子(A0,D(A0))并研究它的豫解集;其次通過考慮(γI-Am)的核來定義Dirichlet算子Dγ并推出ΦDγ的表達式;然后用文獻[10]中的結果得到A的豫解集,從而推出本文的主要結果.

定義算子(A0,D(A0))為

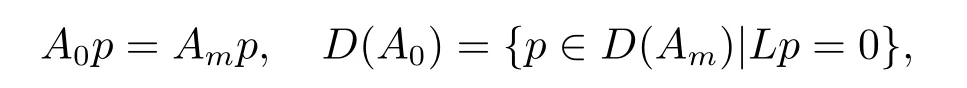
那么對任意y∈X,考慮方程(γI-A0)p=y,這等價于

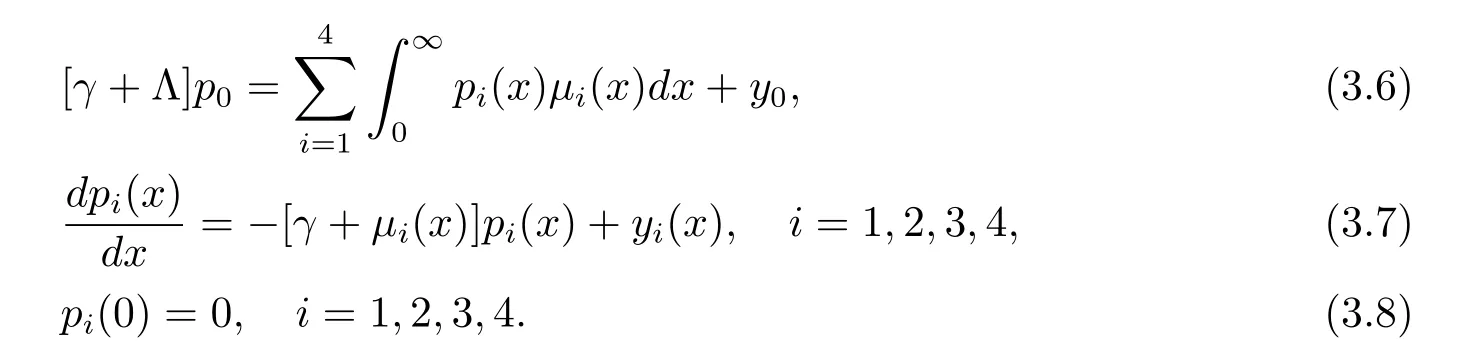
解(3.6)與(3.7)推出

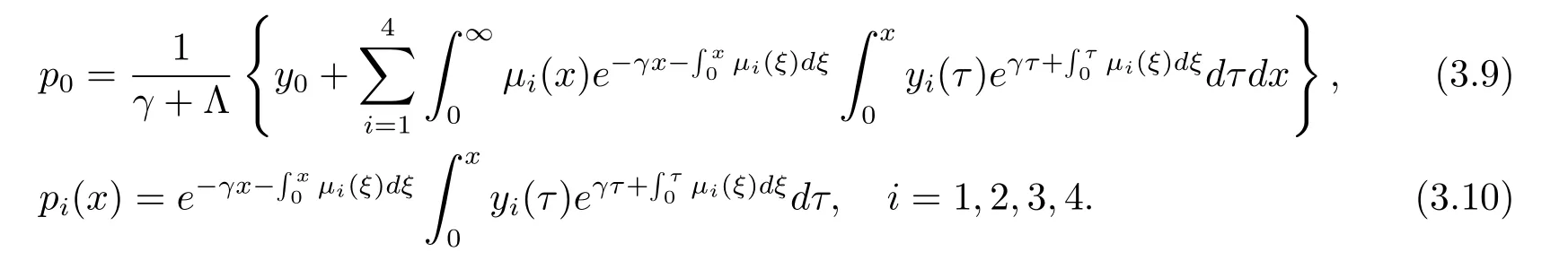
?f∈L1[0,∞),若記

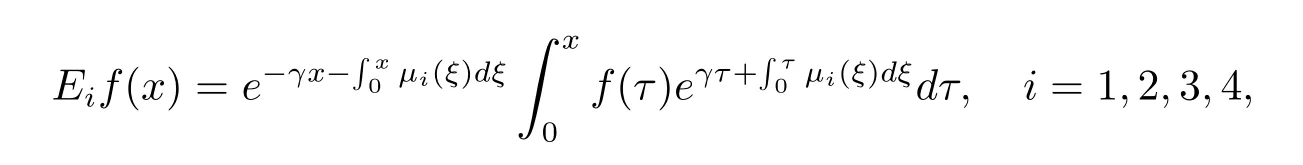
那么(3.9)與(3.10)式變?yōu)?/p>

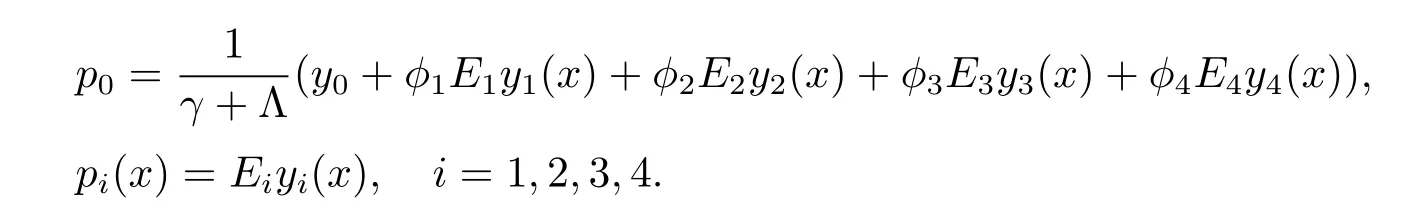
即

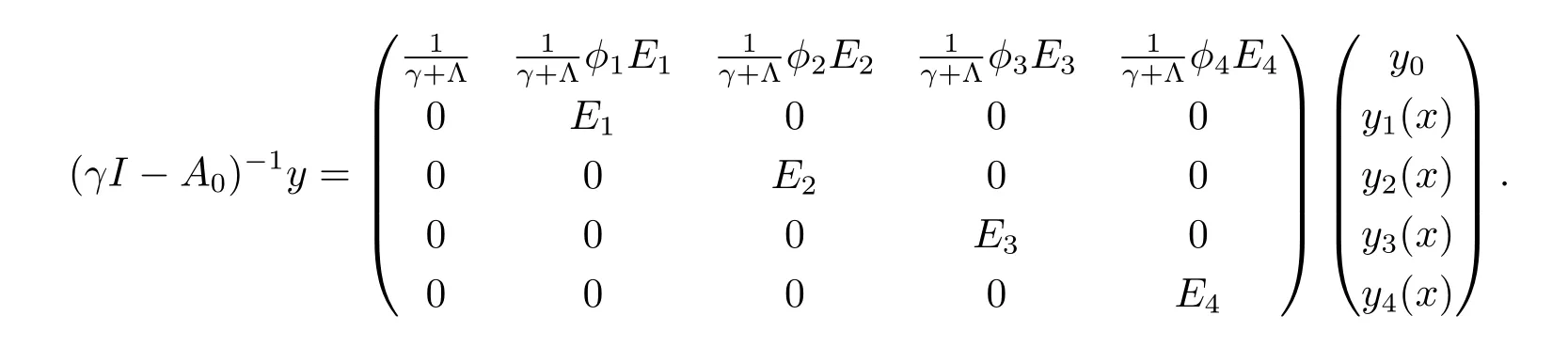
由上述表達式和豫解集的定義可得以下結論.

引理3.2設μi(x):[0,∞)→[0,∞)(i=1,2,3,4)是可測函數,若

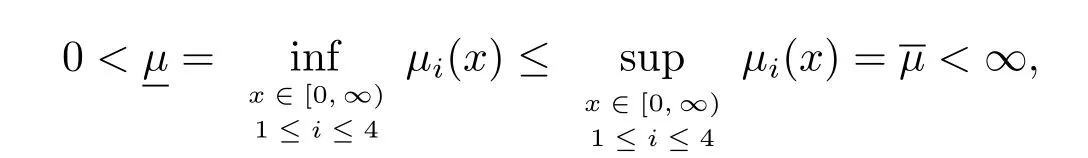
證對任意的f∈L1[0,∞)用分部積分法估計出

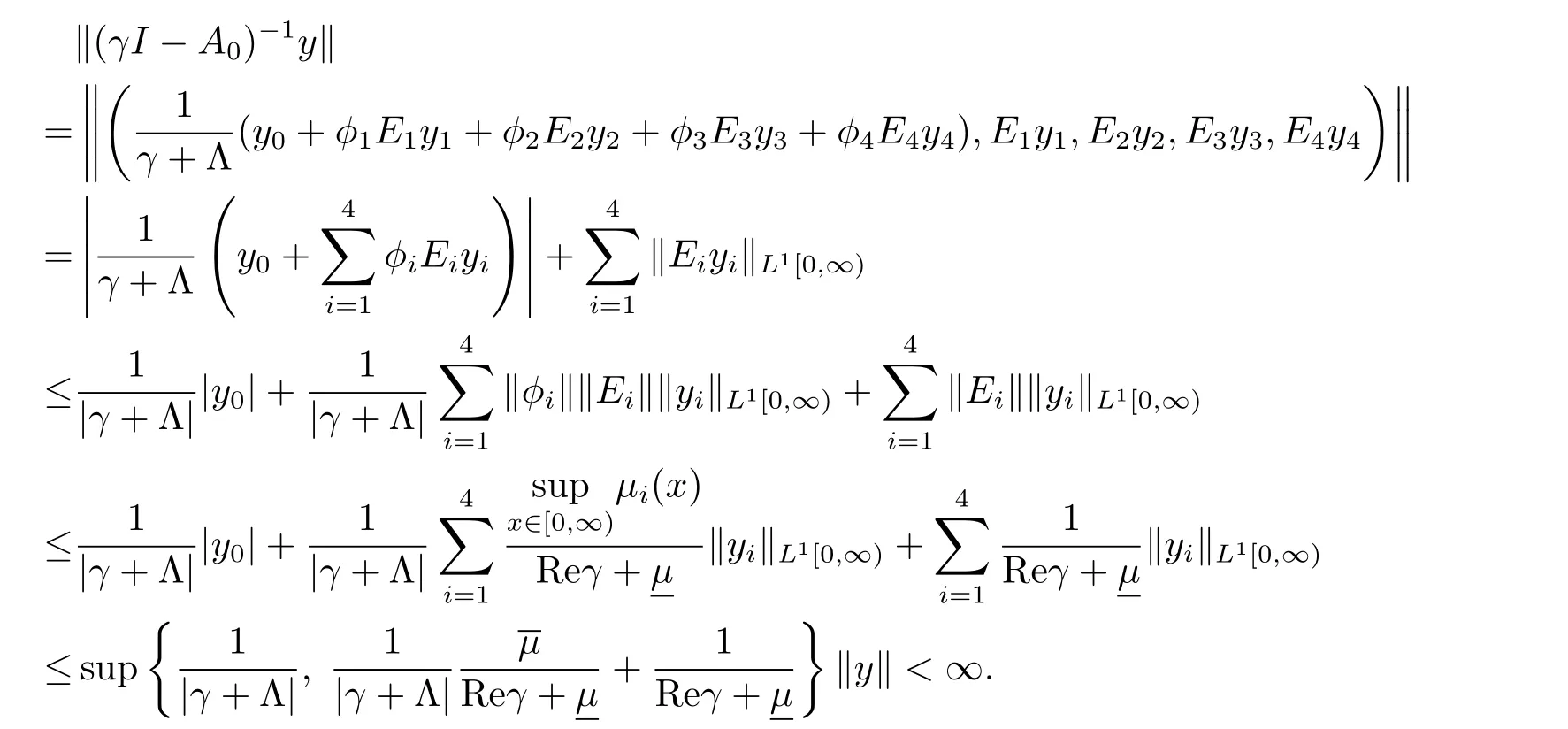
此式說明引理的結論成立.證畢.

引理3.3設μi(x)(i=1,2,3,4)是可測函數,且

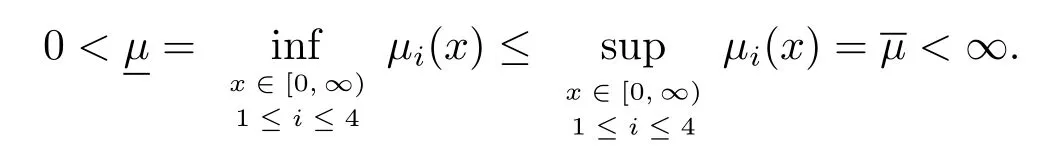
若γ∈ρ(A0),則

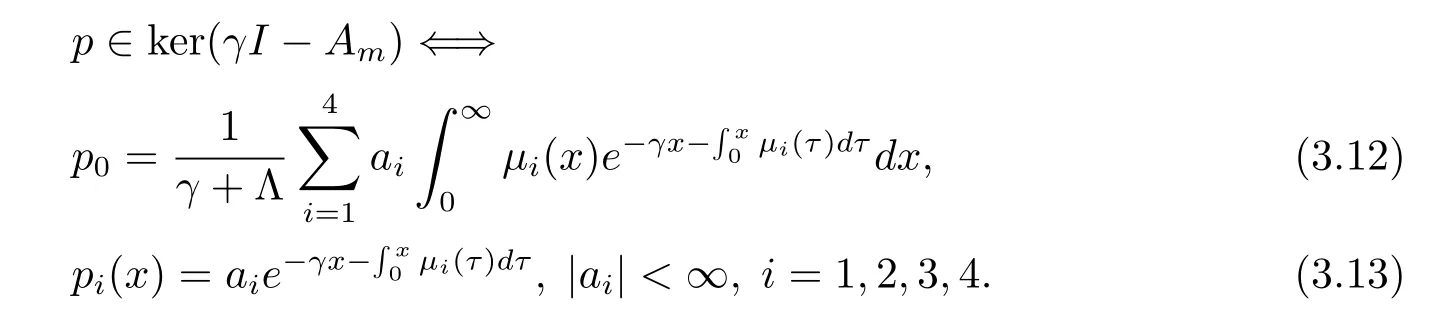
證如果p∈ker(γI-Am),則(γI-Am)p=0,這等價于

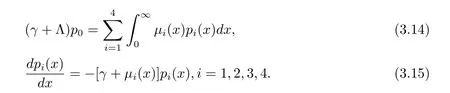
解(3.15)推出

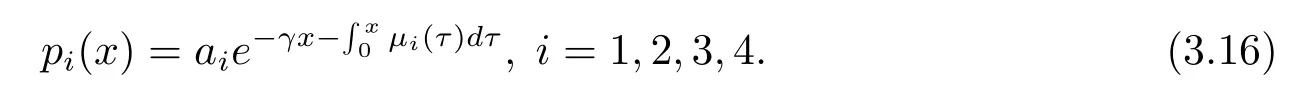
將(3.16)式代入(3.14)式算出

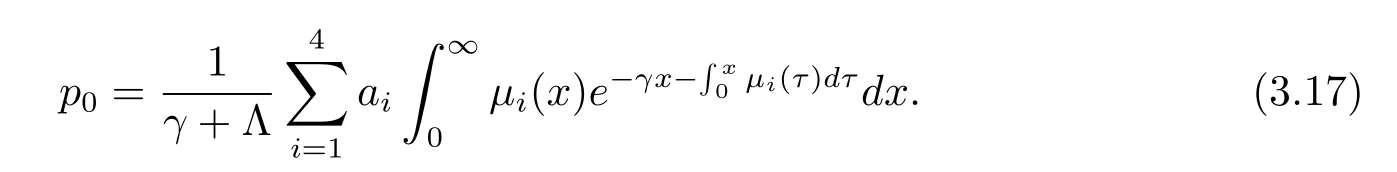
由于p∈ker(γI-Am),p∈D(Am),所以用嵌入定理[11]得到

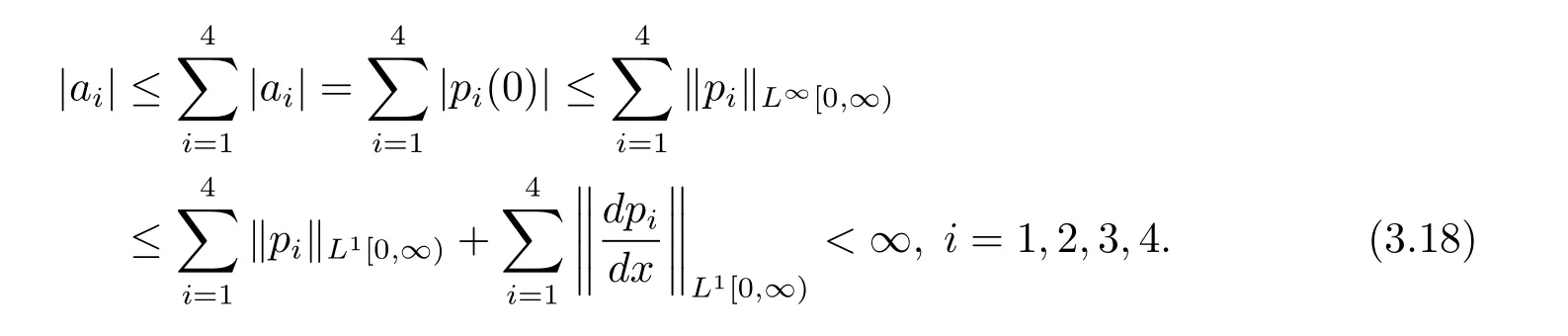
(3.16)–(3.18)式說明(3.12)與(3.13)式成立.

反之,如果(3.12),(3.13)式成立,則有

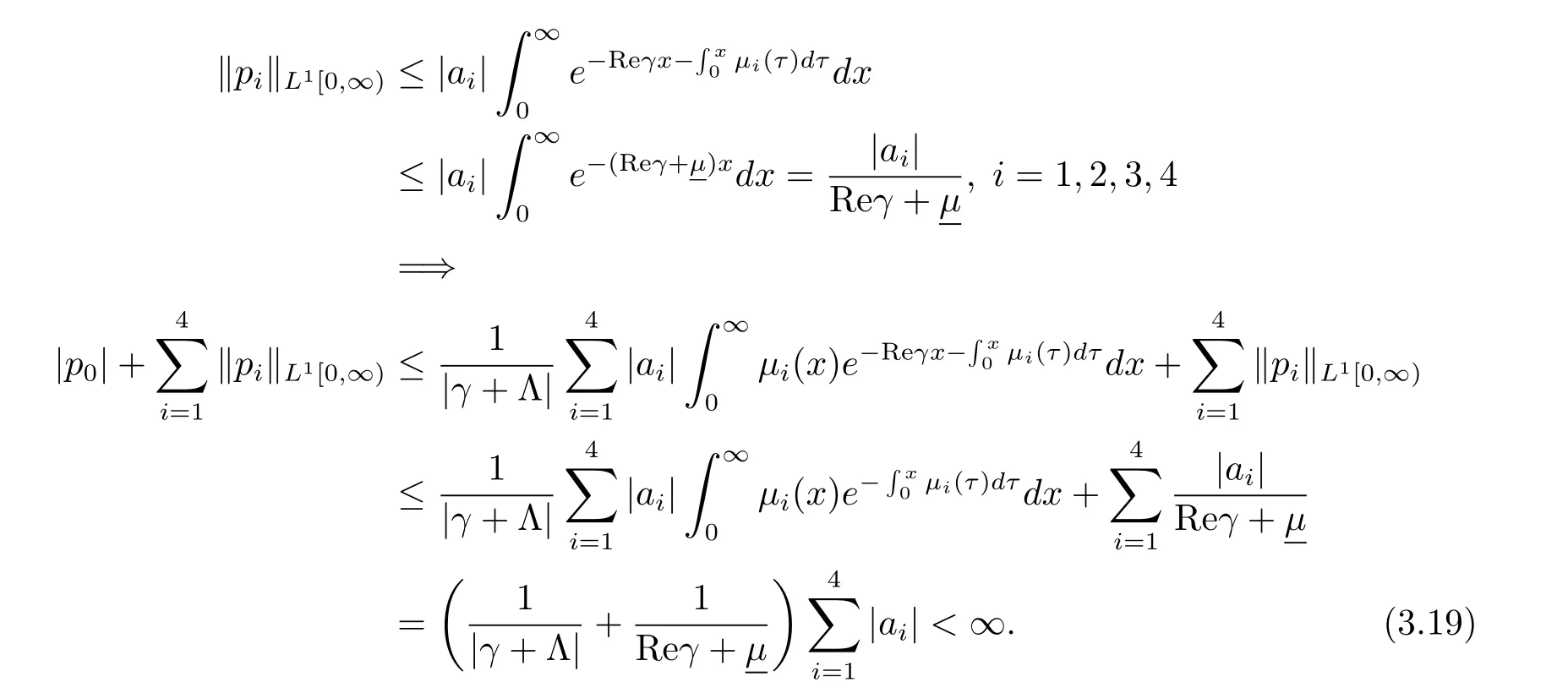
由(3.13)式知道

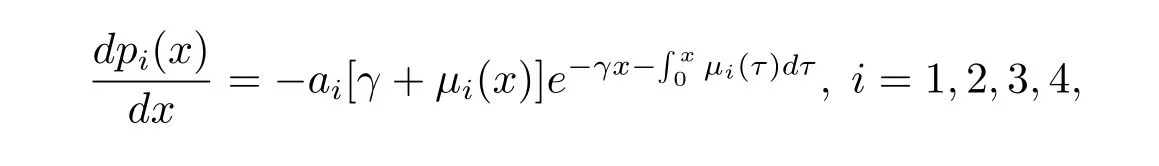
從而有

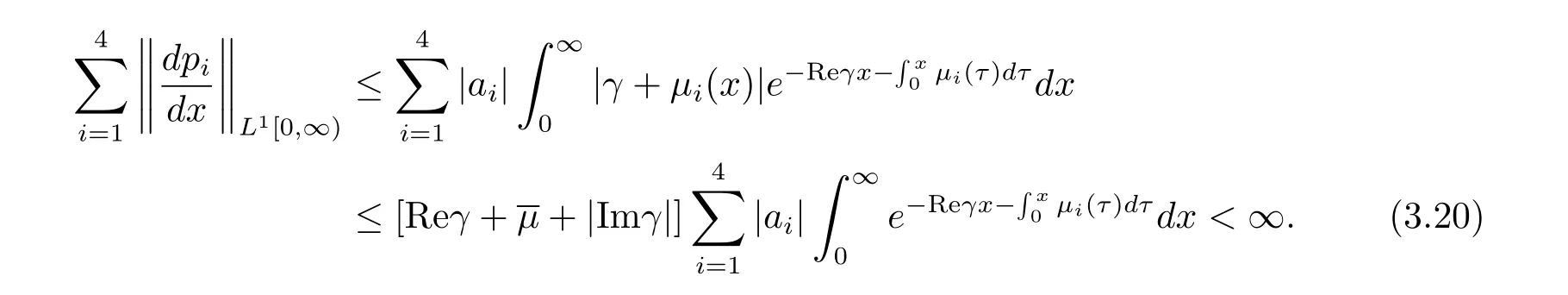
(3.19)與(3.20)式表示p∈ker(γI-Am).證畢.

由于L是滿射,所以

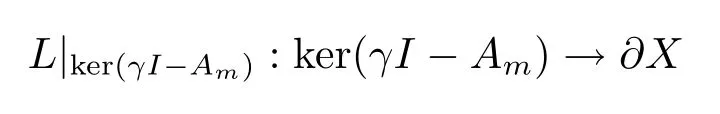
可逆.如果γ∈ρ(A0),那么定義Dirichlet算子為

由引理3.3知道Dγ的具體表達式為

其中αi=i=1,2,3,4.

由Dγ的表達式和Φ的定義推出ΦDγ的表達式

這里εij=dx,i,j=1,2,3,4.

在文獻[10]中作者得到以下結果.

引理3.4設γ∈ρ(A0)且存在γ0∈C使得則

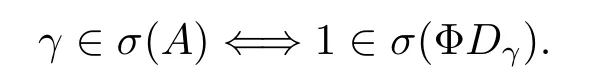
結合引理3.4與文獻[12]得到如下結論:

引理3.5設μi(x)(i=1,2,3,4)是可測函數,若

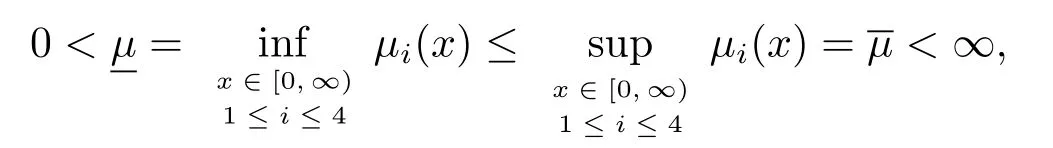
那么在虛軸上除了0外其他所有點都屬于A的豫解集.

證設＜∞(k=1,2,3,4),并且γ=ih,h∈R{0}.由 Riemann-Lebesgue引理

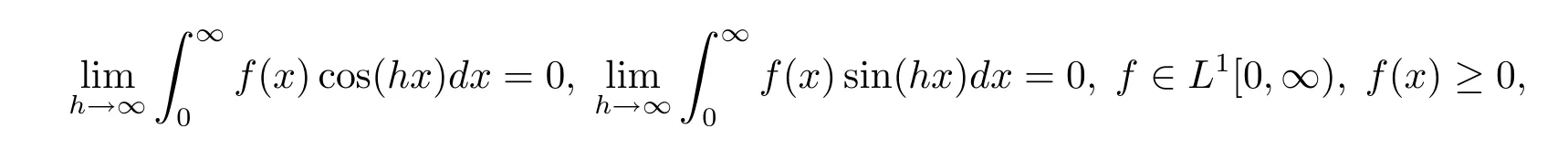
知道存在非負常數K＞0使得對一切|h|＞K有

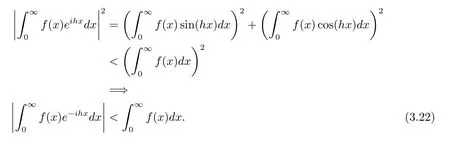
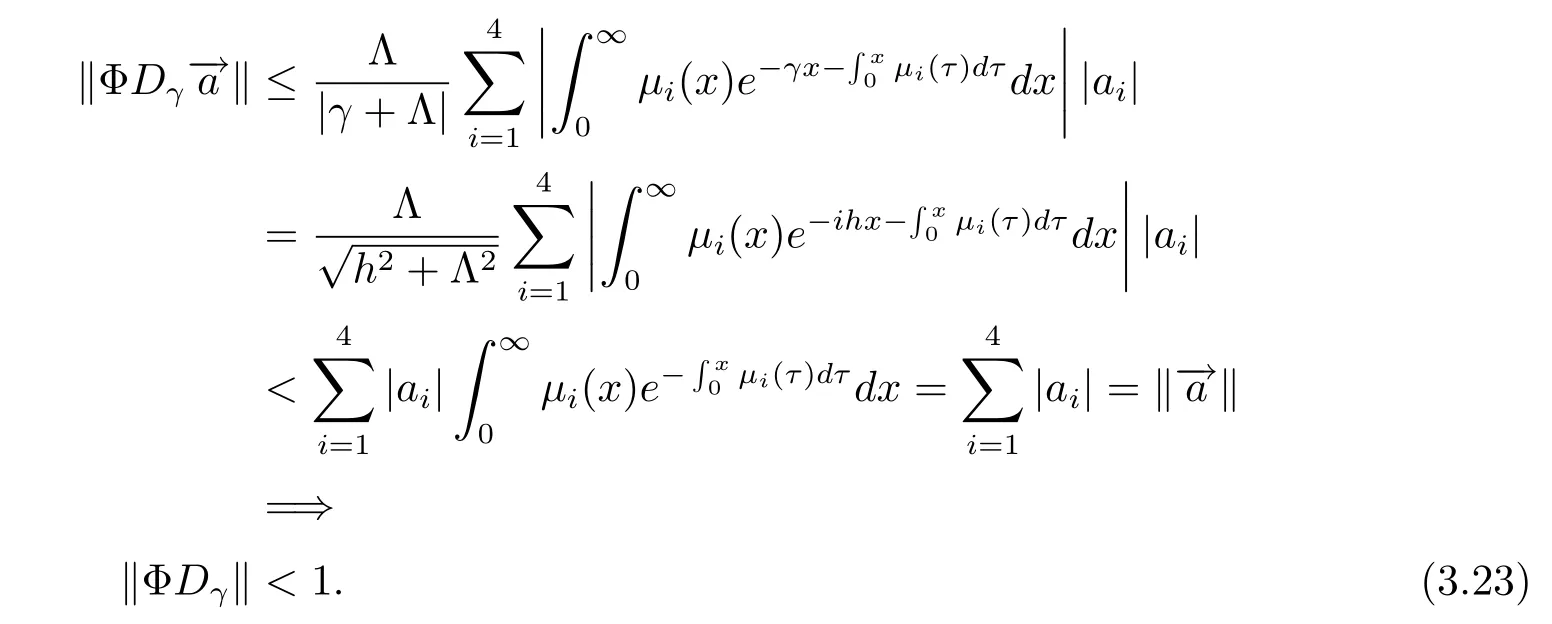
(3.23)式表明當|h|＞K時譜半徑r(ΦDγ)＜‖ΦDγ‖＜1,這說明1此結果結合引理3.4知道當|h|＞K時有即

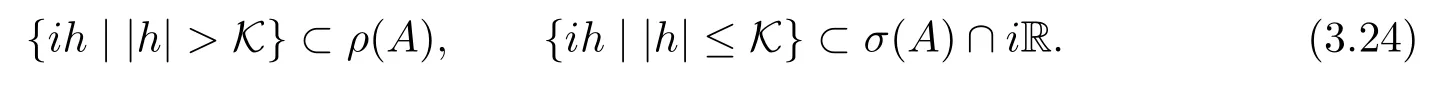
另外由定理2.1與文獻[12]中的推論2.3知道σ(A)∩iR是虛加法循環(huán).即

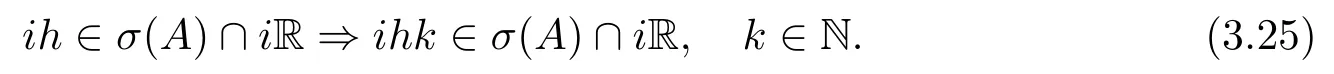
從而由(3.24),(3.25)式與引理3.1推出σ(A)∩iR={0}.證畢.

由文獻[13]知道X的共軛空間為

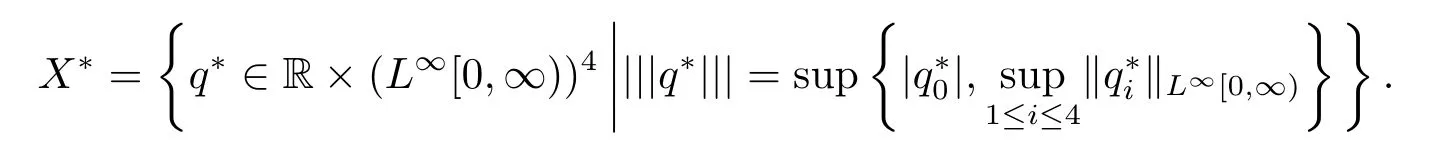
容易證明X?是一個Banach空間[7].根據文獻[8]知道A的共軛算子A?為

其中

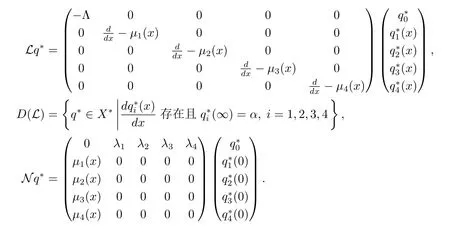
下面證明0是A?的幾何重數為1的特征值.

引理3.60是A?的幾何重數為1的特征值.

證考慮方程A?q?=0,即

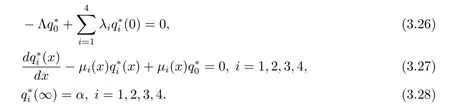
解(3.27)有

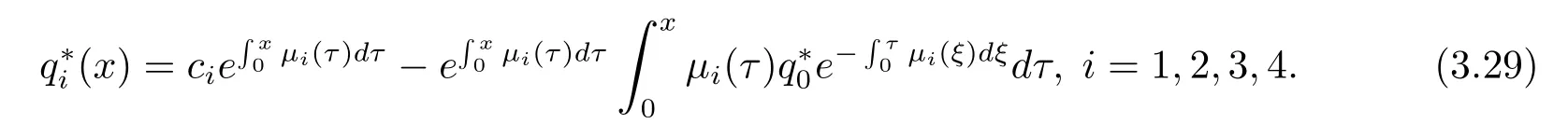
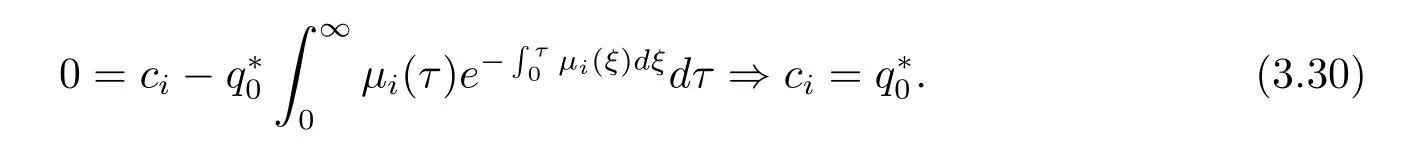
(3.30)式代入(3.29)式可得

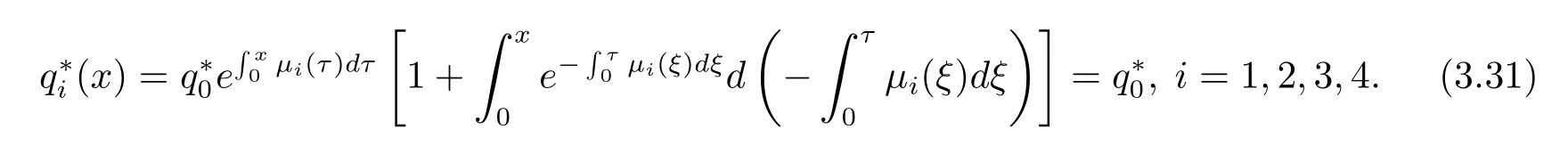
(3.31)式表明

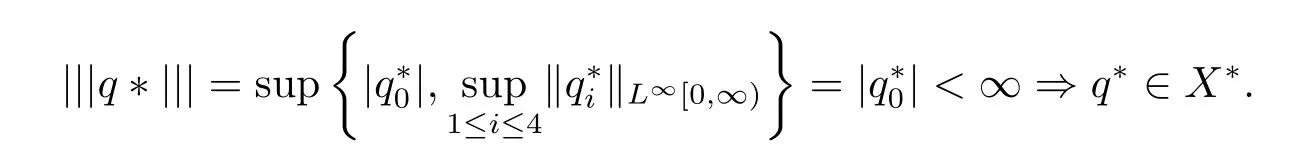
即0是A?的特征值.由(3.31)式看出對應于0的特征向量空間是1維的.換句話說,0的幾何重數為1.證畢.

4 系統(tǒng)(2.5)時間依賴解的漸近行為

結合定理2.1,引理3.1,引理3.5,引理3.6與文獻[14]中的定理14推出本文的主要結論.

定理4.1設μi(x)(i=1,2,3,4)是可測函數,且滿足

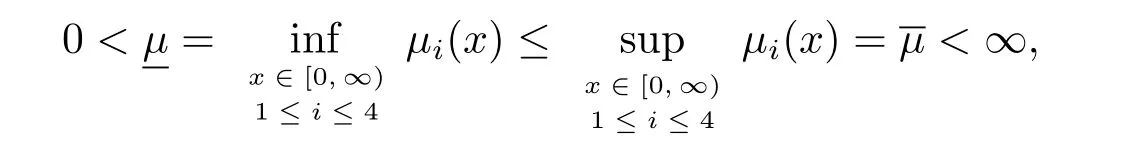
則系統(tǒng)(2.5)的時間依賴解強收斂于該系統(tǒng)的穩(wěn)態(tài)解,即

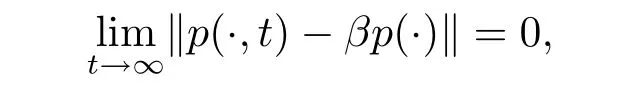
其中p(x)是引理3.1中的特征向量.

[1]周長禮,高成修,周偉剛,翟建壽.基于價格競爭的最優(yōu)定價策略與供應鏈的協(xié)調方法[J].數學雜志, 2010,30(4):682–688.

[2]陳榮軍,羿旭明,唐國春.自由作業(yè)環(huán)境下的供應鏈排序[J].數學雜志,2009,29(1):81–86.

[3]Thomas M U.Supply chain reliability for contingency operations[C].Rel.Maitain.Symp.,2002: 61–67.

[4]Shon S Y,Choi S.Fuzzy QFD for supply chain management with reliability consideration[J].Reliab. Eng.Syst.Saf.,2001,72(3):327–334.

[5]王建,張文杰.供應鏈系統(tǒng)可靠性分析[J].中國安全科學學報,2003,13(11):73–75.

[6]辛玉紅,鄭愛華,胡薇薇.一個供應鏈系統(tǒng)的可靠性模型的適定性分析[J].數學的實踐與認識,2008, 38(1):46–52.

[7]Gaver D P.Time to failure and availability of parallel redundant stystems with repair[J].IEEE Trans.Rel.,1963,12:30–38.

[8]邢喜民,王秀玲.一個供應鏈系統(tǒng)的可靠性模型的解的漸近性質[J].江南大學學報(自然科學版),2012, 11(1):108–112.

[9]阿力木·米吉提,蔡玲霞.第二種服務可選的M/M/1排隊模型狀態(tài)空間及對偶空間的完備性[J].新疆師范大學學報(自然科學版),2012,31(2):72–76.

[10]Haji A,Radl A.A semigroup approach to queueing systems[J].Semigroup Forum,2007,75(3): 609–623.

[11]Adams R A.Sobolev spaces[M].New York:Academic Press,1975.

[12]Nagel R.One-parameter semigroups of positive operators[M].Berlin:Springer-Verlag,1987.

[13]定光桂.巴拿赫空間引論(第二版)[M].北京:科學出版社,2008.

[14]Gupur Geni,Li Xuezhi,Zhu Guangtian.Functional analysis method in queueing theory[M].Hertfordshire:Res.Inform.Ltd.,2001.

ASYMPTOTIC BEHAVIOR OF THE TIME-DEPENDENT SOLUTION OF THE RELIABILITY MODEL FOR THE SUPPLY CHAIN

ALIM Mijit
(School of Distance Education,Xinjiang Radio&TV University,Urumqi 830049,China)

We study the time-dependent solution of the reliability model for the supply chain system.By using C0-semigroup theory we study the spectral properties of the underlying operator corresponding to the system model and obtain the asymptotic behavior of the time-dependent solution of the system,which extends the results in[8].

supply chain system;eigenvalue;resolvent set;geometric multiplicity

tion:47A10;47N20

O177.7

A

0255-7797(2017)01-0201-10

2014-04-23接收日期:2014-11-24

新疆少數民族科技人才特殊培養(yǎng)計劃科研項目資助(2016D0211).

阿力木·米吉提(1978–),男,維吾爾族,新疆阿克陶,副教授,主要研究方向:可靠性模型的動態(tài)分析.