CHEN Ya-li,SONG Wei-dong

(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China )

A CLASS OF DUALLY FLAT SPHERICALLY SYMMETRIC FINSLER METRICS

CHEN Ya-li,SONG Wei-dong

(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China )

This paper investigates the construction of dually flat Finsler metrics.By analysing the solution of the spherically symmetric dually flat equation,we construct new examples of dually flat Finsler metrics,obtain necessary and sufficient conditions of the solution to be dually flat.

dually flat;Finsler metric;spherically symmetric

1 Introduction

The notion of dually flat Riemannian metrics was initially introduced by Amari and Nagaoka[1]when they studied information geometry in 2000.A Finsler metric F=F(x,y) on an m-dimensional manifold M is called locally dually flat if at every point there is a coordinate system(xi)in which the spray coefficients are in the following form

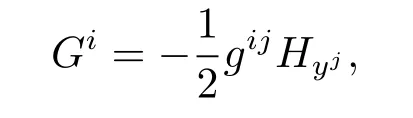
where H=H(x,y)is a local scalar function on the tangent bundle TM of M.Such a coordinate system is called an adapted coordinate system.Subsequently,without the quadratic restriction,the notion of dually flatness was extend to Finsler metrics by Shen when he studied Finsler information geometry[2].In[2],Shen proved that a Finsler metric F=F(x,y)on an open subset U?Rmis dually flat if and only if it satisfies the following equations

On the other hand,the study of spherically symmetric Finsler metrics attracted a lot of attention.Many known Finsler metrics are spherically symmetric[5–6,8].A Finsler metric F is said to be spherically symmetric(orthogonally invariant in an alternative terminology in[10])if F satisfies

for all A∈O(m),equivalently,if the orthogonal group O(m)acts as isometrics of F.Such metrics were first introduced by Rutz[11].

It was pointed out in[10]that a Finsler metric F on Bm(μ)is a spherically symmetric if and only if there is a function φ:[0,μ)×R→R such that

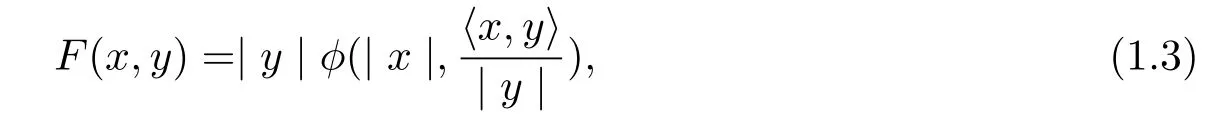
where(x,y)∈TRm(μ){0},|·|and〈·,·〉denote the standard Euclidean norm and inner product respectively.The spherically symmetric Finsler metric of form(1.3)can be rewritten as the following form[6]

Spherically symmetric Finsler metrics are the simplest and most important general (α,β)-metrics[12].Mo,Zhou and Zhu classified the projective spherically symmetric Finsler metrics with constant flag curvature in[13–15].A lot of spherically symmetric Finsler metrics with nice curvature properties was investigated by Mo,Huang et al.[10,13–16].

An important example of non-Riemmannian dually flat Finsler metrics is the Funk metric

on the unit ball Bm(μ),where y∈TxBm?Rm.Huang and Mo in[6]decomposed the Funk metric Θ in the form

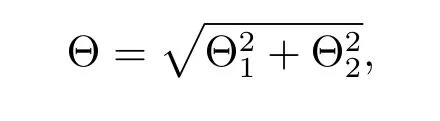
where

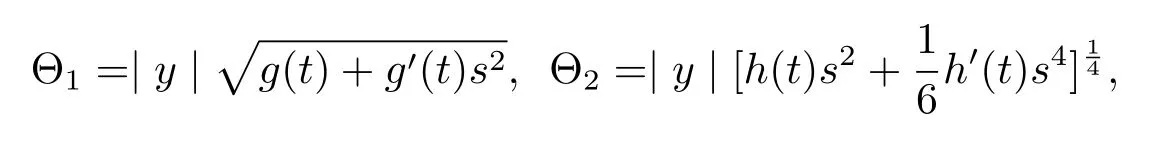
where

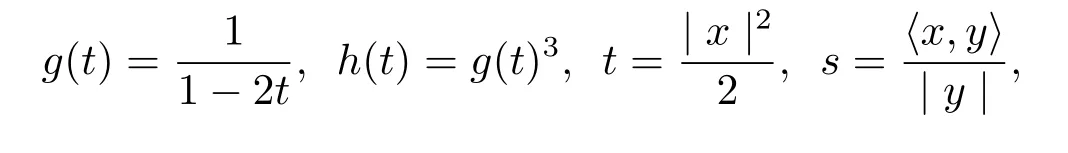
here Θ1and Θ2satisfy(1.1)by straightforward calculations.It’s easy to see that if Θ1and Θ2satisfy(1.1)thenis also a solution of(1.1)where a,b are non-negative constants.After noting this interesting fact,the two authors discussed the solution of dually flat Eq.(1.1)in the following forms

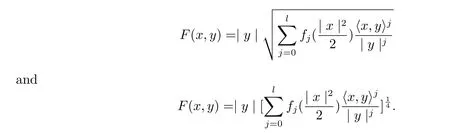
On the other hand,there is a new example of non-Riemmannian dually flat Finsler metrics given in[5,8],

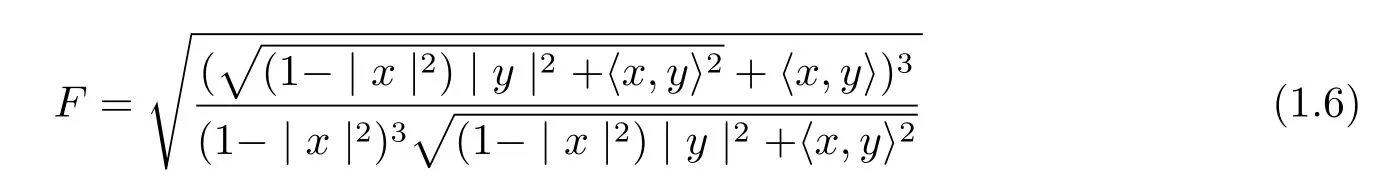
on the unit ball Bm(μ),where y∈TxBm?Rm.The metric F can be expressed in the form

where

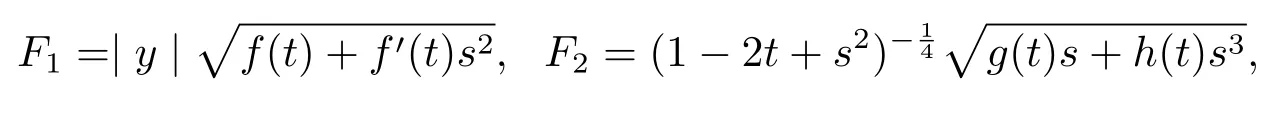
where

We can verify that F1and F2satisfy(1.1)by direct calculations.

Inspired by the results achieved in[6],the fundamental property of the dually flat eq.(1,1)and the metric given in(1.6),in this papar,we try to find the solution of the dually flat eq.(1.1)in the following forms

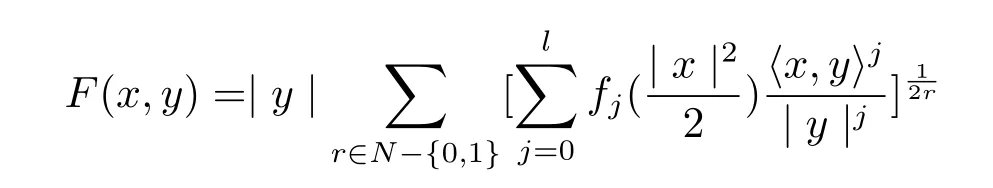
and

By the solutions we find,a lot of new dually flat Finsler metrics can be constructed.Through caculations,we have the following conclusions.

Theorem 1.1Let f(t,s)be a function defined by

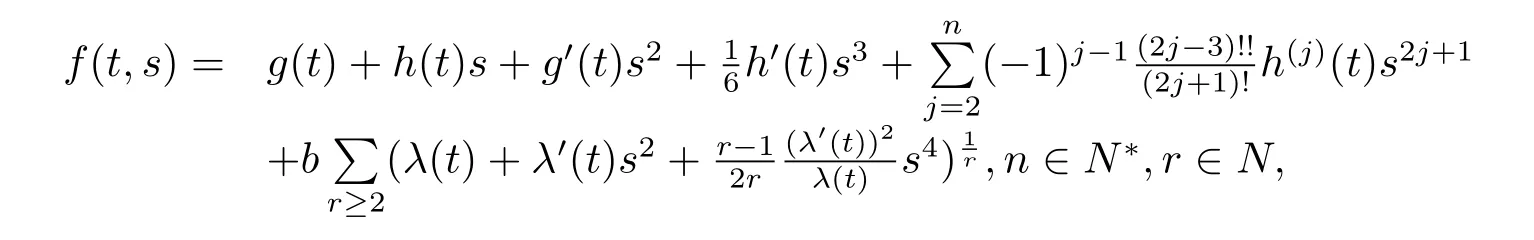
where b is a constant and g(t)and λ(t)are any differentiable functions.h(t)is an any polynomial function of N degree where N≤n and h(j)denotes the j-order derivative for h(t).Then the following spherically symmetric Finsler metric on Bm(μ),

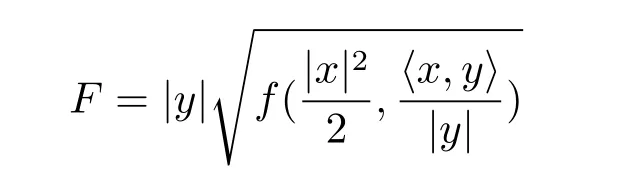
is dually flat if and only if r=2.

Theorem 1.2Let f(t,s)be a function defined by

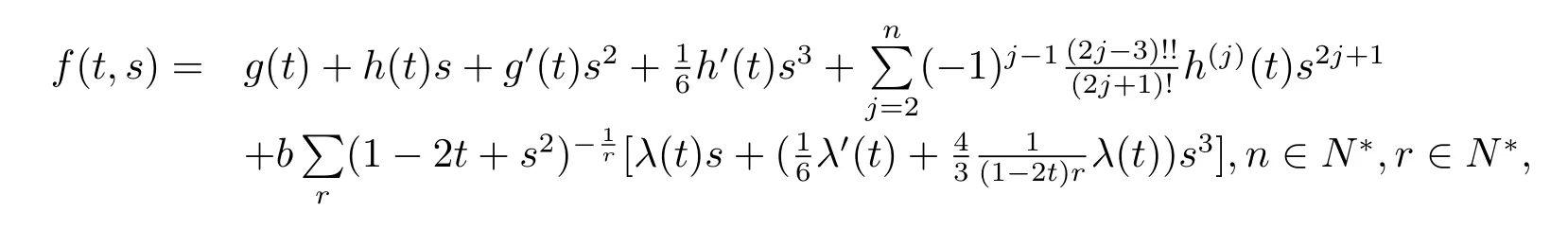
where b is a constant and g(t)and λ(t)are any differentiable functions,h(t)is an any polynomial function of N degree where N≤n and h(j)denotes the j-order derivative for h(t).Then the following spherically symmetric Finsler metric on Bm(μ),

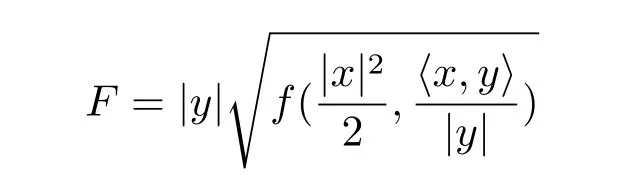
is dually flat if and only if r=2,at this time,

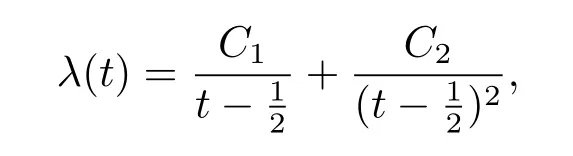
where C1,C2are constants.

Remark 1Let us take a look at a special case b=1,C1=0,C2=3,settingh(t)=0,the metric in Theorem 1.2 is given by

It is also obtained by Li[5]and Yu[8]in other different ways.

2 Proof of Theorem 1.1

Lemma 2.1[6]F=|y|is a solution of(1.1)if and only if f satisfies

The solution f of(2.1)where f=f(t,s)given by f(t,s)=was discussed in[6].Meanwhile,the following propositions were obtained.

Proposition 2.1F=|y|in the form

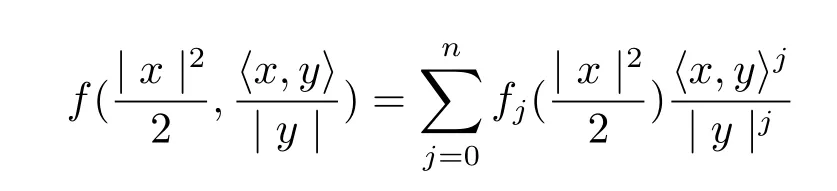
is a solution of the dually flat eq.(2.1)if and only if f(t,s)satisfies

and

Proposition 2.2We have the following solutions of(2.1),

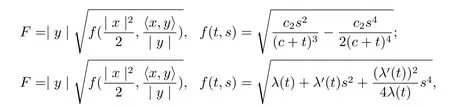
where λ(t)is an any differentiable function.

Now let us consider the solution given by

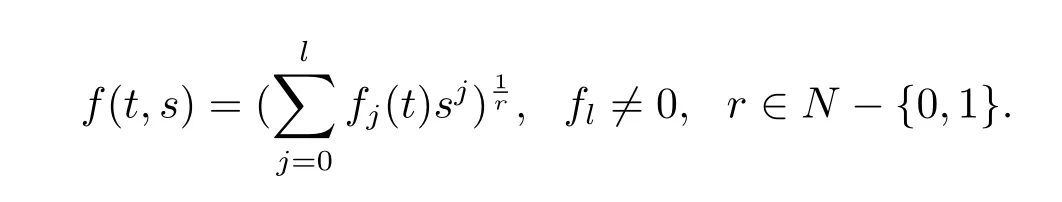
By a direct calculation,

Putting together(2.2),(2.3),(2.4),we have

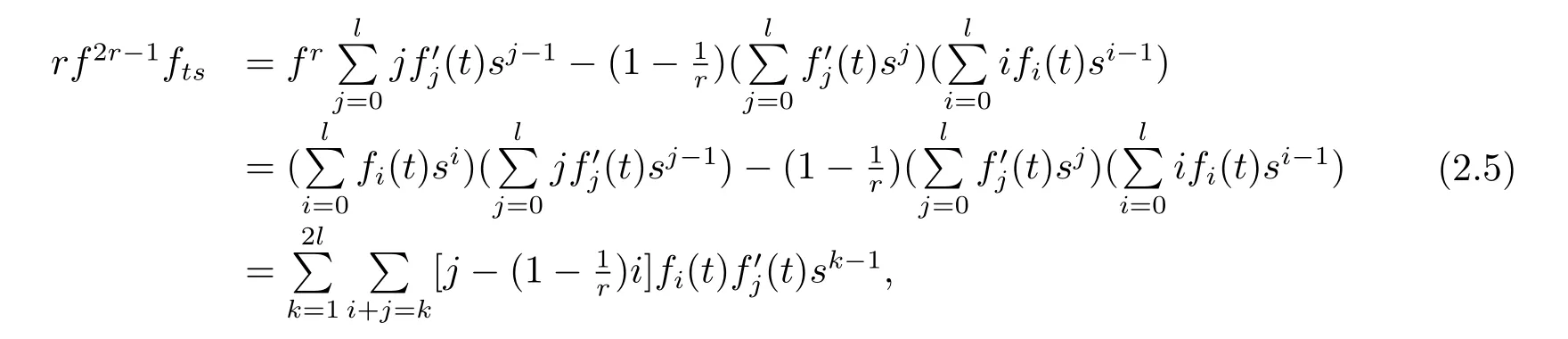
here we use of the following lemma.

Lemma 2.2We have the following equations

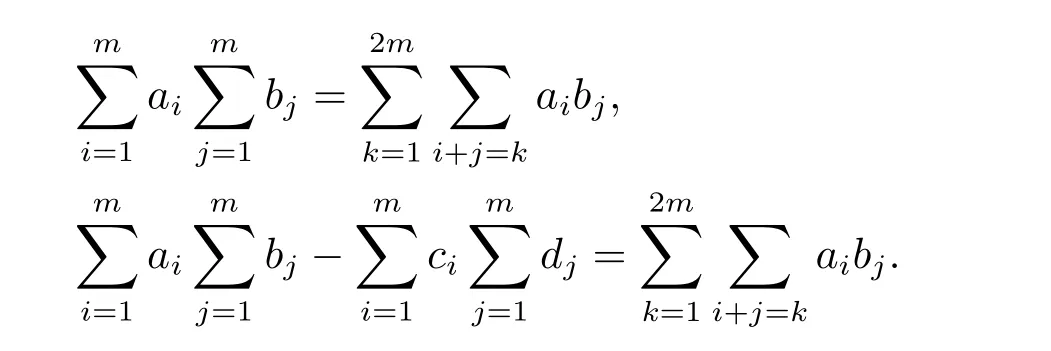
Differentiating(2.3),we get

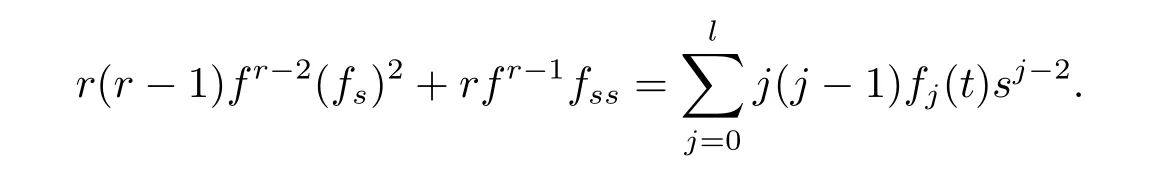
Similarity,by using Lemma 2.2,we have

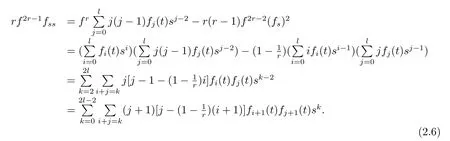
By using(2.2)and Lemma 2.2,we obtain

Putting together(2.5),(2.6),(2.7),we have the following

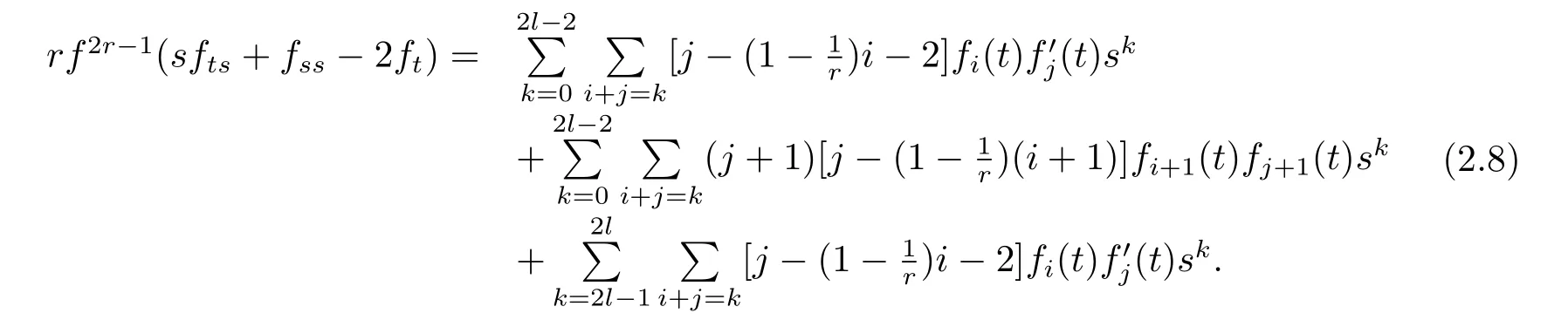
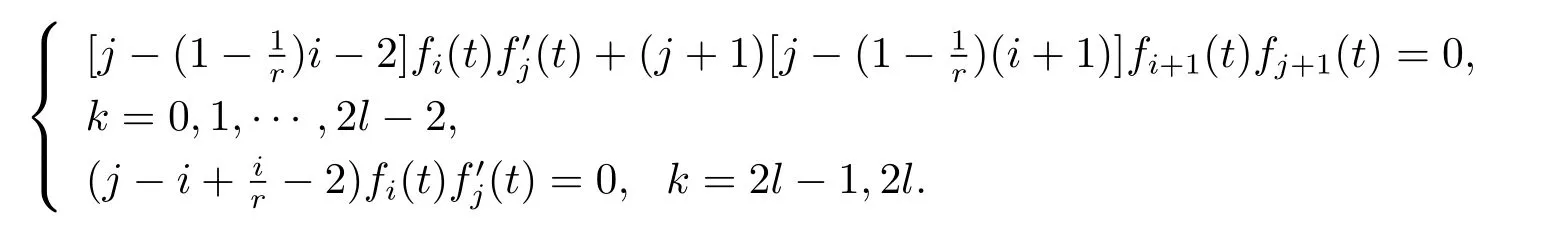
Let us focus on a special case l=4 and f1(t)=f3(t)=0,then

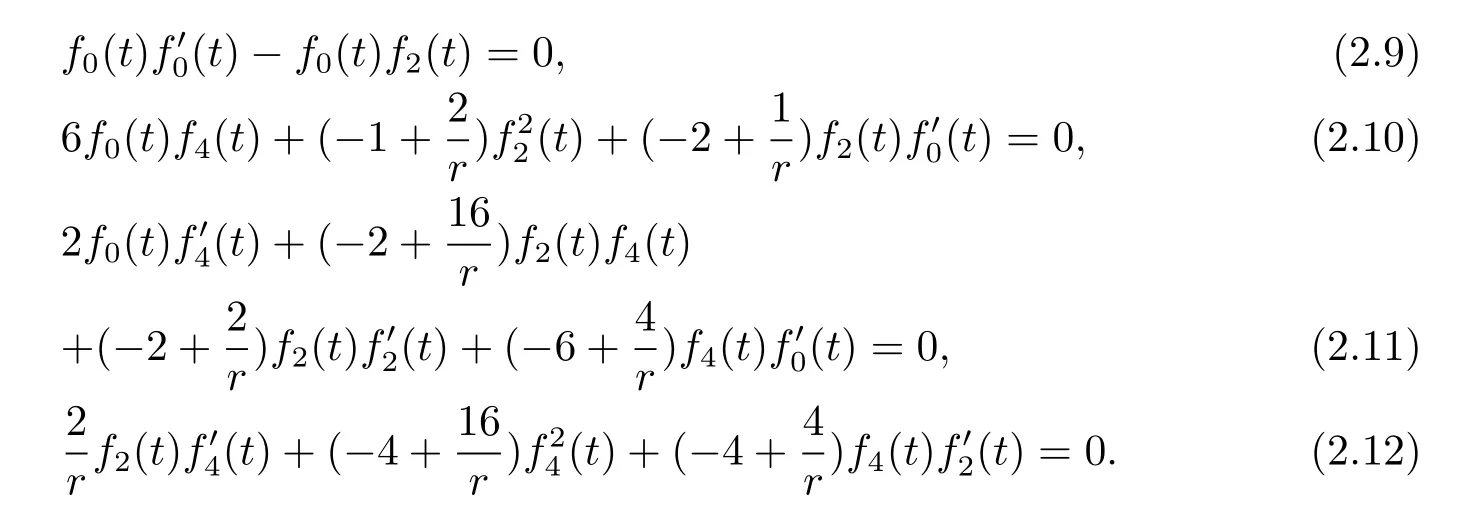
From(2.9),we know

or

Case 1Plugging(2.14)to(2.10)we get

Substituting(2.14),(2.15)into(2.11)yields

Putting(2.14),(2.15),(2.17)into(2.12),the equality holds.Then

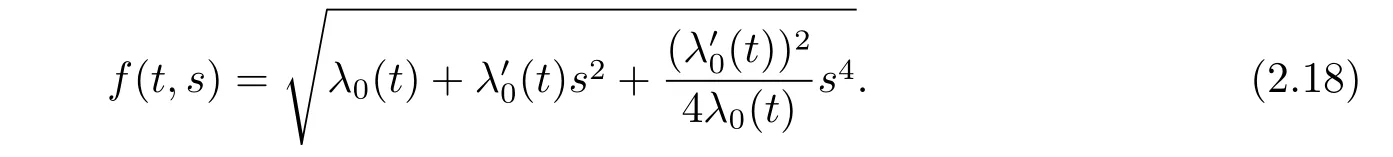
Case 2Plugging(2.13)to(2.10)we know

If r=2,the results are the same as Mo’s in[9].If rf0=f2=0,f4is an arbitrary function.

Combine Propositions 2.1,2.2,(2.17),(2.18)and the fundamental property of the dually flat eq.(1.1),Theorem 1.1 can be achieved.

3 Proof of Theorem 1.2

In this section,we are going to construct more dually flat Finsler metrics.Consider the spherically symmetric Finsler metric F=|y|on Bm(μ)where f=f(t,s)is given by

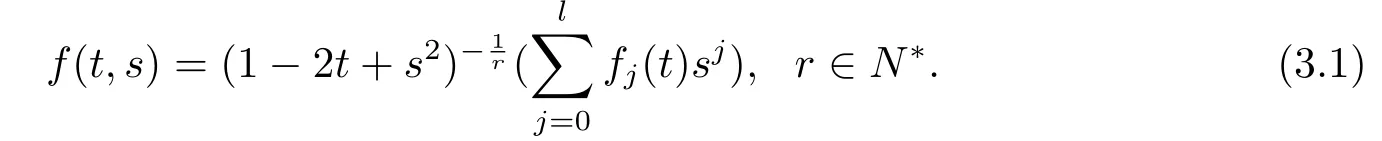
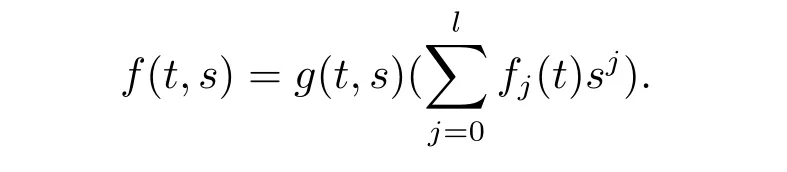
Thus

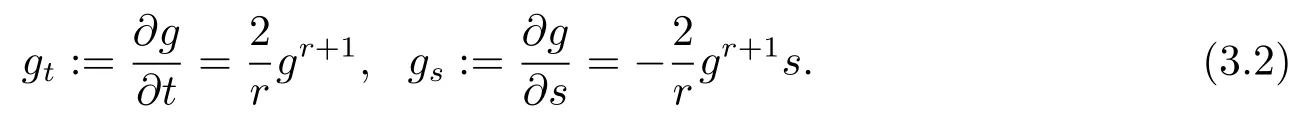
Differentiating(3.1),by using(3.2),we get

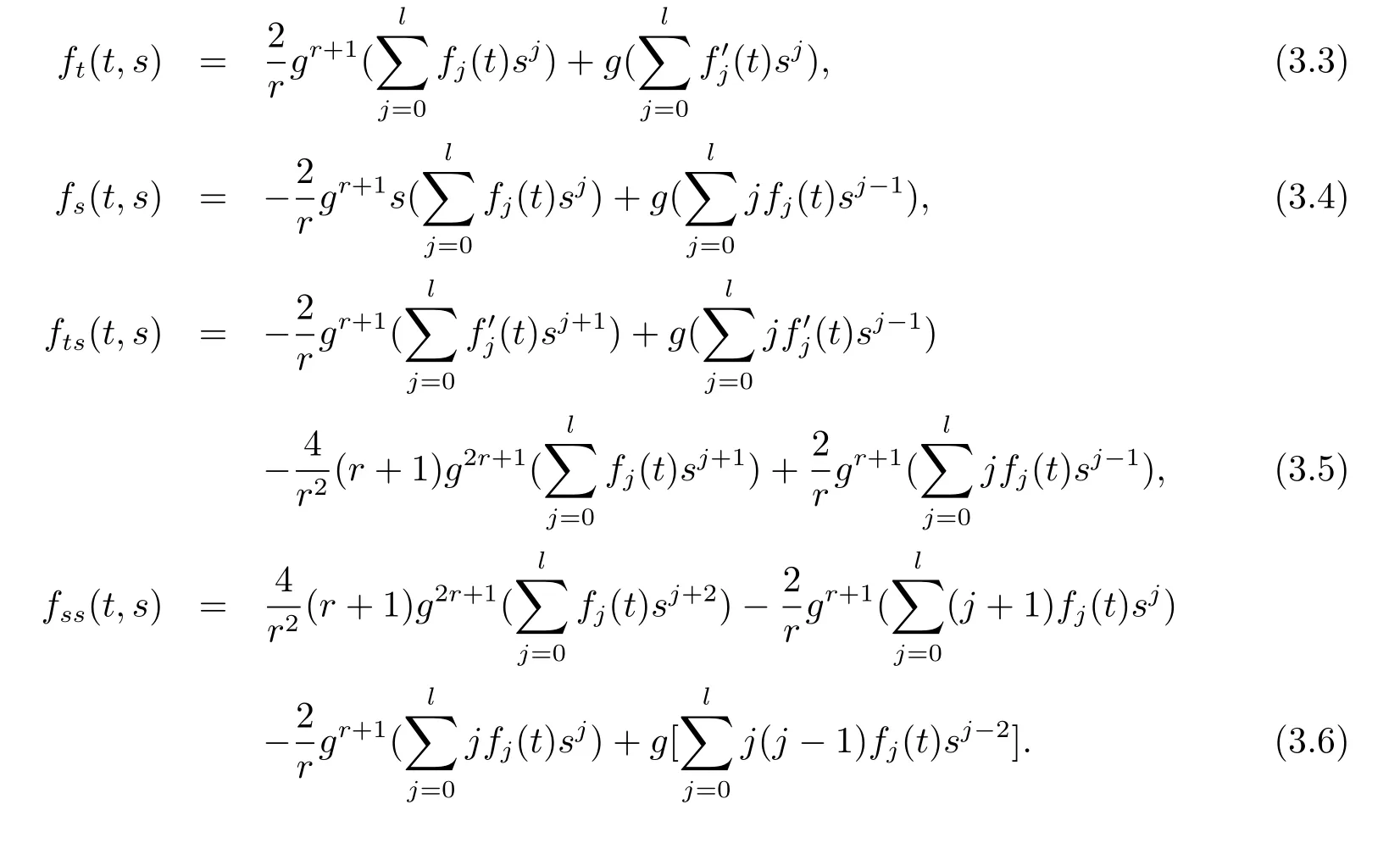
Plugging(3.3),(3.5),(3.6)into the dually flat eq.(2.1)we get the following

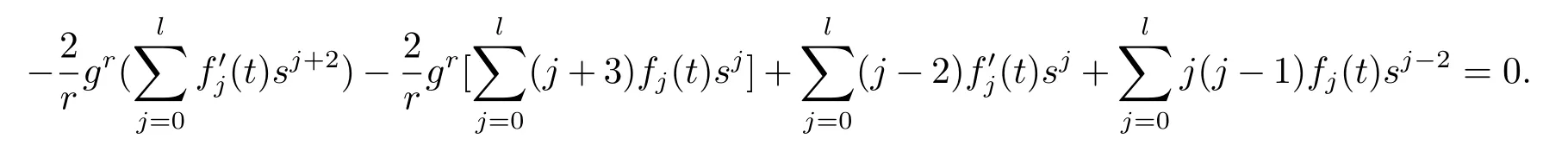
Multiplying g-ron the above equation,then

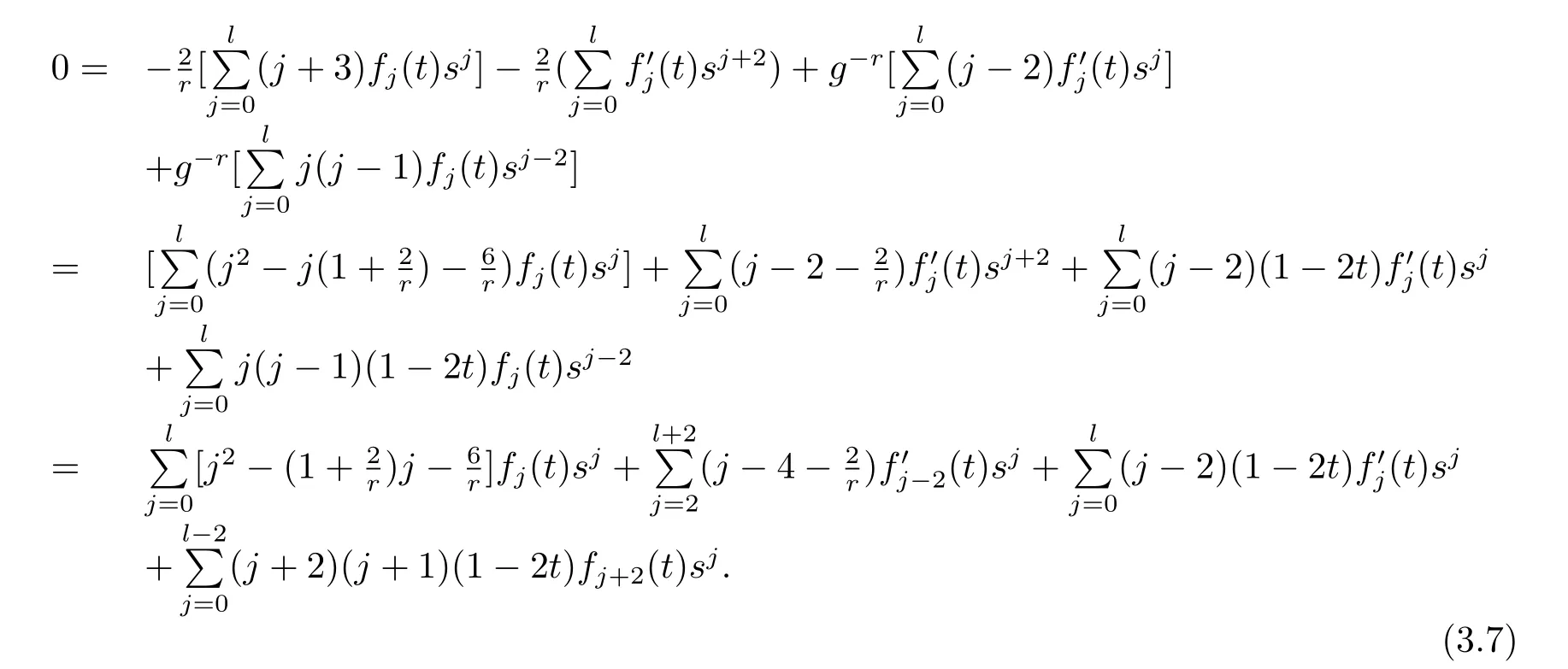
From(3.7),we obtain the following equations

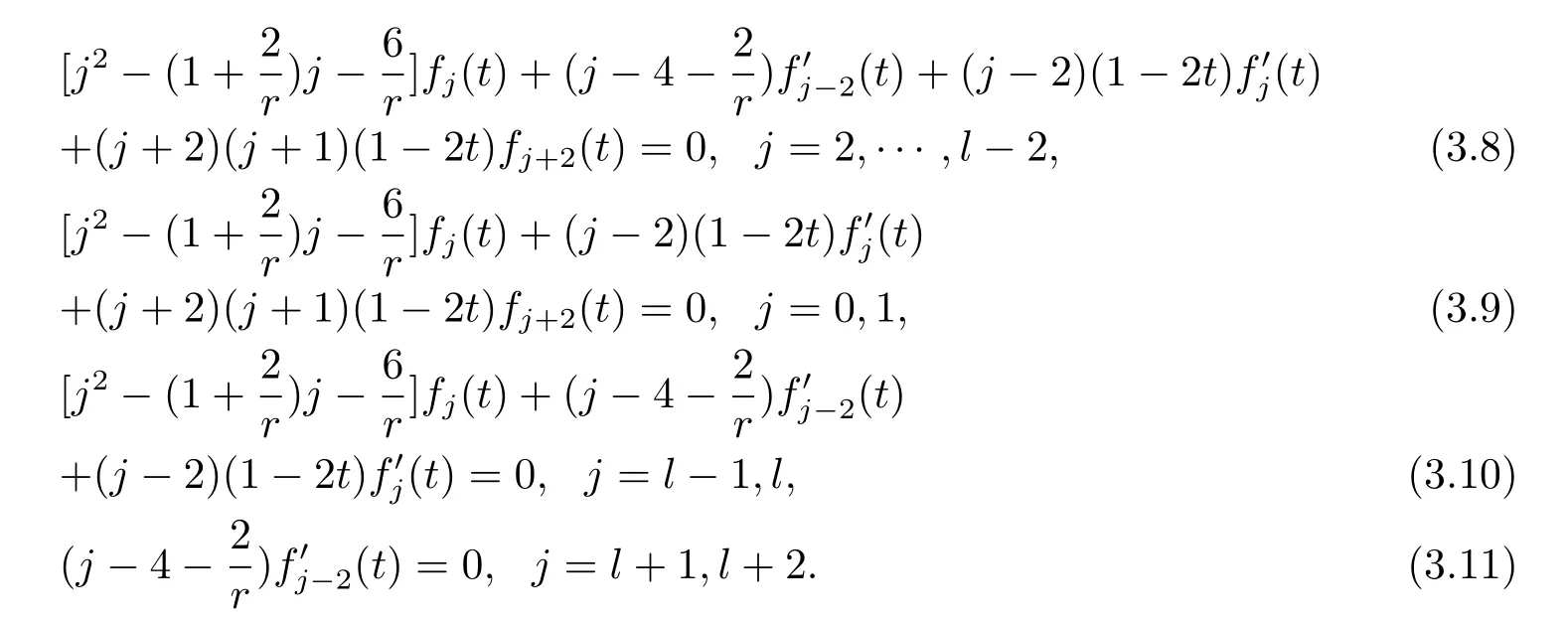
Let us take a look at a special case l=4,f2(t)=f4(t)=0,then

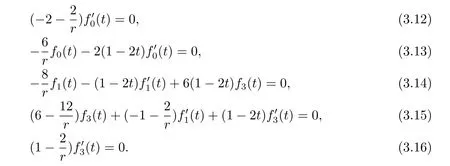
From(3.12),we know that

Plugging(3.17)into(3.13),

From(3.14),we obtain

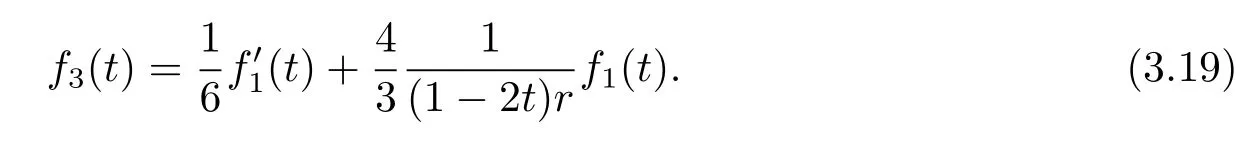
Differentiating(3.19),

Substituting(3.19),(3.20)into(3.15)yields

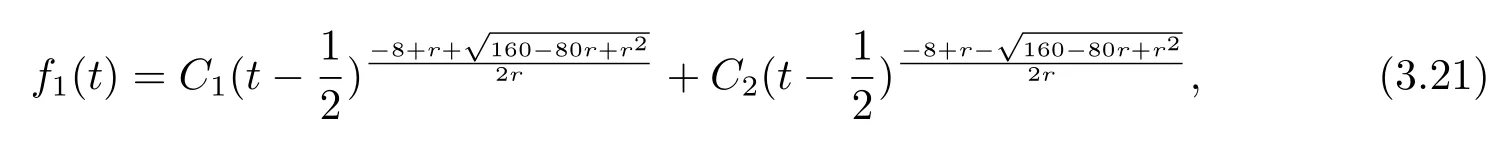
where C1,C2are constants.Plugging(3.20)into(3.16),if

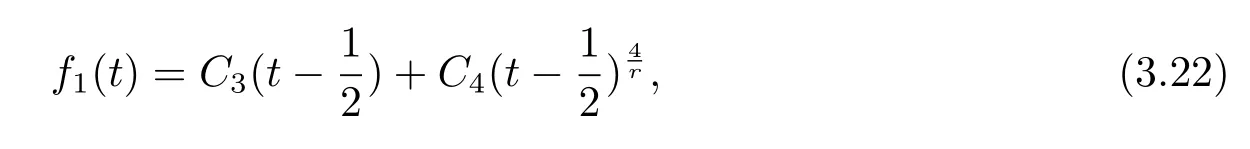
where C3,C4are constants.Obviously,f1(t)in(3.21)and f1(t)in(3.22)are not the same. Thus

Meanwhile,substituting(3.23)into(3.21),we obtain

Though the above analysis,we get the following proposition.

Proposition 3.1We have the following solutions of(2.1),

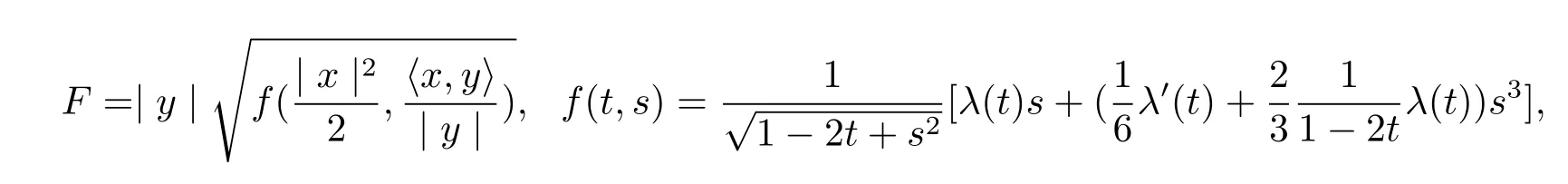
where λ(t)satisfies

Combine Propositions 2.1,3.1,(3.23)and the fundamental property of the dually flat eq.(1.1),Theorem 1.2 can be achieved.

AcknowledgementsWe would like to take this opportunity to thank Professor Mo Xiaohua for the discussions held on this topic.

[1]Amari S I,Nagaoka H.Methods of information geometry[M].Oxford:American Math.Soc.,2001.

[2]Shen Zhongmin.Riemann-Finsler geometry with applications to information geometry[J].Chinese Ann.Math.,Series B,2006,27(1):73–94.

[3]Cheng Xinyue,Shen Zhongmin,Zhou Yusheng.On locally dually flat Finsler metrics[J].Intern.J. Math.,2010,21(11):1531–1543.

[4]Xia Qiaoling.On locally dually flat(α,β)-metrics[J].Differ.Geo.Appl.,2011,29(2):233–243.

[5]Li Benling.On dually flat Finsler metrics[J].Differ.Geo.Appl.,2013,31(6):718–724.

[6]Huang Libing,Mo Xiaohuan.On some explicit constructions of dually flat Finsler metrics[J].J. Math.Anal.Appl.,2013,405(2):565–573.

[7]Cheng Xinyue,Zhang Ting,Yuan Mingao.On dually flat and conformally flat(α,β)-metrics[J].J. Math.,2014,34(3):417–422.

[8]Yu Changtao.On dually flat general(α,β)-metrics[J].arXiv preprint,arXiv:1401.0061,2013.

[9]Yu Changtao.On dually flat(α,β)-metrics[J].J.Math.Anal.Appl.,2014,412(2):664–675.

[10]Huang Libing,Mo Xiaohuan.Projectively flat Finsler metrics with orthogonal invariance[J].Ann. Pol.Math.,107(2013):259–270.

[11]Rutz S.Symmetry in Finsler spaces[J].Contem.Math.,1996,196:289–300.

[12]Yu Changtao,Zhu Hongmei.On a new class of Finsler metrics[J].Differ.Geo.Appl.,2011,29(2): 244–254.

[13]Mo Xiaohuan,Zhou Linfeng.The curvatures of spherically symmetric Finsler metrics in Rn[J]. arXiv:1202.4543.

[14]Zhou Linfeng.Projective spherically symmetric Finsler metrics with constant flag curvature in Rn[J]. Geo.Dedicata,2012,158(1):353–364.

[15]Mo Xiaohuan,Zhu Hongmei.On a class of projectively flat Finsler metrics of negative constant flag curvature[J].Intern.J.Math.,2012,23(08):125008.p.14.

[16]Guo Enli,Liu Huaifu,Mo Xiaohuan.On spherically symmetric Finsler metrics with isotropic Berwald curvature[J].Intern.J.Geo.Meth.Modern Phy.,2013,10(10):603–610.

[17]Yu Changtao.On dually flat Randers metrics[J].Nonl.Anal.:The.,Meth.Appl.,2014,95:146–155.

一類對偶平坦的球?qū)ΨQ的芬斯勒度量

陳亞力,宋衛(wèi)東

(安徽師范大學(xué)數(shù)學(xué)計算機(jī)科學(xué)學(xué)院,安徽蕪湖241000)

本文研究了對偶平坦的芬斯勒度量的構(gòu)造問題.通過分析球?qū)ΨQ的對偶平坦的芬斯勒度量的方程的解,我們構(gòu)造了一類新的對偶平坦的芬斯勒度量,并得到了球?qū)ΨQ的芬斯勒度量成為對偶平坦的充分必要條件.

對偶平坦;芬斯勒度量;球?qū)ΨQ

O186.1

tion:53B40;53C60;58B20

A

0255-7797(2017)01-0107-11

?Received date:2014-07-02Accepted date:2014-12-22

Foundation item:Supported by the National Natural Science Foundation of China(Grant 11071005).

Biography:Chen Yali(1990–),femal,born at Wuhu,Anhui,major in differential geometry and its applications.