LONG Pin-hong,HAN Hui-li

(School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China )

MAJORIZATION OF THE GENERALIZED MARTIN FUNCTIONS FOR THE STATIONARY SCHRDINGER OPERATOR AT INFINITY IN A CONE

LONG Pin-hong,HAN Hui-li

(School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China )

In the paper,we mainly study Dirichlet problem for the stationary Schrdinger operator and the boundary behavior of Martin function.Depended on the generalized Martin representation and the fundamental system of solutions of an ordinary differential equation corresponding to stationary Schrdinger operator,we obtain some characterizations for the majorization of the generalized Martin functions associated with the stationary Schrdinger operator in a cone with smooth boundary,and generalize some classical results in Laplace setting.

stationary Schrdinger operator;Martin function;harmonic majorization;minimally thin;cone

1 Introduction

Let Rn(n≥2)be the n-dimensional Euclidean space and S its an open set.The boundary and the closure of S are denoted by?S and,respectively.In cartesian coordinate a point P is denoted by(X,xn),where X=(x1,x2,···,xn-1).For P and Q in Rn,let|P|be the Euclidean norm of P and|P-Q|the Euclidean distance.The unit sphere and the upper half unit sphere are denoted by Sn-1and,respectively.For P∈Rnand r＞0,let B(P,r)be the open ball of radius r centered at P in Rn,then Sr=?B(O,r).Furthermore, denote by dSrthe(n-1)-dimensional volume elements induced by the Euclidean metric on Sr.

In the paper we are mainly concerned with some properties for the generalized Martin function associated with the stationary Schrdinger operator in a cone.Our aim is to give precise characterization for majorization of the generalized Martin functions in a cone.Deng et al.(see[17]and[23])ever considered the growth for the potential functions in the half space.However,Miyamoto et al.(see[10,11]and[12])focused on the potential theoriesin a cone.Levin and Kheyfits(see[9])paid attention to the problems associated with the stationary Schrdinger operator in a cone.In addition,Long and Qiao et al.(see[7,8,13–15]and[16])considered some related problems about Dirichlet problem for the stationary Schrdinger operator at∞with respect to a cone as well as Levin and Kheyfits(see[9]). Based on the above statement,we will mainly generalize some results from Miyamoto and Yoshida(see[10])to the stationary Schrdinger operator’s setting.Unfortunately we don’t have Riesz-Herglotz type theorem as the classical results which needed in the proof.To get over this difficulty,here we will depend on the generalized Martin representation theorem (see[8]).For the better statements about our results,we will introduce some notations and background materials below.

Relative to system of spherical coordinates,the Laplace operator Δ may be written by

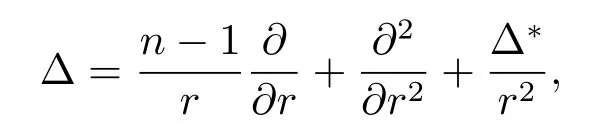
where the explicit form of the Beltrami operator Δ?is given by Azarin(see[1]).

For an arbitrary domain D in Rn,ADdenotes the class of nonnegative radial potentials a(P),i.e.,0≤a(P)=a(r),P=(r,Θ)∈D,such that a∈(D)with some b＞n/2 if n≥4 and with b=2 if n=2 or n=3.

If a∈AD,then the stationary Schrdinger operator with a potential a(·)

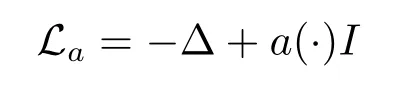
can be extended in the usual way from the space(D)to an essentially self-adjoint operator on L2(D),where Δ is the Laplace operator and I the identical operator(see[18,Chap.13]). Then Lahas a Green a-function(·,·).Here(·,·)is positive on D and its inner normal derivative(·,·)/?nQis not negative,where?/?nQdenotes the differentiation at Q along the inward normal into D.We write this derivative by(·,·),which is called the Poisson a-kernel with respect to D.Denote by(·,·)the Green function of Laplacian.

For simplicity,a point(1,Θ)on Sn-1and the set{Θ;(1,Θ)∈?}for a set ?(??Sn-1) are often identified with Θ and ?,respectively.For two sets?R+and ??Sn-1,the set {(r,Θ)∈Rn;r∈,(1,Θ)∈?}in Rnis simply denoted by×?.In particular,the half space R+×={(X,xn)∈Rn;xn＞0}will be denoted by Tn.By Cn(?)we denote the set R+×? in Rnwith the domain ? on Sn-1and call it a cone.We mean the sets I×? and I×?? with an interval on R+by Cn(?;I)and Sn(?;I),and Cn(?)∩Srby Cn(?;r).By Sn(?)we denote Sn(?;(0,+∞)),which is?Cn(?){O}.From now on,we always assume D=Cn(?)and write

Let ? be a domain on Sn-1with smooth boundary and λ the least positive eigenvalue for-Δ?on ?(see[19,p.41]),

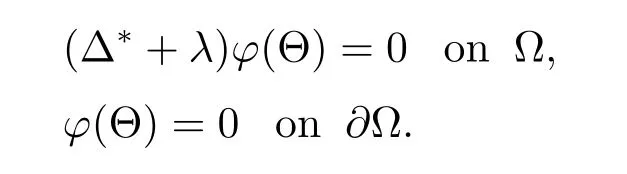
The corresponding eigenfunction is denoted by φ(Θ)satisfying=1.In order to ensure the existence of λ and φ(Θ),we put a rather strong assumption on ?:if n≥3, then ? is a C2,α-domain(0＜α＜1)on Sn-1surrounded by a finite number of mutually disjoint closed hypersurfaces(e.g.,see[6,p.88–89]for the definition of C2,α-domain).

Solutions of an ordinary differential equation

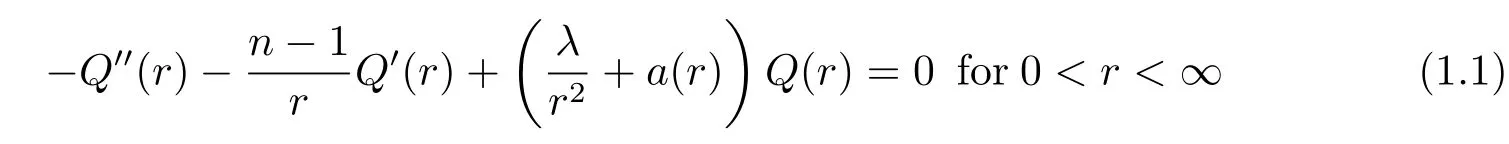
are known(see[22]for more references)that if the potential a∈AD.We know the equation (1.3)has a fundamental system of positive solutions{V,W}such that V is nondecreasing with

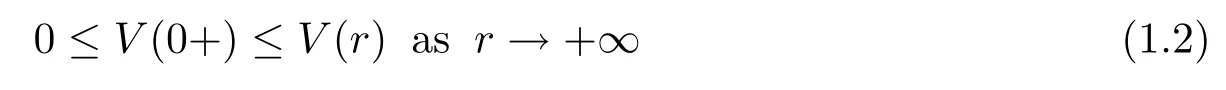
and W is monotonically decreasing with

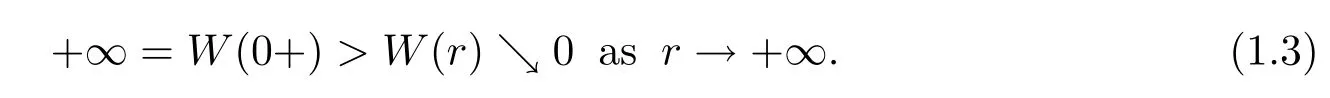
We remark that both V(r)φ(Θ)and W(r)φ(Θ)are a-harmonic on Cn(?)and vanish continuously on Sn(?).

We will also consider the class BD,consisting of the potentials a∈ADsuch that there exists the finite limit=κ∈[0,∞),moreover,r-1|r2a(r)-κ|∈L(1,∞).If a∈BD,then the(super)subfunctions are continuous(e.g.see[20]).For simplicity,in the rest of paper we assume that a∈BD.

Denote

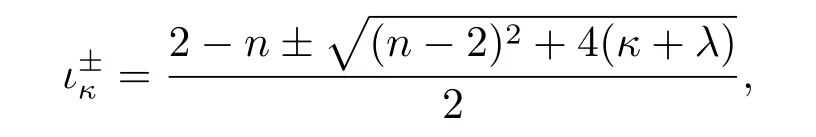
then the solutions V(r)and W(r)to equation(1.1)normalized by V(1)=W(1)=1 have the asymptotic(see[6])

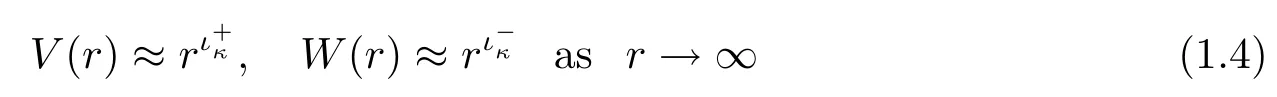
and

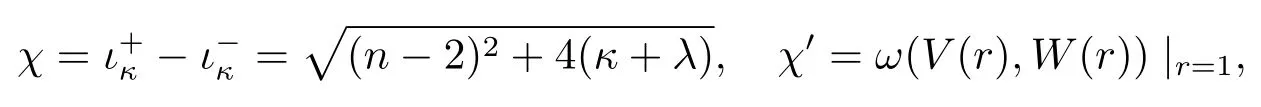
where χ′is their Wronskian at r=1.

Remark 1If a=0 and ?=where snis the surface area 2πn/2{Γ(n/2)}-1of Sn-1.

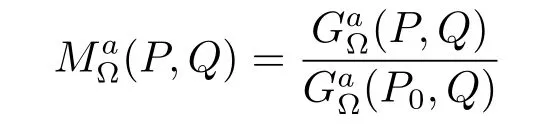
is called the generalized Martin kernel of Cn(?)(relative to P0).If Q=P0,the above quotient is interpreted as 0(for a=0,refer to Armitage and Gardiner[3]).

The rest of the paper is organized as follows:in Section 2,we shall give our main theorems;in Section 3,some necessary lemmas are given;in Section 4,we shall prove the main results.

2 Statement of Main Results

It is known that the Martin boundary△of Cn(?)is the set?Cn(?)∪{∞}.When we denote the Martin kernel associated with the stationary Schrdinger operator byCn(?),Q∈?Cn(?)∪{∞})with respect to a reference point chosen suitably,for any P∈Cn(?),we see

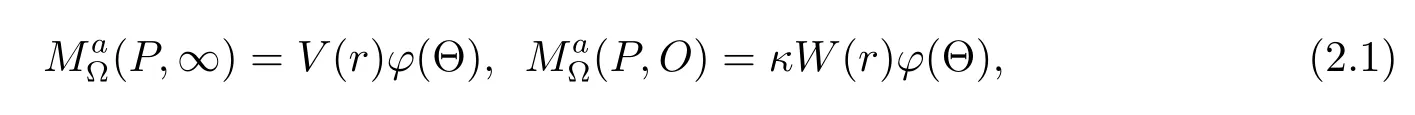
where O denotes the origin of Rnand κ is a positive constant.

For a set E?D and ?∈(0,1),put

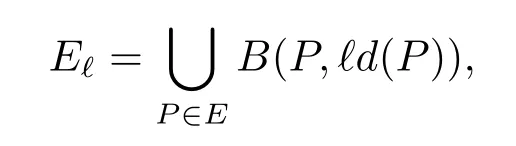
Theorem 1Let E be a set in Cn(?)satisfying∩?Cn(?)=φ.If E?with a positive number ?(0＜?＜1)is a-minimally thin at∞,then there exists a positive generalized harmonic function u(P)on Cn(?)such that

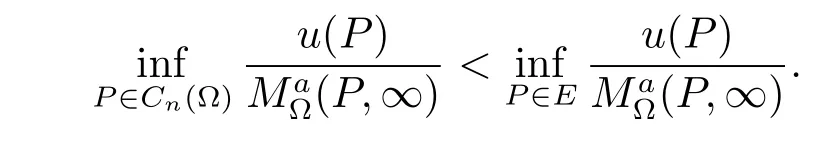
For E?Cn(?)and a fixed point Q∈?Cn(?),E is a-minimally thin at Q if and only ifis the regularized reduced function of(·,Q)relative to E and a superfunction on Cn(?)(refer to[8]).

Following the Armitage and Kuran(see[4])as well as Miyamoto et al.(see[10]),we call that set E?D characterizes the positive generalized harmonic majorization of(·,Q), if every positive generalized harmonic function υ in D which majorizes(·,Q)on E can majorize(·,Q)on D,that is to say

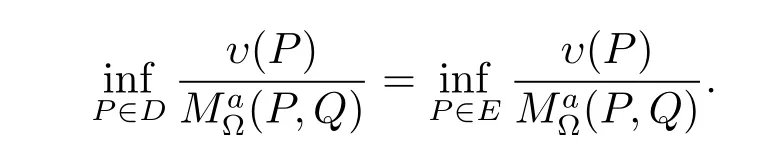
Theorem 2Let E be a subset Cn(?).The following conditions on E are equivalent:

(a)E characterizes the positive generalized harmonic majorization of

(b)for any ?∈(0,1),E?is not a-minimally thin at∞;

(c)for some ?∈(0,1),E?is not a-minimally thin at∞.

Theorem 3Let E be a subset Cn(?).The following conditions on E are equivalent:

(a)E characterizes the positive generalized harmonic majorization of

(b)for any ?∈(0,1),

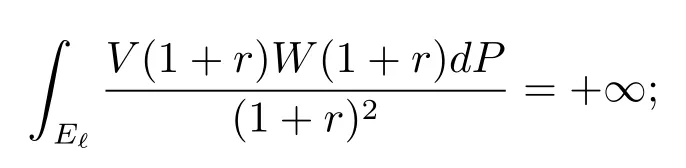
(c)for some ?∈(0,1),

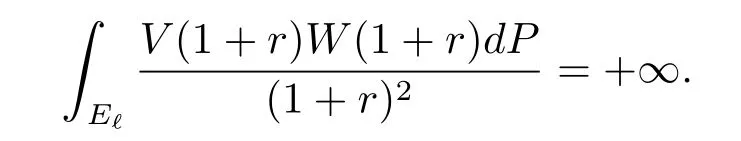
A sequence Pm?D is called to be separated if there exists a positive constant C such that

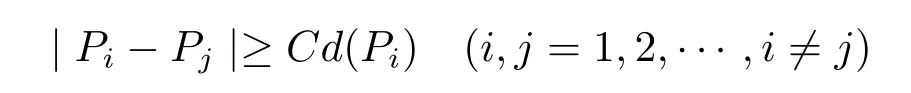
(see[2]).With Theorem 3,we have the corollary as follows.

Corollary 1Let{Pm}?Cn(?)be a separated sequence such that

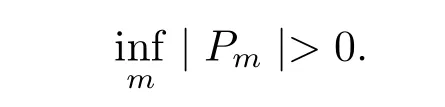
The sequence{Pm}characterizes the positive generalized harmonic majorization ofif and only if

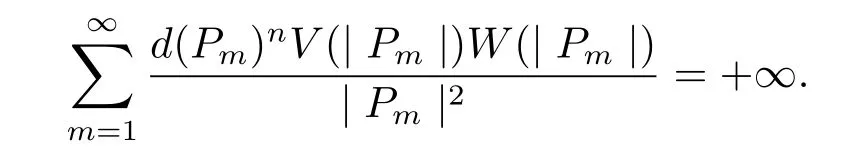
Remark 2When a=0,the theorems and corollary above are due to Miyamoto et al.(see[10]).If a=0 and ?=Theorem 1,Theorem 2 and Theorem 3 are from the Dahlberg’s results in upper-half space or Liapunov-Dini domain in Rn(see[5]),and Corollary 1 results from Armitage and Kuran(see[4]).

3 Some Lemmas

For our arguments we collect the following results.

Lemma 1(see[13])

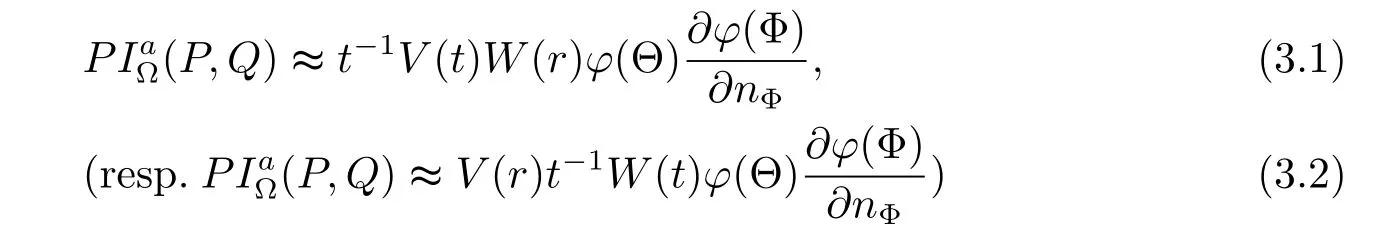
for any P=(r,Θ)∈Cn(?)and any Q=(t,Φ)∈Sn(?)satisfying 0＜

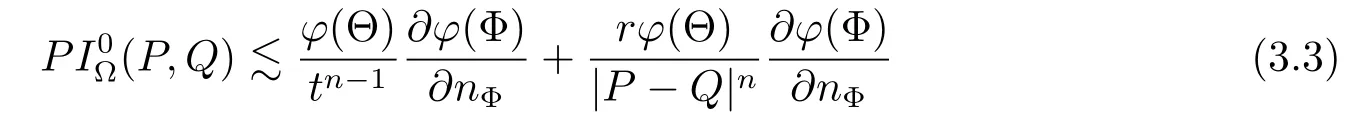
for any P=(r,Θ)∈Cn(?)and any Q=(t,Φ)∈

Lemma 2(see[13])

for any P=(r,Θ)∈Cn(?)and any Q=(t,Φ)∈Sn(?)satisfying 0＜

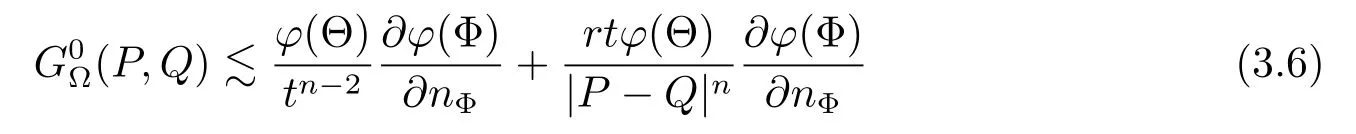
for any P=(r,Θ)∈Cn(?)and any Q=(t,Φ)

Lemma 3(The generalized Martin representation,see[7])If u is a positive a-harmonic function on Cn(?),then there exists a measureμuon△,uniquely determined by u,such that

where△is the Martin boundary of Cn(?).

It is well-known that a cube is of the form

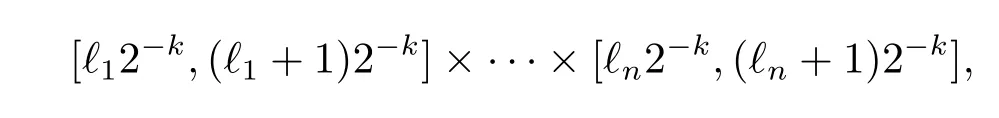
where k,?1,···,?nare integers.Now we introduce a family of so-called Whitney cubes of Cn(?)having the following properties:

(a)∪jWj=Cn(?);

(b)intWj∩intWk=?(jk);

(c)diamWj≤dist(Wj,RnCn(?))≤4diamWj,

where intS,diamS and dist(S1,S2)stand for the interior of S,the diameter of S and the distance between S1and S2,respectively(see[21],P.167,Theorem 1).

Lemma 4(see[10])Let{Wi}i≥1be a family of the Whitney cubes of Cn(?)with ?. Let E be a subset of Cn(?).Then there exists a subsequence{Wim}i≥1of{Wi}i≥1such that

(a)∪mWim?E?;

(b)Wim∩E?/4?(m=1,2,,···),E?/4?∪mWim.

Lemma 5(see[8])Let a Borel subset E of Cn(?)be a-minimally thin at∞with respect to Cn(?).Then we see that

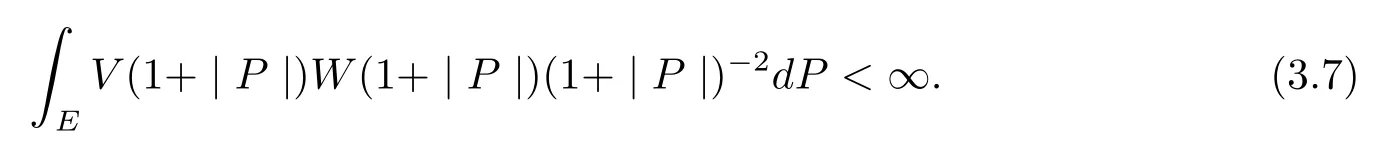
If E is a union of cubes from the Whitney cubes of Cn(?),then(3.7)is also sufficient for E to be a-minimally thin at∞with respect to Cn(?).

4 Proofs of Main Theorems

Proof of Theorem 1When E is a bounded subset of Cn(?),we may assume that u(P)is a constant function.Otherwise we will follow the same method as Dahlberg to make the required function.

Set ?∈(0,1).We assume that{Pm}is a sequence of points Pmwhich are central points of cubes Wimin Lemma 4.From the assumption on E,it follows that{Pm}can notconverge to any boundary point of Cn(?).Since{Pm}∈E?due to Lemma 4,we see that |Pm|→+∞(m→+∞).Because E?is a-minimally thin at∞and

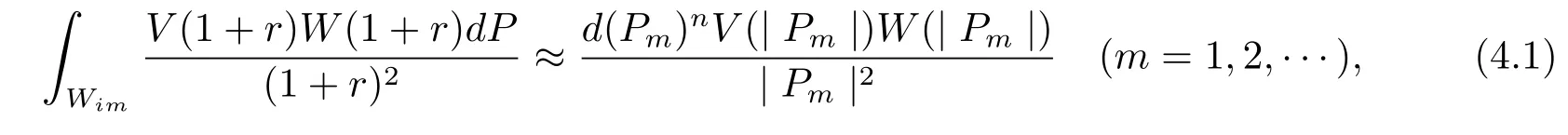
we get by Lemma 4 and Lemma 5 that

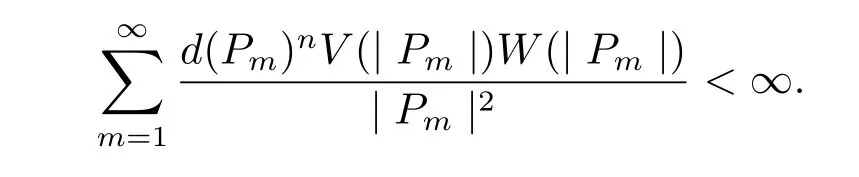
Hence from(1.2)–(1.4)we can take a positive integer N such that d(Pm)≤each m≥N.

Choose a point Qm=(tm,Φm)∈?Cn(?){O}such that

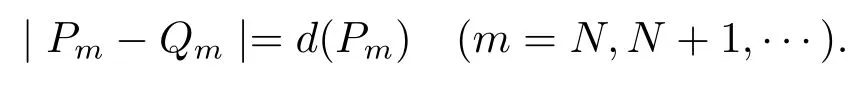
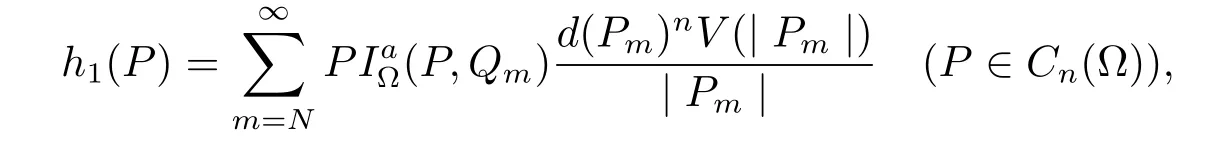
then h1is well defined,and hence is a positive generalized harmonic function on Cn(?)which is due to Lemma 4.

First we will prove that

Denote the Possion Kernel of the ball Bm=B(Pm,d(Pm)))by PIBm(P,Q)for P∈Bmand

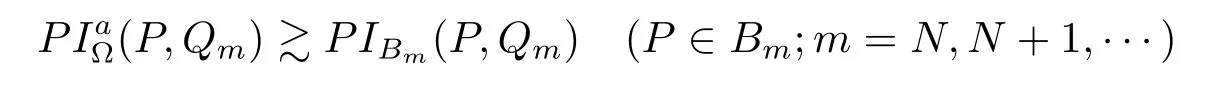
and hence

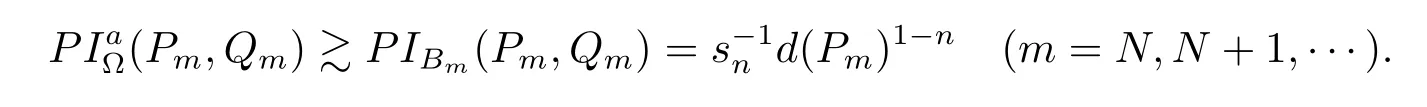
Because

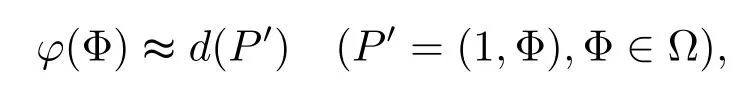
we get that

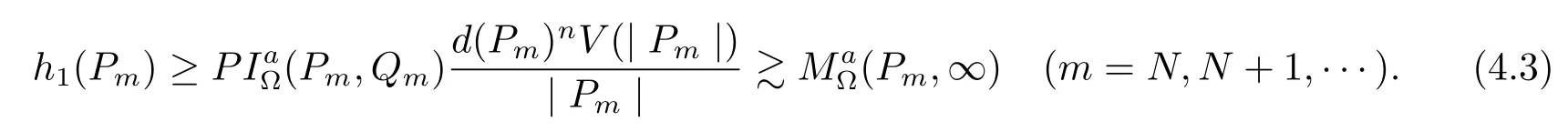
For any P∈E,then exists a point Pmsuch that

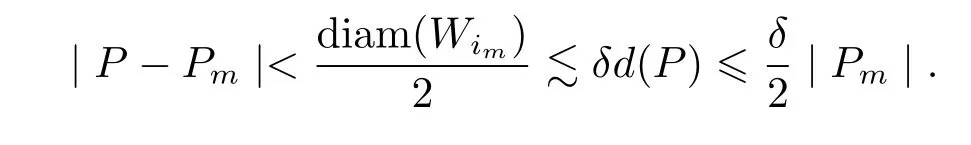
When 2r≤t or r≥2t(2|Pm|≤t or|Pm|≥2t),by Lemma 2 and(1.2)–(1.4)we obtain that

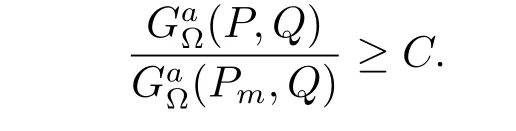
Since

and

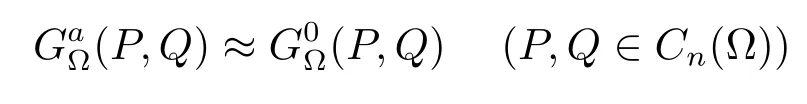
(refer to[10]and[13]),we know that

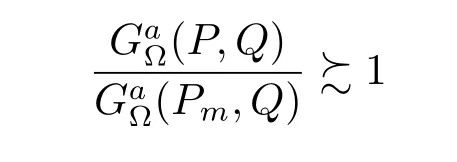
By(2.1)and(1.2)–(1.4)we also see that

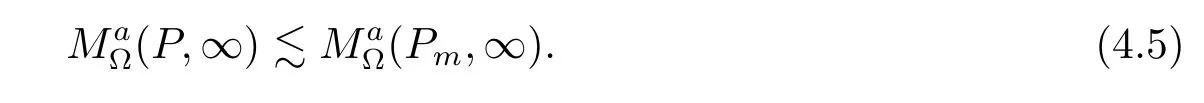
With(4.4)–(4.5)and(4.3)we see that(4.2)holds.

Now,for a fixed ray L which is in Cn(?)and starts from O,we will show

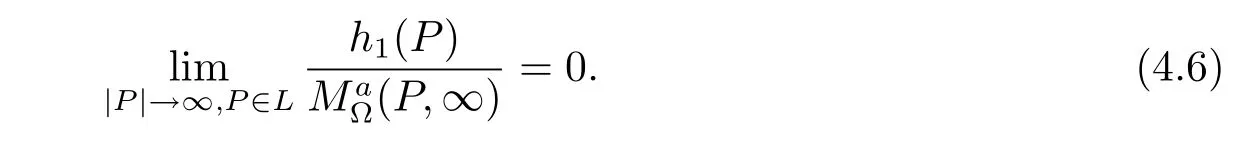
Set

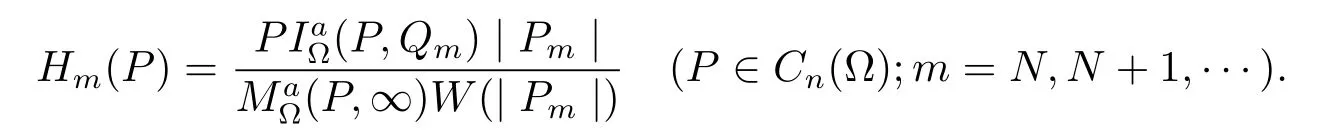
Then we have that

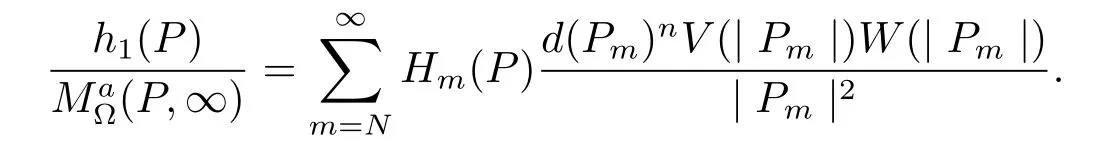
By Lemma 1 we see that

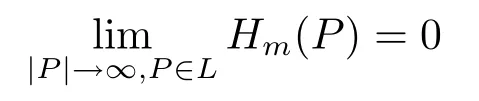
for any fixed m≥N.Hence,if we can show that

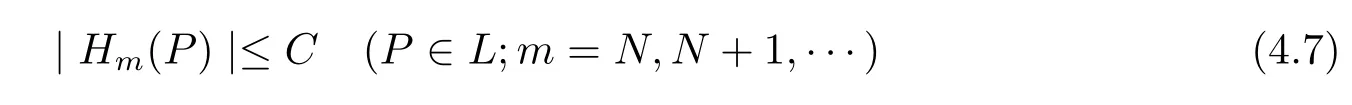
for some constant C independent of m,then we will get(4.6)from(4.1)and Lebesgue’s dominated convergence theorem.

To prove(4.7),we divide the proof into three cases.When 2r≤tmor r≥2tm,by Lemma 1 we see that

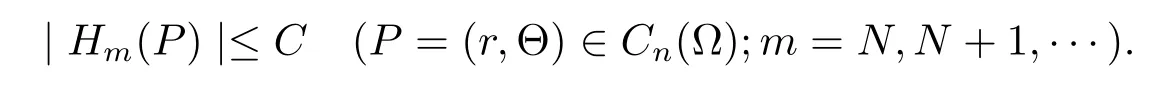
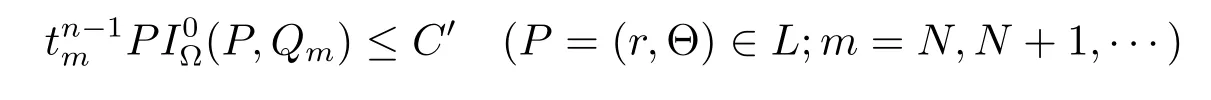
for some constant C′(refer to[10,p.1051]).Sinceby(1.2)–(1.4) we have

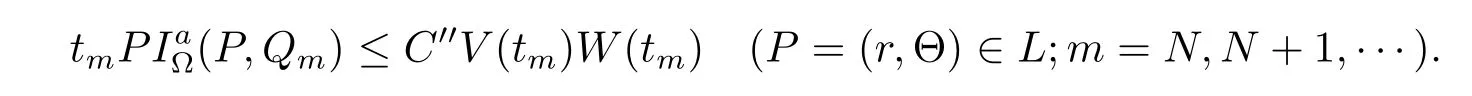
So

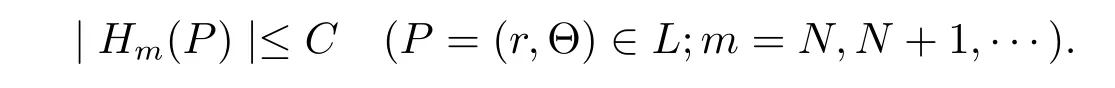
Proof of Theorem 2(a)?(b).Let C be a positive constant and set EC={P∈ E:(P,∞)≥C}.Then ECsatisfies that∩?Cn(?)=?.Since E characterizes the positive generalized harmonic majorization of(P,∞),ECalso characterizes the positive generalized harmonic majorization of(P,∞).Otherwise,there would exists a positive generalized harmonic function υ(P)on Cn(?)satisfying

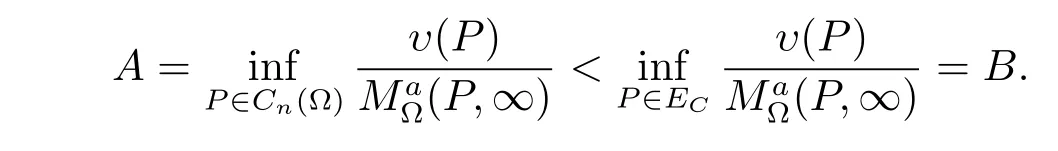
Let u(P)=υ(P)+BC for any P∈Cn(?).Then u(P)≥(P,∞)for P∈E,and so

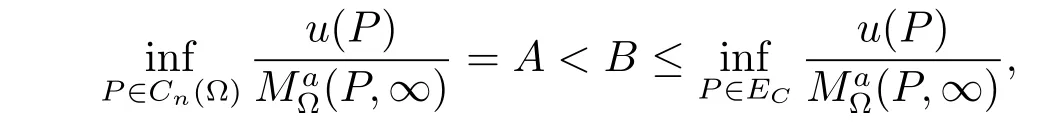
which contradicts(a).

If we can show that(EC)?is not a-minimally thin at infinity when ?∈(0,1),then for all ?∈(0,1)the set E?also is not a-minimally thin at infinity,and hence(b)holds.

Suppose that for some ?∈(0,1)the set(EC)?is a-minimally thin at infinity.Then from Theorem 1 there exists a positive generalized harmonic function υ(P)on Cn(?)satisfying

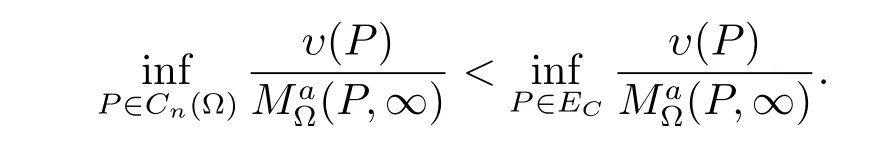
We see that ECcharacterizes the positive generalized harmonic majorization ofso for all ?∈(0,1)the set(EC)?is not a-minimally thin at infinity.

(c)?(a).Suppose that E does not characterize the positive generalized harmonic majorization of(P,∞).Then there exists a positive generalized harmonic function υ(P)on Cn(?)such that

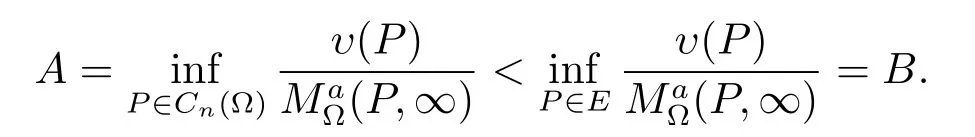
For any P∈E?(?∈(0,1)there exists a point P′such that|P-P′|＜?d(P′),and by the generalized Martin representation and the same proof as Theorem 1 we see that

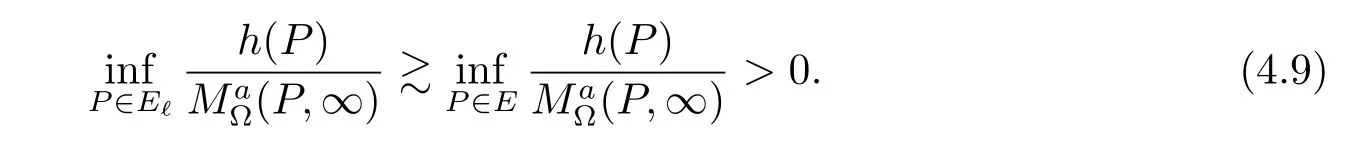
From(4.8)and(4.9)we obtain that

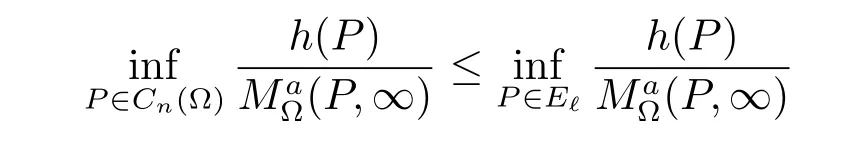
for the positive supfunction h(P)on Cn(?).It follows that E?is a-minimally thin at infinity. This contradicts(c).

Proof of Theorem 3(a)?(b).Assume that

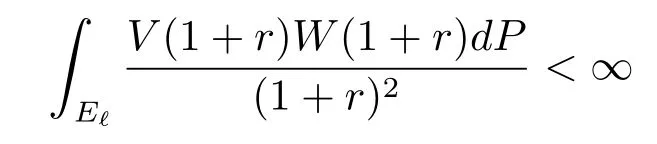
for some ?∈(0,1).Let{Wim}m≥1be a subsequence of{Wi}i≥1from Lemma 4.With(a) of Lemma 4 we obtainZ

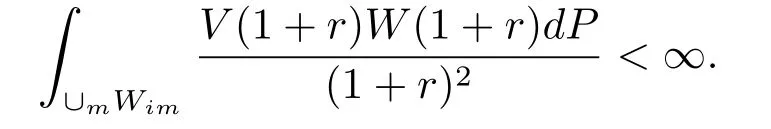
Since∪mWimis a union of cubes from the Whitney cubes of Cn(?)with ?,by Lemma 5 we see that∪mWimis a-minimally thin at infinity.Further,from Lemma 4 we know thata-minimally thin at infinity.

On the other hand,since E characterizes the positive generalized harmonic majorization of(P,∞),we see from the Theorem 2 thatis not a-minimally thin at infinity,which contradicts the conclusion above.

(c)?(a).Suppose that E does not characterize the positive generalized harmonic majorization of(P,∞).Then it follows from Theorem 2 that for any ?∈(0,1)E?is aminimally thin at infinity.So we see from Lemma 5 that for any ?∈(0,1)

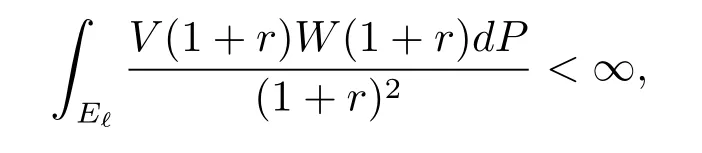
which contradicts(c).

Proof of Corollary 1If{Pm}is a separated sequence,then

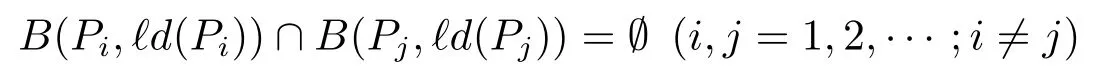
for a sufficiently small ?∈(0,1),and hence

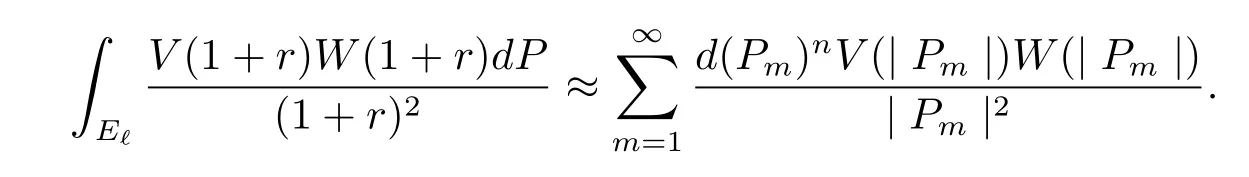
Following(c)of Theorem 3,Corollary 1 immediately holds.

[1]Azarin V S.Generalization of a theorem of Hayman on subharmonic functions in an m-dimensional cone[J].Trans.Amer.Math.Soc.,1969,80(2):119–138.

[3]Armitage D H,Gardiner S J.Classical potential theory[M].London:Springer-verlag,2001.

[5]Dalberg B E J.A minimum principle for positive harmonic functions[J].Proc.London Math.Soc., 1976,33(2):238–250.

[6]Gilbarg D,Trudinger N S.Elliptic partial differential equations of second order[M].Berlin:Springer Verlag,1977.

[7]Long Pinhong,Gao Zhiqiang,Deng Guantie.Criteria of Wiener type for minimally thin sets and rarefied sets associated with the stationary Schrdinger operator in a cone[J].Abstr.Appl.Anal., DOI:10.1155/2012/453891.

[8]Long Pinhong.Characterizations for exceptional sets and growth problems in classical or nonlinear potential theory[D].Beijng:Beijing Normal University,2013.

[9]Levin B,Kheyfits A.Asymptotic behavior of subfunctions of the stationary Schrdinger operator[J]. http://arxiv.org/abs/math/0211328v1,2002,96 pp.

[10]Miyamoto I,Yanagishita M,Yoshida H.On harmonic majorization of the Martin function at infnity in a cone[J].Czech.Math.J.,2005,55(130):1041–1054.

[11]Miyamoto I,Yoshida H.Two criterions of Wiener type for minimally thin sets and rarefied sets in a cone[J].J.Math.Soc.Japan.,2002,54(3):487–512.

[12]Miyamoto I,Yoshida H.On a-minimally thin sets at infinity in a cone[J].Hiroshima Math.J.,2007, 37(1):61–80.

[13]Qiao Lei.Some researches on(generalized)harmonic and superharmonic functions[D].Beijng:Beijing Normal University,2010.

[14]Qiao Lei,Deng Guantie.A theorem of Phragmn Lindelf type for subfunctions in a cone[J].Glasg. Math.J.,2011,53(3):599–610.

[15]Qiao Lei,Deng Guantie.The Riesz decomposition theorem for superharmonic functions in a cone and its application(in Chinese)[J].Scientia Sinica(Math.),2012,42(8):763–774.

[16]Qiao Lei,Deng Guantie.Integral representation for the solution of the stationary Schrodinger equation in a cone[J].Math.Nachr.,2012,285(16):2029–2038.

[17]Qiao Lei,Deng GuanTie,Pan GuoShuang.Exceptional sets of modified Poisson integral and Green potential in the upper-half space[J].Scientia Sinica(Math.),2010,40(8):787–800.

[18]Reed M,Simon B.Methods of modern mathematical physics[M].Vol.3,London,New York,San Francisco:Acad.Press,1970.

[19]Rosenblum G V,Solomyak M Z,Shubin M A.Spectral theory of differential operators[M].Moscow: VINITI,1989.

[21]Stein E M.Singular integrals and differentiability properties of functions[M].New Jersey:Princeton University Press,1970.

[22]Verzhbinskii G M,Maz’ya V G.Asymptotic behavior of solutions of elliptic equations of the second order close to a boundary.I[J].Sibirsk.Matem.Zh.,1971,12(6):1217–1249.

[23]Zhang Yanhui,Deng Guantie.Growth properties of generalized Poisson integral in the half space[J]. J.Math.,2013,33(3):473–478.

錐中與穩(wěn)態(tài)的薛定諤算子相關(guān)的廣義Martin函數(shù)無窮遠(yuǎn)處的控制

龍品紅,韓惠麗

(寧夏大學(xué)數(shù)學(xué)計(jì)算機(jī)學(xué)院,寧夏銀川750021)

本文研究了穩(wěn)態(tài)的薛定諤算子的Dirichlet問題和Martin函數(shù)的邊界行為.利用廣義Martin表示和穩(wěn)態(tài)的薛定諤算子對應(yīng)的常微分方程基本解,在具有光滑邊界的錐形區(qū)域中獲得了與穩(wěn)態(tài)的薛定諤算子相關(guān)的廣義Martin函數(shù)無窮遠(yuǎn)處廣義調(diào)和控制的一些刻畫,推廣了拉普拉斯算子情形的結(jié)果.

穩(wěn)態(tài)的薛定諤算子;Martin函數(shù);調(diào)和控制;極細(xì);錐

O174.3

tion:31B05;31B25;31C35

A

0255-7797(2017)01-0051-12

?Received date:2014-11-22Accepted date:2015-02-11

Foundation item:Supported by National Natural Science Foundation of China(11271045; 11261041);Natural Science Foundation of Ningxia University(NDZR1301);Startup Foundation for Doctor Scientific Research of Ningxia University.

Biography:Long Pinhong(1978–),male,born at Chenzhou,Hunan,lecturer,major in complex analysis and potential theory.