GLOBAL EXISTENCE AND BLOW-UP OF SOLUTIONS FOR NEWTONIAN FILTRATION EQUATIONS COUPLED WITH BOUNDARY CONDITIONS
WANG Ze-jia,ZHOU Hai-hua,XU Jian-lei,WEN Kai
(College of Mathematics and Information Science,Jiangxi Normal University,Nanchang 330022,China )
GLOBAL EXISTENCE AND BLOW-UP OF SOLUTIONS FOR NEWTONIAN FILTRATION EQUATIONS COUPLED WITH BOUNDARY CONDITIONS
WANG Ze-jia,ZHOU Hai-hua,XU Jian-lei,WEN Kai
(College of Mathematics and Information Science,Jiangxi Normal University,Nanchang 330022,China )
In this paper,we deal with the large time behavior of solutions to the multidimensional Newtonian filtration equations coupled via the nonlinear boundary conditions.By constructing various kinds of upper and lower solutions,we obtain the critical global existence curve and the critical Fujita curve.
global existence;blow up;Newtonian filtration equation;critical curves
1 Introduction
In this paper,we deal with Newtonian filtration equations on the exterior domain of the unit ball in RN,i.e.,
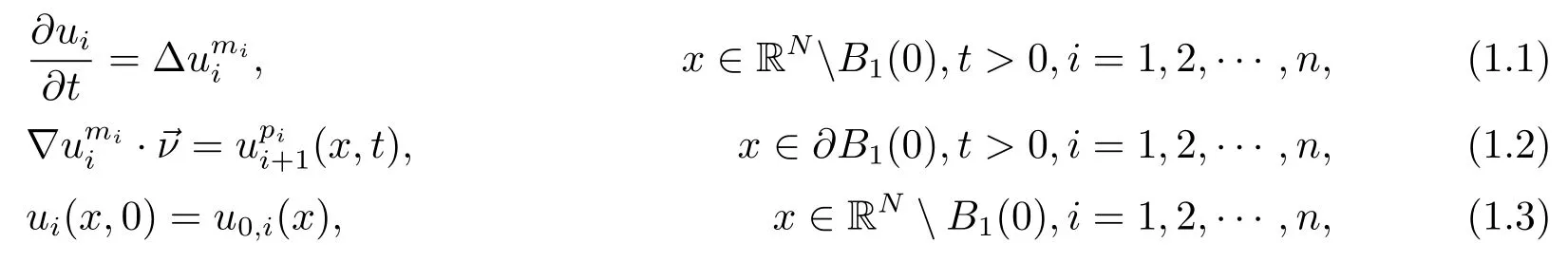
where mi>1,pi≥0,un+1=u1,B1(0)is the unit ball in RNwith boundary?B1(0),is the inward normal vector on?B1(0),and u0,i(x)are nonnegative,suitably smooth and bounded functions with compact support that satisfy the appropriate compatibility conditions.
The equation in(1.1)was intensively used in the models of chemical reactions,population dynamics,heat transfer,and so on.For problems(1.1)–(1.3),the local existence and the comparison principle of the weak solutions can be established,see[1,2].In this paper, we investigate the large time behavior of solutions to systems(1.1)–(1.3),such as global existence and blow-up in a finite time.
Since the beginning work on critical exponent done by Fujita[3]in 1966,lots of Fujita type results were established for various of problems,see the survey papers[4–6]and the references therein.It was Glalaktionov and Levine who first discussed the critical exponents for the one-dimensional nonlinear diffusion equations with boundary sources in[7]:
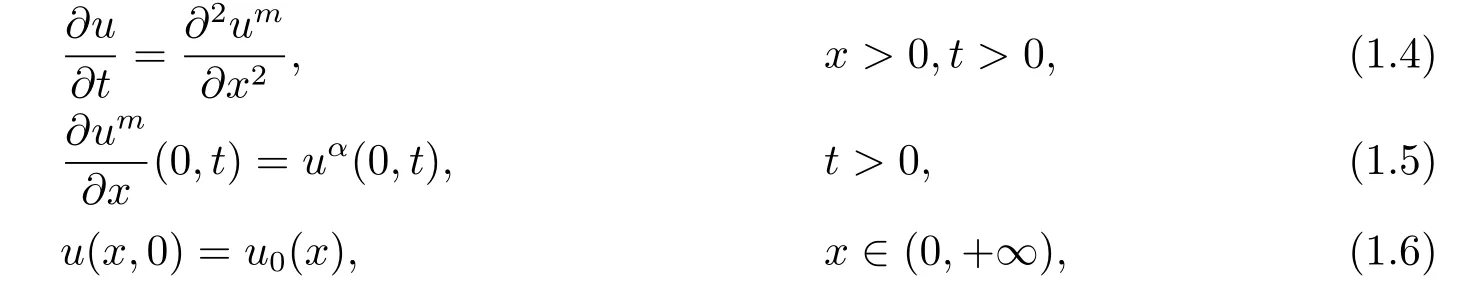
here m>1,α≥0.For problems(1.4)–(1.6),they proved that α0=(m+1)/2,αc=m+1. Here,we call α0as the critical global existence exponent and αcas the critical Fujita exponent respectively,
(i)if 0<α<α0,then every nontrivial nonnegative solution is global in time;
(ii)if α0<α<αc,then the nontrivial nonnegative solutions blow up in a finite time;
(iii)if α>αc,then the solutions exist globally for the small initial data and blow up in a finite time for the large initial data.
In fact,instead of critical exponents there exist the critical global existence curve and the critical Fujita curve for the coupled system of diffusion equations,see[8].For the one-dimensional nonlinear diffusion equations,Quirs and Rossi[9]considered the coupled Newtonian filtration equations as follows
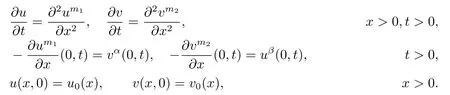
They showed that the critical global existence curve is given by αβ=(m1+1)(m2+1)/4 and the critical Fujita curve is given by min{α1+β1,α2+β2}=0,where
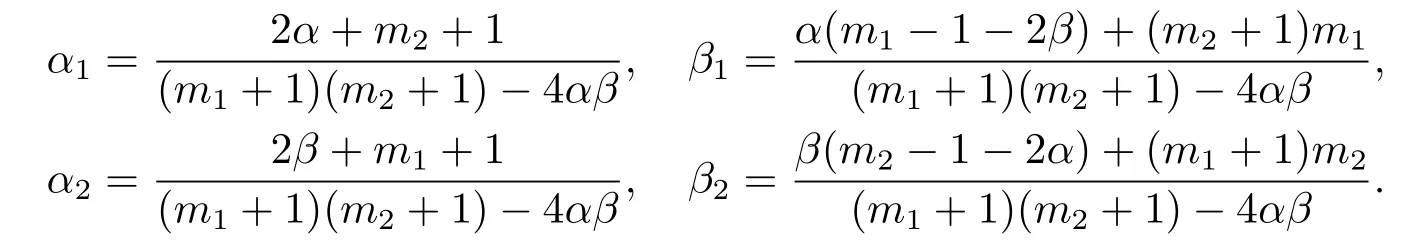
The similar results were established in[10–12].
In the present paper,we consider the critical curves for the multi-dimensional systems (1.1)–(1.3),the case of single equation was studied in[13]and proved that both the critical global existence exponent and the critical Fujita exponent are given by p=m.We extend the results in[13]to the problem on multiple equations.Furthermore,by virtue of the radial symmetry of the exterior domain of the unit ball,we can extend our results to the following more general equations

The rest of this paper is organized as follows.Section 2 is devoted to the large time behavior of solutions to the nonlinear boundary problem for the Newtonian filtration equations, namely,(1.1)–(1.3)and(1.7),(1.2),(1.3).
2 Main Results and Their Proofs
In this section,we first introduce our results on the system of Newtonian filtration equations coupled with boundary conditions,then we give the proofs.
Theorem 2.1The critical global existence curve and the critical Fujita curve for systems(1.1)–(1.3)are given by
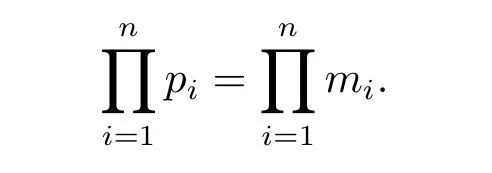
Theorem 2.2Assumei>2-N,N≥1.For equation(1.7)with the initial and boundary conditions(1.2),(1.3),the critical global existence curve and the critical Fujita curve both are given by
Before we give the proof of Theorem 2.1 and Theorem 2.2,we consider the problem
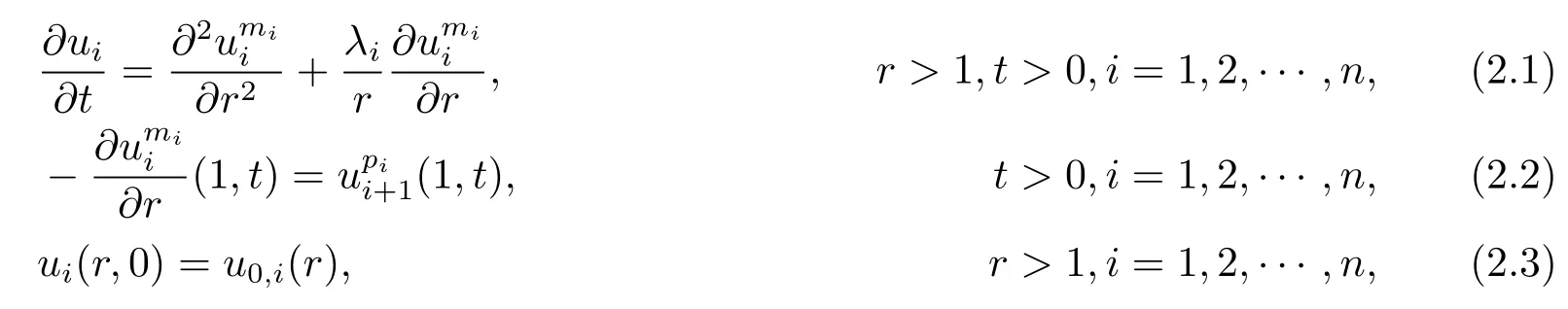
where r=|x|,mi>1,pi≥0,N≥1,λi>1,and u0,1(r),u0,2(r),···,u0,n(r)are nonnegative,nontrivial functions with compact supports.Clearly,the solution(u1,u2,···,un) of the system(2.1)–(2.3)with λi=N-1 is also the solution of systems(1.1)–(1.3)if u0,1(x),u0,2(x),···,u0,n(x)are radially symmetrical.If λi=i+N-1,the same facts also hold valid between systems(2.1)–(2.3)with systems(1.7),(1.2),(1.3).In order to obtain Theorem 2.1,Theorem 2.2,we firstly show the following results on systems(2.1)–(2.3).
Proposition 2.1Ifmi,then all nonnegative nontrivial solutions to systems(2.1)–(2.3)exist globally in time.
Proposition 2.2Ifmi,then the nonnegative solutions with large initial data to systems(2.1)–(2.3)blow up in a finite time.
Remark 1It can be seen from Proposition 2.1 and Proposition 2.2 that the critical global existence curve for systems(2.1)–(2.3)is
Proposition 2.3Ifmi,then every nonnegative nontrivial solution with small initial data to problems(2.1)–(2.3)exists globally.
Remark 2From Proposition 2.1–Proposition 2.3,we have the critical Fujita curve for systems(2.1)–(2.3)is given by
Now,we prove Proposition 2.1–Proposition 2.3.
Proof of Proposition 2.1.We prove this proposition by constructing a kind of global supersolution in the following form
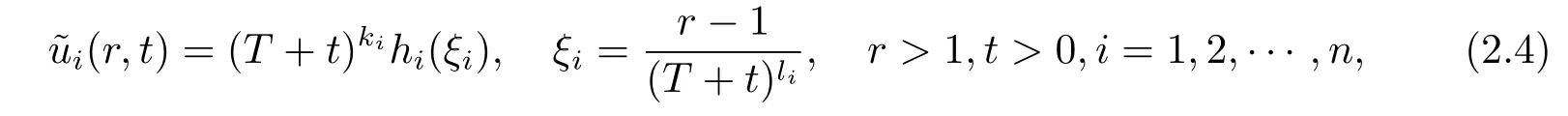
where T>0,and mn+1=m1,ki+1=kiγi=k1,i=1,2,···,n-1 with k1being the positive constants to be determined and
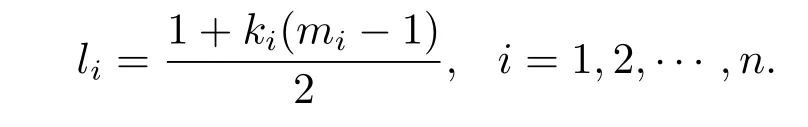
Fix ξi>0 for any i∈{1,2,···,n},we take
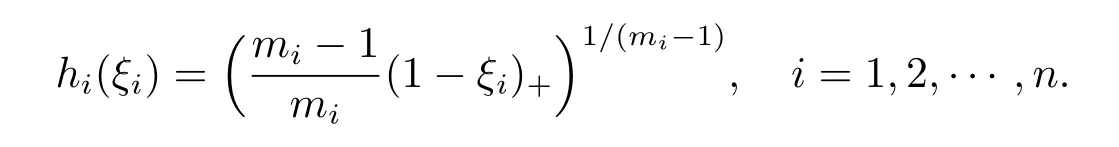
Denote
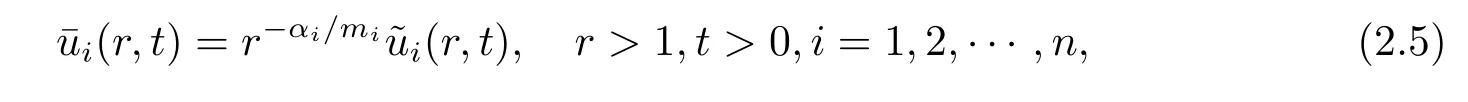
where αiare given by the following
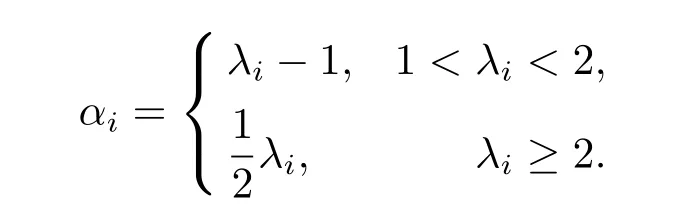
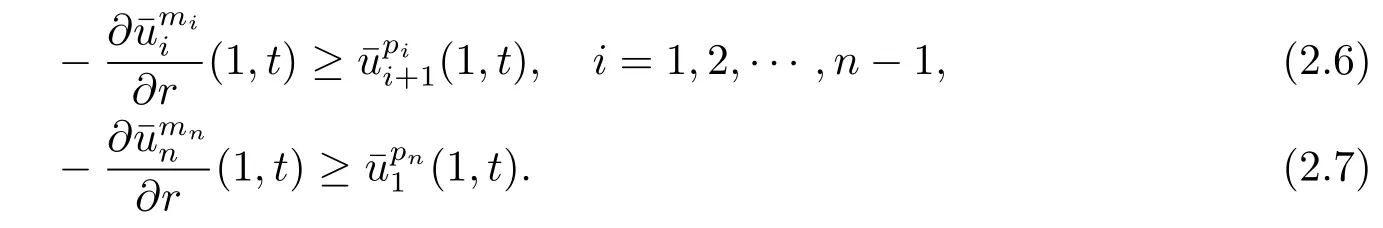
Hence,due to that
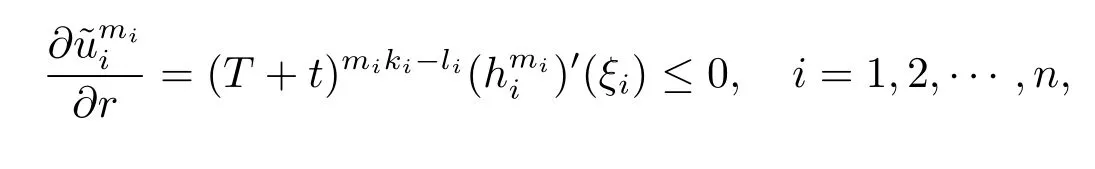
we have
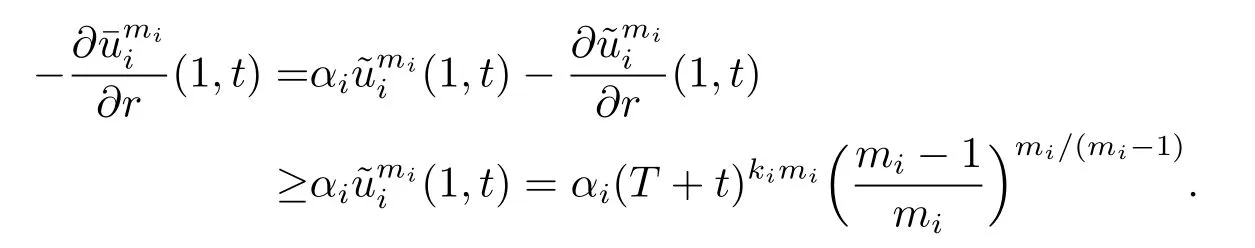
Similarly,it is clear that
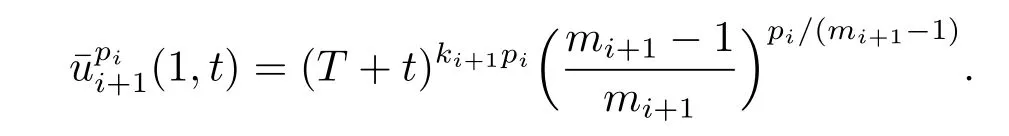
Thus,the inequalities in(2.6)and(2.7)are valid if
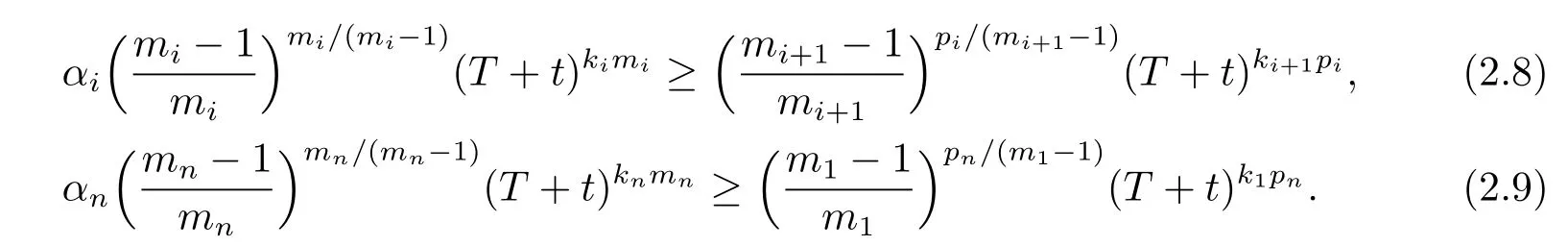
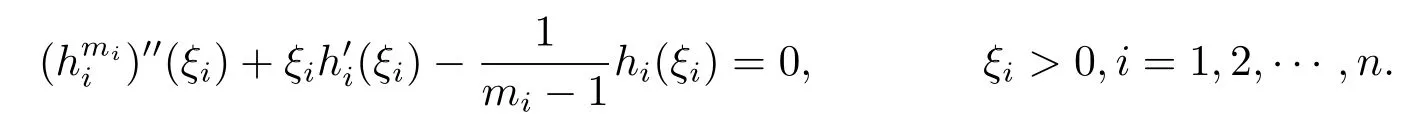
Then
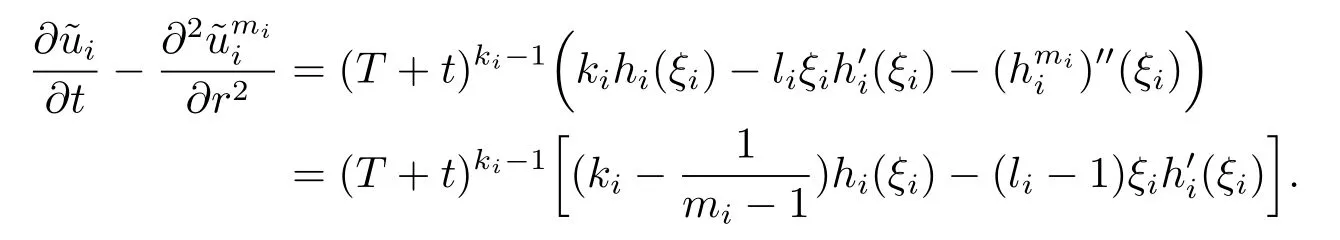
Recall that ki+1=kiγi=γj,i=1,2,···,n-1,we choose k1>0 such that
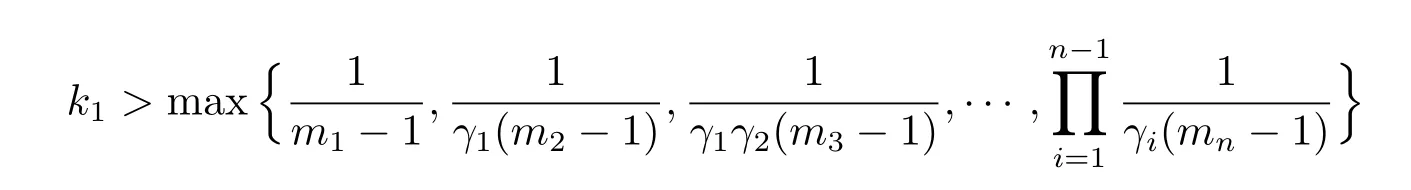
implies li>1,ki>.Combing with that≤0,we get
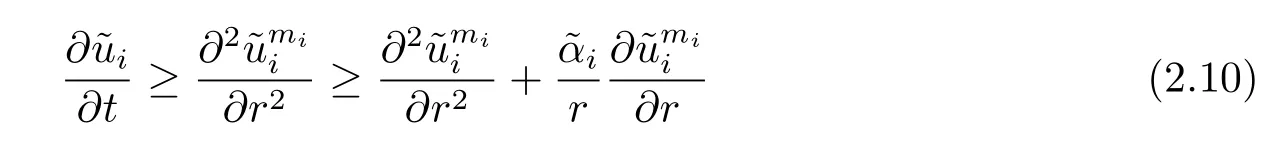
with
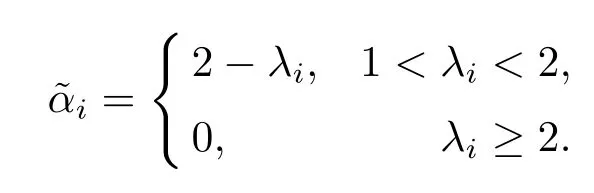
Note that
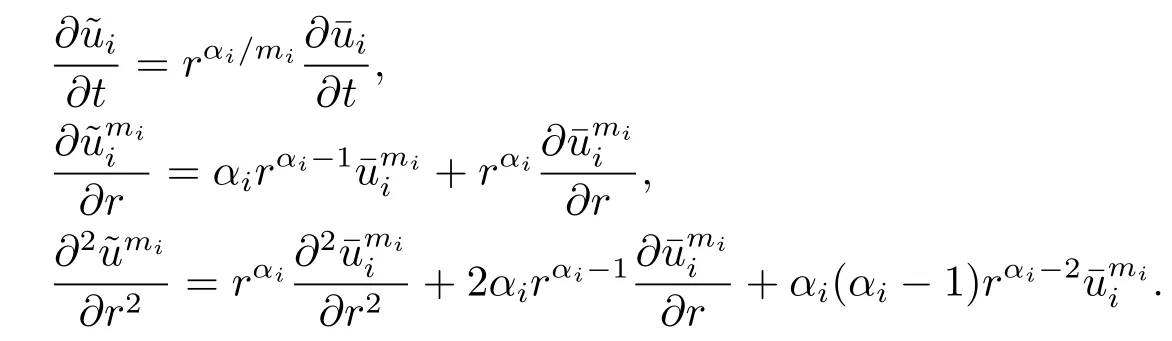
Substituting the above equalities into(2.10),we obtain that
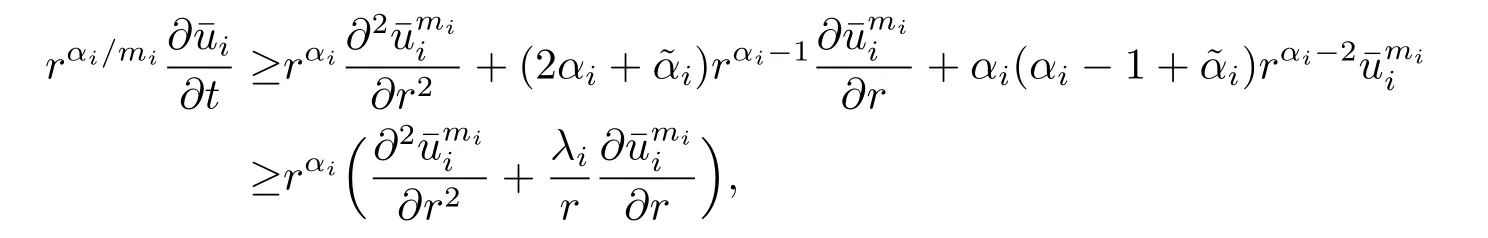
due to that αi-1+i≥0 and 2αi+i=λi.The above inequality implies that for r>1,
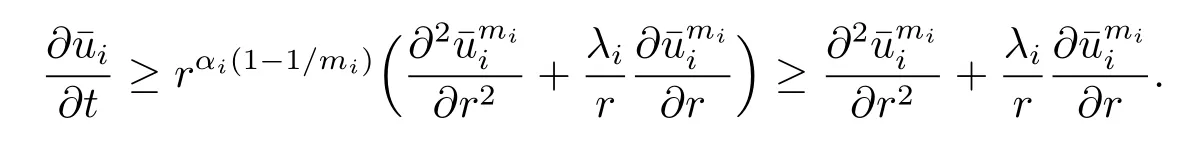
Finally,we verify the initial conditions that
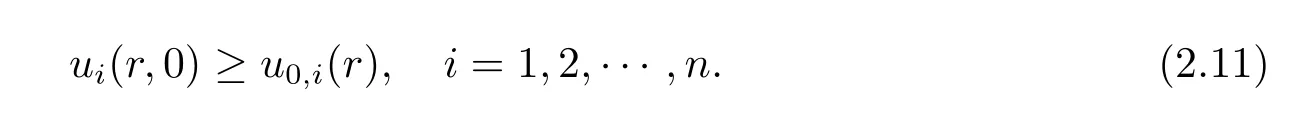
Denote
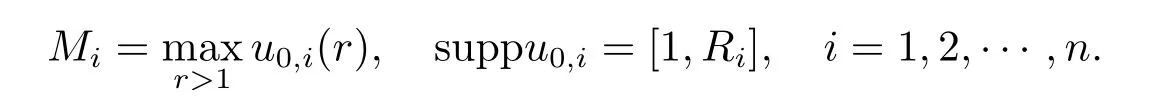
Then(2.11)holds provided with
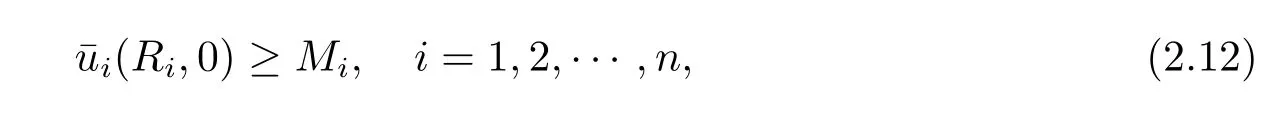
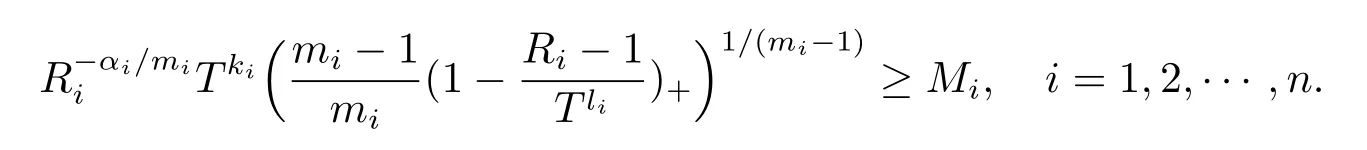
From the above,for large T satisfying(2.8)and(2.12),it is seen thatis a supersolution of systems(2.1)–(2.3).Therefore,we have the solution of problems(2.1)–(2.3) exists globally by the comparison principle.The proof is completed.
Proof of Proposition 2.2The proposition is proved by constructing a kind of lower blow-up lower solution of systems(2.1)–(2.3).For r>1,0<t<T,set
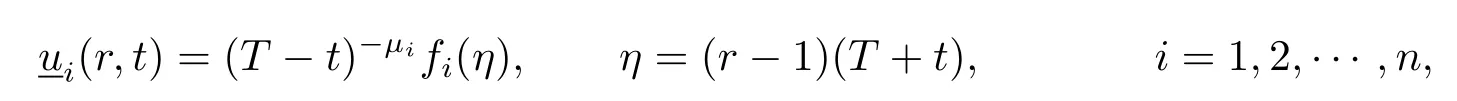
where T>0,μ1>0 is a given constant,
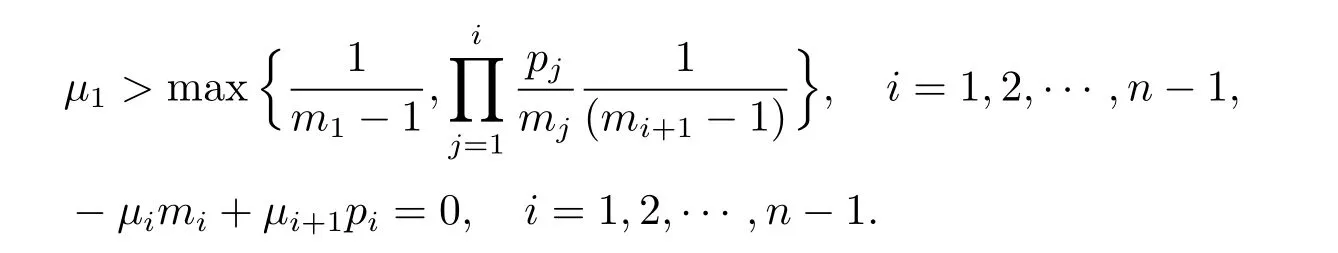
Assume that fisatisfy≥0,i=1,2,···,n,by a direct calculation,we can see thatis a subsolution to systems(2.1)–(2.3),if the following inequalities hold

Note that r>1 and
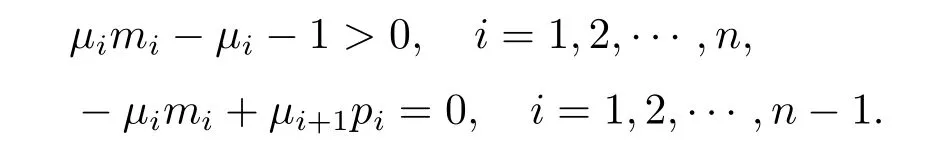
Thus(2.13)and(2.14)hold if

with fn+1=f1.For any i∈{1,2,···,n},namely,
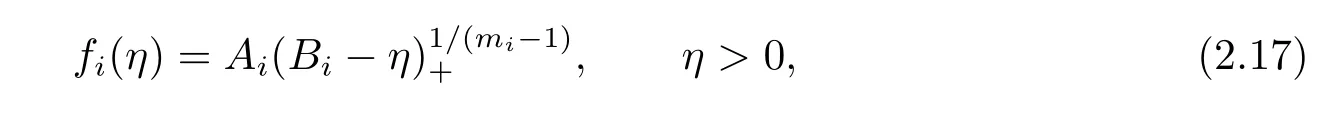
where Aiare positive constants to be determined,and
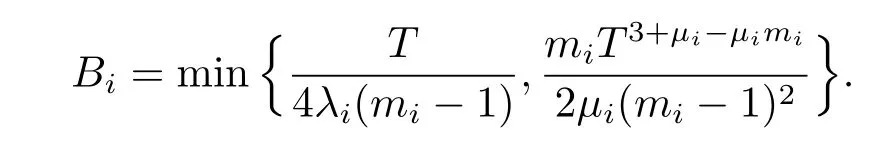
In the following,we verify that the above fisatisfy(2.15)and(2.16).Substituting(2.17) into(2.15)yields that
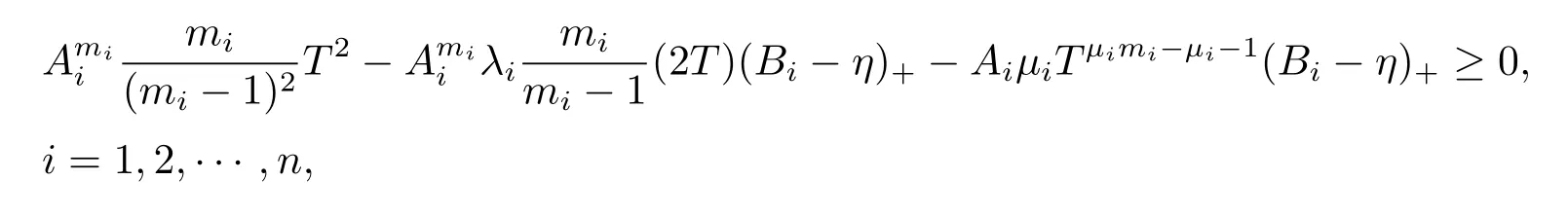
which can be obtained by the following
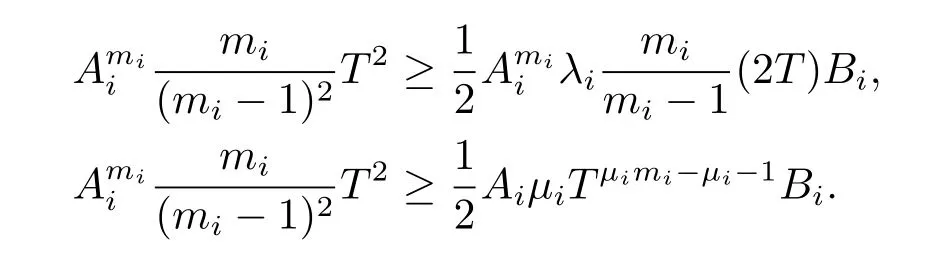
The choice of Bimakes us to conclude that the above inequalities hold for Ai>1.This indicated that fisatisfy(2.15).
Next,substitute(2.17)into(2.16),we have
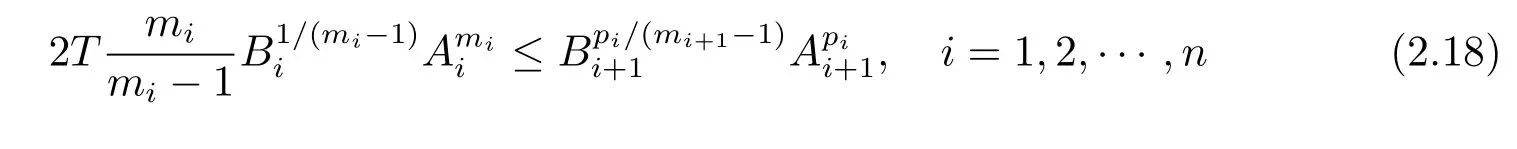
with An+1=A1.Sincemi,there exists a constant k>1,such that

For i∈{1,2,···,n-1},set Ai+1=.Then(2.18)can also be written as
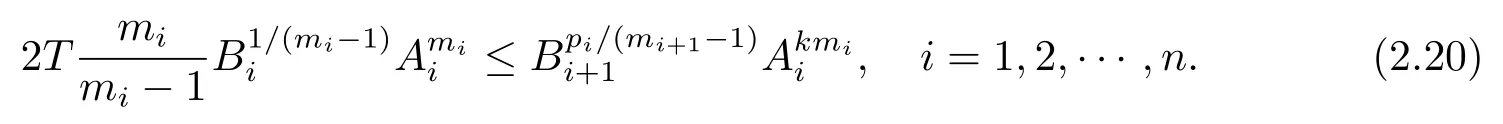
Choose Ailarge enough to satisfy(2.20),then we get(2.16).
Therefore,the solution(u1,u2,···,un)with(r,0)(i=1,2,···,n)of problems(2.1)–(2.3)blows up in a finite time.The proof is completed.
Proof of Proposition 2.3The proof is completed by constructing the following global upper solution
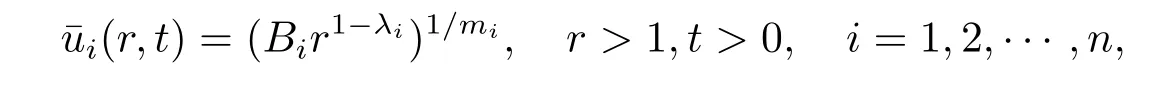
where
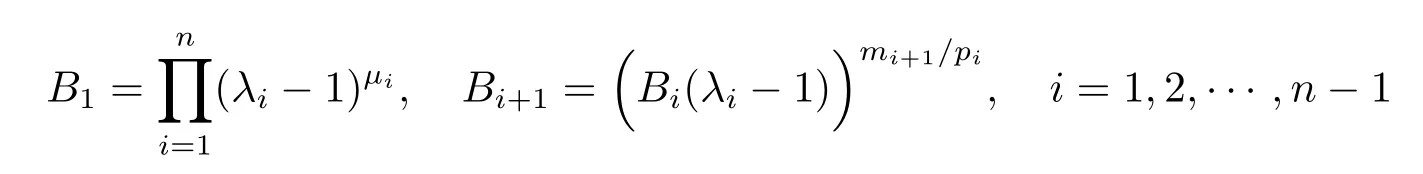
withμi=.It can easily be checked that
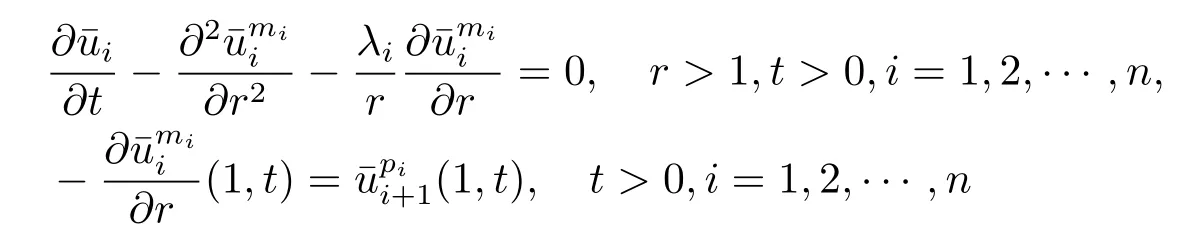
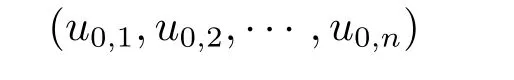
is small enough that
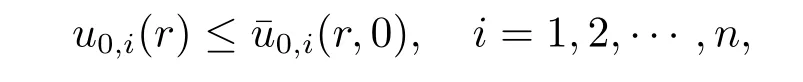
the solutions of problems(2.1)–(2.3)exist globally in time.
Now,we prove the main result for systems(1.1)–(1.3),i.e.,Theorem 2.1.
Proof of Theorem 2.1Noticing that the functions u0,1(x),u0,2(x),···,u0,n(x)have compact supports,we can choose n bounded,radially symmetrical functions,denoted by ui(x)=ui(|x|)≥u0,i(x),i=1,2,···,n.By using Proposition 2.1 and the comparison principle,we can obtain the global existence of solutions for systems(1.1)–(1.3).However,forthe large and radially symmetric functions(|x|,0),···,defined in the proof of Proposition 2.2,if(u0,1,u0,2,···,u0,n)is large enough such that u0,i(x)≥i=1,2,···,n,then the solutions of systems(1.1)–(1.3)withmiblow up by the comparison principle and Proposition 2.2.This clarifies that the critical global existence curve ismifor system(1.1)–(1.3).
On the other hand,using the comparison principle again,we conclude that the solution (u1,u2,···,un)of(1.1)–(1.3)with
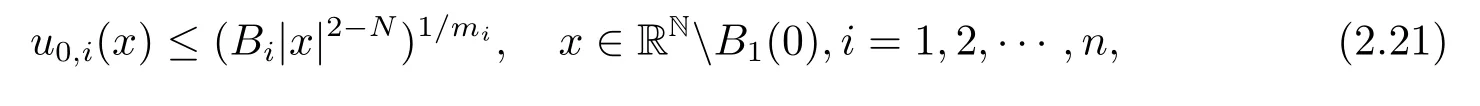
where

withμi=,exists globally formiby Proposition 2.3.This combined with Proposition 2.2 indicates that the critical Fujita curvemifor systems (1.1)–(1.3).
Proof of Theorem 2.2By virtue of the same discussion in the proof of Theorem 2.1, if we prove this theorem by takingin systems(2.1)–(2.3),and replacing (2.21)with
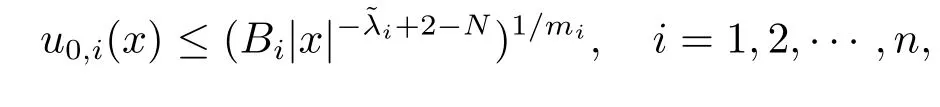
where
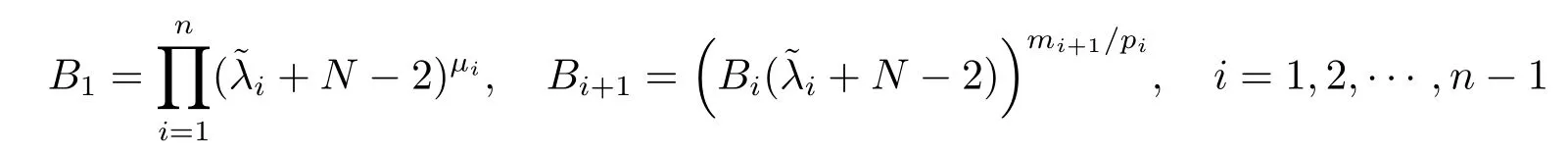
withμi=.The proof is completed.
[1]Kalashnikov A S.Some problems of the qualitative theory of nonlinear degenerate second-order parabolic equations[J].Russian Math.Surveys,1987,42(2):169–222.
[2]Wu Z Q,Zhao J N,Yin J X,Li H L.Nonlinear diffusion equations[M].Singapore:World Scientific Publishing Co.,2001.
[3]Fujita H.On the blowing up of solutions of the Cauchy problem for ut=Δu+u1+α[J].J.Fac.Sci. Univ.Tokyo Sect.I,1966,13:109–124.
[4]Deng K,Levine H A.The role of critical exponents in blow-up theorems:the sequel[J].J.Math. Anal.Appl.,2000,243(1):85–126.
[5]Li M,Xie C H.Global existence and blow-up of solutions for degenerate parabolic systems[J].J. Math.,2004,24(2):197–203.
[6]Galaktionov V A,Levine H A.A general approach to critical Fujita exponents in nonlinear parabolic problems[J].Nonl.Anal.,1998,34(7):1005–1027.
[7]Galaktionov V A,Levine H A.On critical Fujita exponents for heat equations with nonlinear flux conditions on the boundary[J].Israel J.Math.,1996,94(1):125–146.
[8]Deng K,Fila M,Levine H A.On critical exponents for a system of heat equations coupled in the boundary conditions[J].Acta Mathematica Universitatis Comenianae,New Series,1994,63(2): 169–192.
[10]Mi Y S,Mu C L,Zhou S M.A degenerate and singular parabolic system coupled through boundary conditions[J].Bull.Malays.Math.Sci.Soc.,2013,36(1):229–241.
[11]Wang Z J,Zhou Q,Lou W Q.Critical exponents for porous medium systems coupled via nonlinear boundary flux[J].Nonl.Anal.TMA,2009,71(5-6):2134–2140.
[12]Zheng S N,Song X F,Jiang Z X.Critical Fujita exponents for degenerate parabolic equations coupled via nonlinear boundary flux[J].J.Math.Anal.Appl.,2004,298:308–324.
[13]Wang Z J,Yin J X,Wang C P,Gao H.Large time behavior of solutions to Newtonian filtralion equation with nonlinear boundary sources[J].J.Evol.Equ.,2007,7(4):615–648.
邊界耦合的牛頓滲流方程組解的整體存在與爆破
王澤佳,周海花,徐劍磊,溫凱
(江西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,江西南昌330022)
本文研究了由邊界條件耦合的多維牛頓滲流方程組解的長(zhǎng)時(shí)間行為.利用構(gòu)造的多種上下解,得到了整體存在臨界曲線與Fujita臨界曲線.
整體存在;爆破;牛頓滲流方程;臨界曲線
O175.26
tion:35K65;35B33
A
0255-7797(2017)01-0011-10
?Received date:2014-08-08Accepted date:2015-04-07
Foundation item:Supported by National Natural Science Foundation of China(11361029), Jiangxi Province Planning Project of Science and Technology(GJJ14270)and National Natural Science Foundation of Jiangxi Province(20142BAB211001).
Biography:Wang Zejia(1979–),female,born at Anda,Heilongjiang,professor,major in partial differential equations.

