付麗,閆盼盼,曹重光

(1.綏化學(xué)院信息工程學(xué)院,黑龍江 綏化 152061;2.黑龍江大學(xué)數(shù)學(xué)科學(xué)學(xué)院,黑龍江 哈爾濱 150080)

關(guān)于域上上三角矩陣的誘導(dǎo)映射

付麗1,閆盼盼2,曹重光2

(1.綏化學(xué)院信息工程學(xué)院,黑龍江 綏化 152061;2.黑龍江大學(xué)數(shù)學(xué)科學(xué)學(xué)院,黑龍江 哈爾濱 150080)

令F是一個域,Tn(F)是F上所有n×n上三角矩陣的集合.本文分別給出了矩陣保相似性及保交換性的定義,并使用矩陣技術(shù)和初等方法,得到了Tn(F)的保相似性及保交換性的誘導(dǎo)映射的一般形式,并且給出了例子,來解釋一些結(jié)果之間的關(guān)系.

上三角矩陣;保相似性;保交換性;誘導(dǎo)映射

1 引言

近年來刻畫矩陣集合保持某些性質(zhì)的映射的研究更感興趣于映射沒有線性和加法假定的情形,例如文獻(xiàn)[1-5].本文研究的誘導(dǎo)映射,其實也是這類問題的一種,如文獻(xiàn)[6-7].

設(shè)F是一個域,Mn(F)及Tn(F)分別記F上所有n階矩陣及所有n階上三角陣的集合.設(shè)f是Mn(F)(Tn(F))到自身的映射,fij是F上的函數(shù),其中ij∈{1,2,···,n}.如果定義

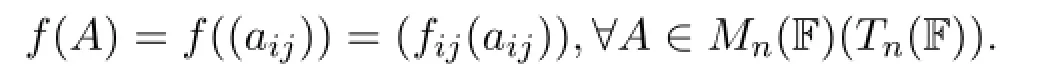
則稱f是由{fij}誘導(dǎo)的映射.簡稱Mn(F)(Tn(F))的誘導(dǎo)映射.

如果A與B相似,能推出f(A)與f(B)相似,則稱f保相似性.如果AB=BA,能推出f(A)f(B)=f(B)f(A),則稱f保交換性.本文分別刻畫域上上三角矩陣保相似性及保交換性的誘導(dǎo)映射.

在本文中用F?記F中所有非0元的集合,Eij表示(i,j)位置是1,其余位置是零的矩陣,In記n階單位陣.記[1,n]表示集合{1,2,···,n}.

2 保相似性的誘導(dǎo)映射

定義2.1對A,B∈Tn(F),若存在可逆矩陣P∈Mn(F),使得A=PBP-1,則稱A相似于B,記作A～B.

引理 2.2[7]設(shè)F為一個域,n≥2是整數(shù),若A∈Tn(F),滿足A2=0,rankA=r,那么存在一個可逆矩陣P∈Mn(F),使得

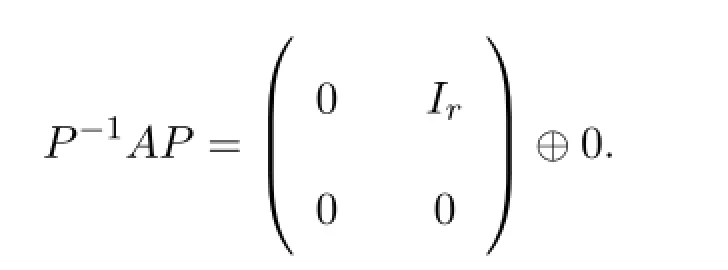
定理2.3設(shè)F為一個域,n≥3是整數(shù),f為Tn(F)到自身的誘導(dǎo)映射,且滿足f(0)=0,則對任意A=(aij)∈Tn(F),f保相似性的充分必要條件是f為下列形式之一：

(1)存在F上一個函數(shù)φ,使得φ=f11=···=fnn且f(A)=diag(φ(a11),···,φ(ann));

(2)存在一個可逆對角陣P∈Tn(F),q∈F?和F上一個單射自同態(tài)δ,使得

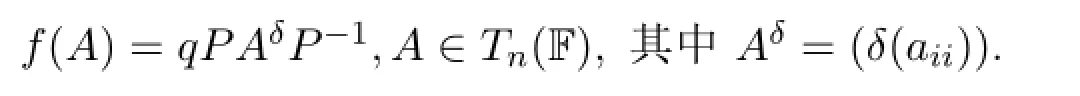
3 保交換性的誘導(dǎo)映射

在Tn(F)的誘導(dǎo)映射的定義中涉及n-1個函數(shù)f12,f23,···,fn-1,n,對這些函數(shù)可定義如下的類集合

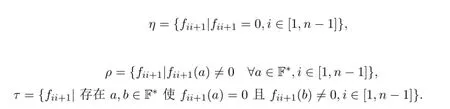
將函數(shù)f12,f23,···,fn-1,n所屬的類集合,從左到右依次寫成一個序列,稱為誘導(dǎo)映射f的類序列.例如ητρρητ為n=7時f的類序列,它說明f12∈η,f23∈τ,f34∈ρ,f45∈ρ,f56∈η, f67∈τ.如果在f(0)=0的條件下,f是Tn(F)的保交換的誘導(dǎo)映射,我們有如下結(jié)果.

引理3.1設(shè)n≥3是整數(shù),f(0)=0,其中f是Tn(F)的保交換的誘導(dǎo)映射,且對任意的i∈[1,n]有fii(1)0,則在f的類序列中不會出現(xiàn)相鄰兩類為ρτ,τρ,ττ這三種情況.

定理3.2設(shè)f為Tn(F)的誘導(dǎo)映射,f(0)=0,n≥3是一個整數(shù),且滿足則f保交換當(dāng)且僅當(dāng)

定理 3.3F是一個域,f1為Tm(F)的誘導(dǎo)映射,f1(0)=0,且滿足fii(1)≠0,(i∈[1,n])

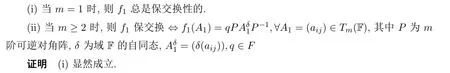
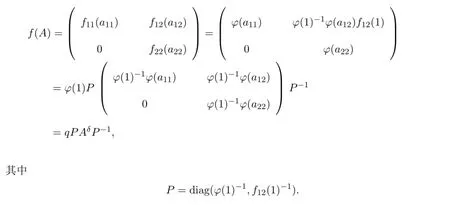
[1]Huang L.P..Geometry of Matrices over Ring[M].Beijing：Science Press,2006.

[2]Cao C.G.,Ge Y.L.and Yao H.M..Maps preserving classical adjoint of products of two matrices[J].Linear and Multilinear Algebra,2013,61(12)：1593-1604.

[3]P.?emrl,Commutativity preserving maps[J],Linear Algebra Appl,2008,429(1)：1051-1070.

[4]You H.,Wang Z.Y..k-Potence preserving maps without the Linearty and surjectivity assumptions[J].Linear Algebra Appl,2007,426：238-254.

[5]Chooi W.L.and Ng W.S..On classical adjoint-commuting mappings between matrix algebras[J].Linear Algebra Appl,2010,432：2589-2599.

[6]Liu S.W.and Zhang G.D..Maps preserving rank 1 matrices over fields[J].Journal of Natural Science of Heilongjiang University,2006,23(1)：138-140.

[7]YYang L.,Ben X.Z.,Zhang M.and Cao C.G..Induced Maps on matrices over fields[J].Abstract and Applied Analysis,vol.2014,Article ID 596796,5 pages,2014

Induced maps on upper triangular matrices over fields

Fu Li1,Yan Panpan2,Cao Chongguang2
(1.School of Information Engineering,Suihua University,Suihua 152061,China; 2.School of Mathematical Science,Heilongjiang University,Harbin 150080,China)

Let F is a field and Tn(F)is a set of all n×n upper triangular matrices over F.In this paper the definition of preserving similarity and commutativity about matvix are given respectively.This paper gets the general forms of induced maps about preserving similarity and commutativity by using the techniques of matrix and elementary method and explain the relationship between the results through examples.

upper triangular tatrix,preserving similarity,preserving commutativity,induced map

O151.21

A

1008-5513(2016)06-0630-10

10.3969/j.issn.1008-5513.2016.06.010

2016-09-09.

國家自然科學(xué)基金(11371109);綏化學(xué)院2015年科學(xué)技術(shù)研究項目(K1502004).

付麗(1982-),碩士生,講師,研究方向：矩陣代數(shù).

2010 MSC:15A04