劉麗亞,谷峰

(杭州師范大學(xué)數(shù)學(xué)系,浙江 杭州 310036)

b-度量空間中壓縮型映象的公共不動(dòng)點(diǎn)定理

劉麗亞,谷峰

(杭州師范大學(xué)數(shù)學(xué)系,浙江 杭州 310036)

在完備的b-空間中,建立一個(gè)壓縮型映象,研究公共不動(dòng)點(diǎn)的存在性和唯一性,得到了一個(gè)新的公共不動(dòng)點(diǎn)定理.舉例證明了在b-空間中的新結(jié)果,改進(jìn)了當(dāng)前文獻(xiàn)中的結(jié)果.

完備b-空間;壓縮映象;公共不動(dòng)點(diǎn);弱相容

1 引言和預(yù)備知識(shí)

Czerwik在文獻(xiàn)[1-2]中介紹了b-度量空間的概念,最近,文獻(xiàn)[3-13]在b-度量空間中研究了滿足一定壓縮條件的非線性算子的不動(dòng)點(diǎn)的存在性問題,得到了一些新結(jié)果.

受上述文獻(xiàn)的啟發(fā),本文介紹b-度量空間的定義,主要在完備b-度量空間中研究壓縮型映射不動(dòng)點(diǎn)存在性問題,得到了幾個(gè)新的不動(dòng)點(diǎn)定理,本文的結(jié)果推廣了一些已知的相關(guān)結(jié)果,而且也是度量空間中某些經(jīng)典結(jié)果在b-度量空間的進(jìn)一步推廣.在介紹主要結(jié)果之前,先介紹一些基本概念和已知結(jié)果.

定義1.1[1]設(shè)X是一非空集,令d：X×X→R+滿足：

(b-1)d(x,y)=0,若x=y;

(b-2)d(x,y)=d(y,x),?x,y∈X且x≠y;

(b-3)d(x,y)≤s(d(x,z)+d(z,y)),?x,y,z∈X,s≥1.

則稱函數(shù)d是X上的一個(gè)b-度量,或稱d是X上的一個(gè)b-度量,稱(X,d)為b-度量空間,s為其系數(shù).

定義1.2[8]設(shè)X是一非空集,(X,d)是b-度量空間,點(diǎn)列{xn}?X.

引理1.1[8]設(shè)X是一非空集,(X,d)是具有參數(shù)s≥1的b-度量空間,序列{xn},{yn}?X分別收斂于X中的兩點(diǎn)x,y,則有

特別的,當(dāng)x=y時(shí),有l(wèi)imn→∞d(xn,yn)=0.此外,?z∈X,有

引理1.2[8]設(shè)(X,d)是一個(gè)b-度量空間,序列{xn},{yn}?X,如果

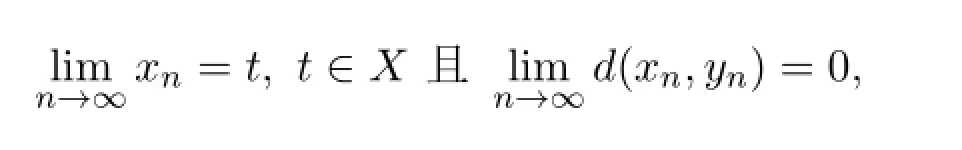
則

注 1.1[14]設(shè)X是一非空集,(X,d)是b-度量空間.在X中存在三個(gè)偏序關(guān)系和令A(yù),B,C,D,E,F：X→X是X中的六個(gè)自映象.

其中x∈X.

定義1.3[14]設(shè)X是一非空集,(X,d)是b-度量空間,是X上的一偏序關(guān)系.序列{xn},{yn}?X分別收斂于X中的兩點(diǎn)x,y,即

定義1.4[14]設(shè)是定義在b-度量空間(X,d)中的兩個(gè)偏序關(guān)系.令A(yù),B,C,D,f,g：X→X是X中的六個(gè)自映象.稱f是(A,B,C,D,g?1,?2)穩(wěn)定的,如果滿足下列條件：

定義1.5[13]b-度量空間(X,d)中的自映象對(duì)(f,g)稱為是弱相容的,若fx=gx,x∈X,就有fgx=gfx,即d(fx,gx)=0?d(fgx,gfx)=0.

2 主要內(nèi)容

該文處處假設(shè)以下兩種類型的函數(shù)：

定理2.1設(shè)X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的三個(gè)偏序關(guān)系.函數(shù)f,g,S,T,A,B,C,D,E,F,I：X→X為X上的11個(gè)的自映象,其中I表示X中的恒等映象,且滿足以下條件：

定理2.2設(shè)X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的三個(gè)偏序關(guān)系.函數(shù)f,g,S,T,A,B,C,D,E,F,I：X→X為X上的11個(gè)自映象,其中I表示X中的恒等映象,且滿足以下條件：

如果f,g,S和T其中之一在(X,d)上是閉區(qū)間,則當(dāng)(f,S)和 (g,T)是弱相容時(shí),這時(shí)f,g,S,T有唯一的公共不動(dòng)點(diǎn).

證明與定理2.1的證明方法類似,同理也可證得.

定義2.1[14]設(shè)X是一非空集,(X,d)是b-度量空間,其中是定義在X上的兩個(gè)偏序關(guān)系.令A(yù),B,C,D,f：X→X是X中的5個(gè)自映象.稱g是 (A,B,C,D,f)穩(wěn)定的,如果滿足下列條件：

注 2.1在定理2.1中,令函數(shù)S,T為X中的恒等映像I.即可得到以下結(jié)果.

推論2.1設(shè)X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的三個(gè)偏序關(guān)系.函數(shù)f,g,A,B,C,D,E,F,I：X→X為X上的9個(gè)自映象,其中I表示X中的恒等映象,且滿足以下條件：

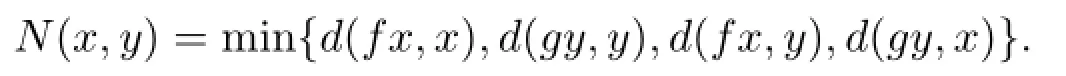
如果f和g其中之一在(X,d)中是閉區(qū)間,則f,g有唯一的公共不動(dòng)點(diǎn).

注 2.2[5]在推論2.1中,令函數(shù)f,g為X中的同一個(gè)映像T,即可得到以下結(jié)果.

推論 2.2設(shè)X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的兩個(gè)偏序關(guān)系.函數(shù)T,A,B,C,D：X→X為X上的五個(gè)自映象,且滿足以下條件：

3 非線性方程解的唯一性

令推論2.1中的A,B,C,D,E,FI為X中的恒等映象,定義偏序關(guān)系

在以上情形中,我們可以考慮方程組的解的存在性情況.

規(guī)定X=C[0,T]為所有[0,T]上的連續(xù)函數(shù)全體,現(xiàn)在我們考慮下列積分方程組在[0,T]中解的存在情況.

這里函數(shù)G1,G2：[0,T]×[0,T]×X→R+.

在X中定義b-度量為

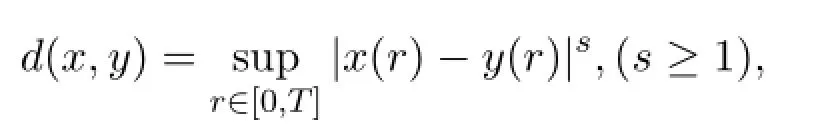
其中2s-1為其系數(shù).

假設(shè)在b-度量空間(X,d)中滿足以下條件：

定理3.1在條件(a)-(c)下,可證得方程(32)在X中存在唯一解.

[1]Czerwik S.Contraction mappings in b-metric spaces[J].Acta Math.Inform.Univ.Ostrav.1993,1,5-11.

[2]Czerwik S.Nonlinear set-valued contraction mappings in b-metric spaces[J].Atti.Sem.Math.Fis.Univ.Modena.,1998,46(2)：263-276.

[3]Aghajani A,Abbas M,Roshan JR.Common fixed point of generalized weak contractive mappings in partially ordered b-metric spaces[J].Math.Slovaca,2014,4：941-960.

[4]Akkouchi M.Common fixed point theorems for two self mappings of a b-metric space under an implicit relation[J].Hacet.J.Math.Stat.,2011,40(6)：805-810.

[5]Bota M F,Karapinar E,Mlesnite O.Ulam-Hyers stability results for fixed point problems via φ-ψcontractive mapping in b-metric space[J].Abstr.Appl.Anal.,2013,Article ID 825293.

[6]Bota M F,Karapinar E.A note on Some results on multi-valued weakly Jungck mappings in b-metric space[J].Cent.Eur.J.Math.,2013,11：1711-1712.

[7]Aydi H,Bota M F,Karapinar E,et al.A common fixed point for weak φ-contractions on b-metric spaces[J].Fixed Point Theory 2012,13(2)：337-346.

[8]Boriceanu M,Bota M,Petrusel A.Multi-valued fractals in b-metric spaces[J].Cent.Eur.J.Math., 2010,8(2)：367-377.

[9]Aydi H,Bota M,Karapinar E,et al.A common fixed point for weak φ-contractions on b-metric spaces[J].Fixed Point Theory,2012,13(2)：337-346.

[10]Bota M.Molnar A,Varga C.On Ekeland’s variational principle in b-metric spaces[J].Fixed Point Theory, 2011,12(2)：21-28.

[11]Boriceanu M.Strict fixed point theorems for multi-valued operators in b-metric spaces[J].International Journal of Modern Mathematics,2009,4(3)：285-301.

[12]Aghajani A,Abbas M,Roshan J R.Common fixed point of generalized weak contractive mappings in partially ordered b-metric spaces[J].Math.,2012,64(1)：941-960.

[13]Roshan J R,Shobkolaei N,Sedghi S,et al.Common fixed point of four maps in b-metric spaces[J].Hacettepe Journal of Mathematics and Statistics,2014,43(4)：613-624.

[14]Jleli,Samet.A fixed point problem under two constraint inequalities[J].Fixed Point Theory and Applications,2016,2016(1)：1-14.

A common fixed point theorem of contractive mappings in b-metric spaces

Liu Liya,Gu Feng
(Department of Mathematics,Hangzhou Norm University,Hangzhou 310036,China)

In complete b-metric spaces,by establishing a new contractive condition,we obtain the existence and the uniqueness of fixed point theorem,We also provide illustrative examples in support of our new results in b-metric spaces.The result obtained in this paper differ from the recent relative results in the literature.

complete b-metric space,contractive mappings,common fixed point,weak compatible

O178

A

1008-5513(2016)06-0591-15

10.3969/j.issn.1008-5513.2016.06.005

2016-09-01.

國家自然科學(xué)基金(11071169);浙江省自然科學(xué)基金(Y6110287).

劉麗亞(1990-),碩士生,研究方向：應(yīng)用非線性分析.

谷峰(1960-),教授,研究方向：應(yīng)用非線性分析.

2010 MSC:47H10,54H25