包立平

(杭州電子科技大學(xué)理學(xué)院,浙江杭州310018)

一類(lèi)奇攝動(dòng)半線性時(shí)滯拋物型偏微分方程的漸近解

包立平

(杭州電子科技大學(xué)理學(xué)院,浙江杭州310018)

文中討論了一類(lèi)奇攝動(dòng)時(shí)滯拋物型偏微分方程的初邊值問(wèn)題,得到了其形式漸近展開(kāi),證明了奇攝動(dòng)半線性時(shí)滯偏微分方程的極大值原理,從而得到了最大值估計(jì)及相應(yīng)的Schuader估計(jì).在此基礎(chǔ)上,得到了柱狀區(qū)域上解的存在唯一性和漸近解的一致有效性.

奇攝動(dòng);半線性;時(shí)滯拋物型方程;漸近展開(kāi);Schuader估計(jì);最大值原理;余項(xiàng)估計(jì)

§1 引 言

奇攝動(dòng)時(shí)滯拋物型偏微分方程在各種學(xué)科的研究中得到了很大的應(yīng)用.例如在種群動(dòng)力學(xué),傳染病學(xué)等方面有重要應(yīng)用;在隨機(jī)微分方程的研究中也有重要價(jià)值.

近年來(lái)奇攝動(dòng)時(shí)滯拋物型偏微分方程的研究得到了人們的重視,如A.R.Ansari,S.A.Bakr,G.I.Shishkin[1]研究了一類(lèi)奇攝動(dòng)時(shí)滯線性拋物型偏微分方程問(wèn)題,得到了矩形域上的解的存在唯一性和一致有效漸近解.莫嘉琪[2]得到了小時(shí)滯的奇攝動(dòng)拋物型偏微分方程的一致有效漸近解等.

本文研究如下一類(lèi)奇攝動(dòng)時(shí)滯拋物型偏微分方程的初邊值問(wèn)題

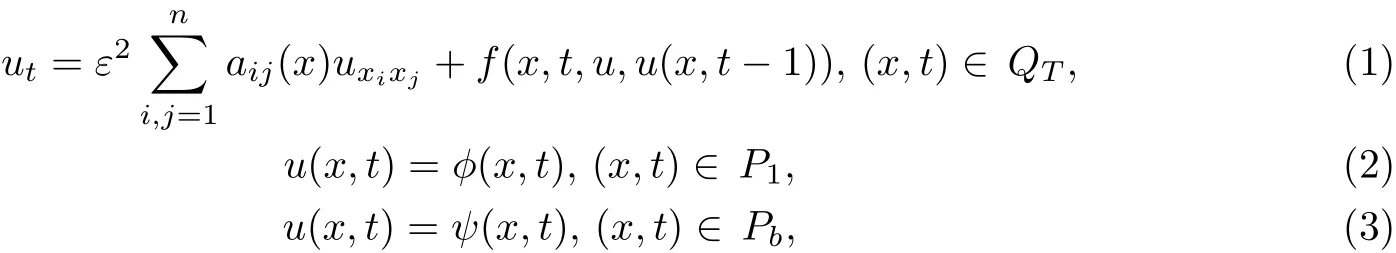
這里?∈Rn是有界凸區(qū)域,QT=?×[0,T],1＜T≤2,P1=??×[0,T],而Pb=?×[?1,0].

上述問(wèn)題包含了如Hutchinson[3]方程等來(lái)源于不同研究鄰域的多種問(wèn)題,有重要的研究?jī)r(jià)值.

現(xiàn)在作如下假設(shè):

[H1] 任取ξ∈

[H2]P1∈C2,

[H3] ψ(x,0)=?(x,0),x∈ ??.

用分步法對(duì)(1)-(3)進(jìn)行分析.在[0,1]上(1)-(3)可改寫(xiě)為:

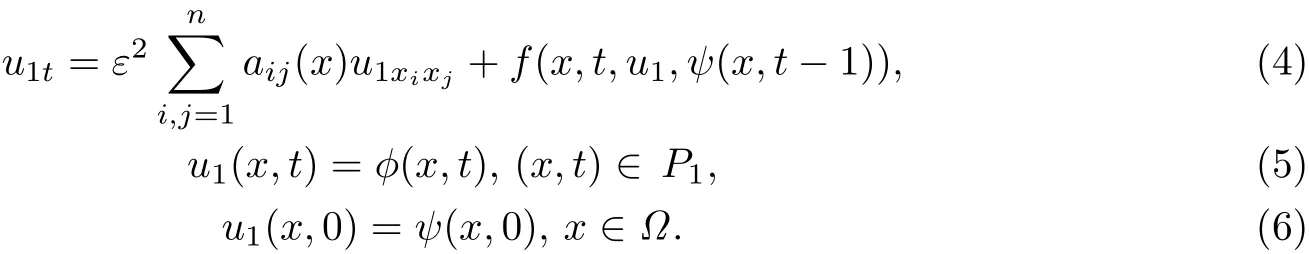
設(shè)(4)-(6)的解為u1(x,t),則在[1,T]上(1)-(3)為:

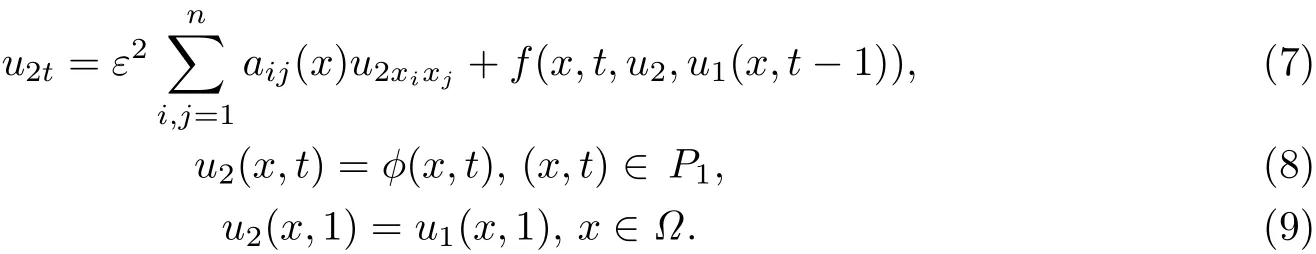
§2 形式漸近展開(kāi)式的構(gòu)造

首先從(4)-(9)開(kāi)始,構(gòu)造(1)-(3)的形式漸近展開(kāi)式.

設(shè)(4)-(6)的解為u1(x,t),而(7)-(9)的解為u2(x,t),則(1)-(3)的解為

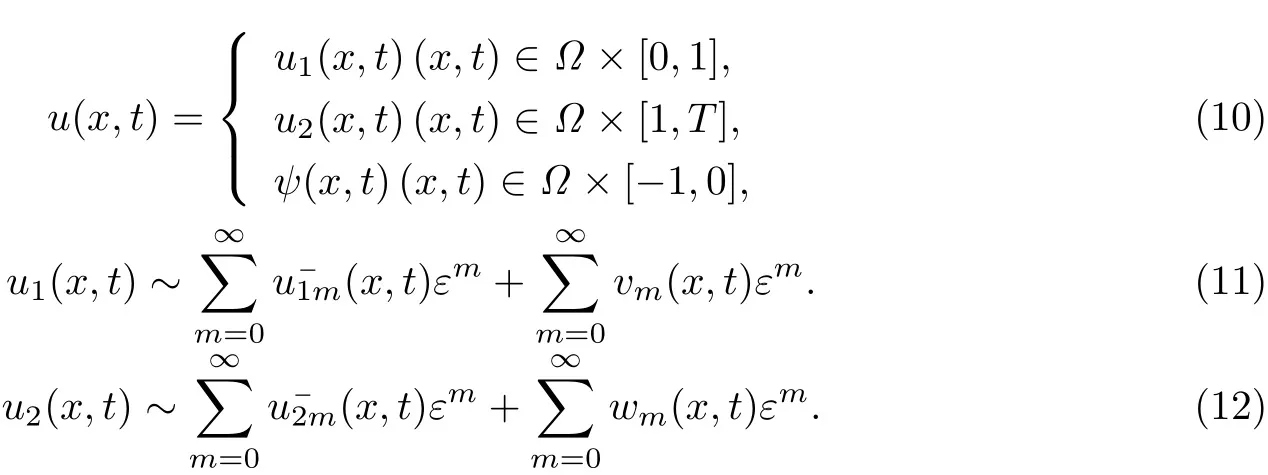
將(11)代入(4)-(6),并比較同次冪系數(shù)可得:

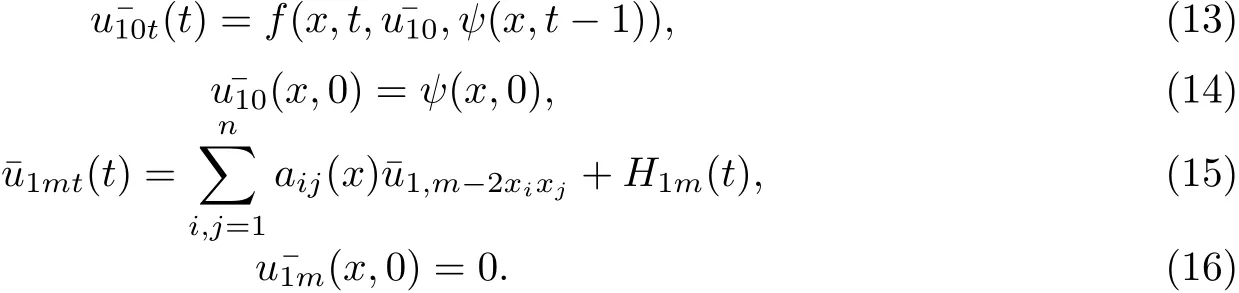
其中H1m是由和ψ(x,t?1)決定的函數(shù).

由于f(x,t,y,z)∈C1,α,所以(13)-(14)的解存在唯一,(15)-(16)是線性方程,其解存在唯一.將(12)代入(7)-(9),并比較同次冪系數(shù)可得:

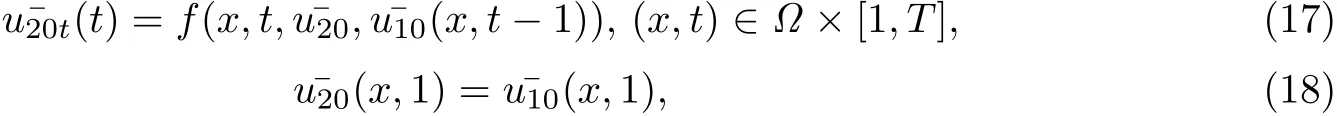
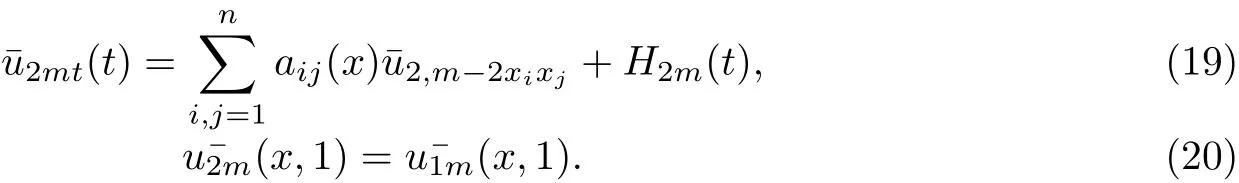
同理(17)-(20)的解存在唯一,所以構(gòu)造了(11)-(12)的正則部分的解.

現(xiàn)在構(gòu)造邊界層解,首先在??附近作局部坐標(biāo)變換,設(shè)新坐標(biāo)為(ρ,θ),x∈?為?內(nèi)在??附近的一點(diǎn),ρ =dist(x,??). 則沿著法線方向從??上一點(diǎn)Q到x,θ=(θ1,θ2,···,θn?1)是Q在n?1維流形??上的非奇異坐標(biāo),則x的坐標(biāo)為(ρ,θ).

在??的某鄰域內(nèi)(4)-(9)可以寫(xiě)作:

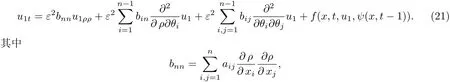
可得:

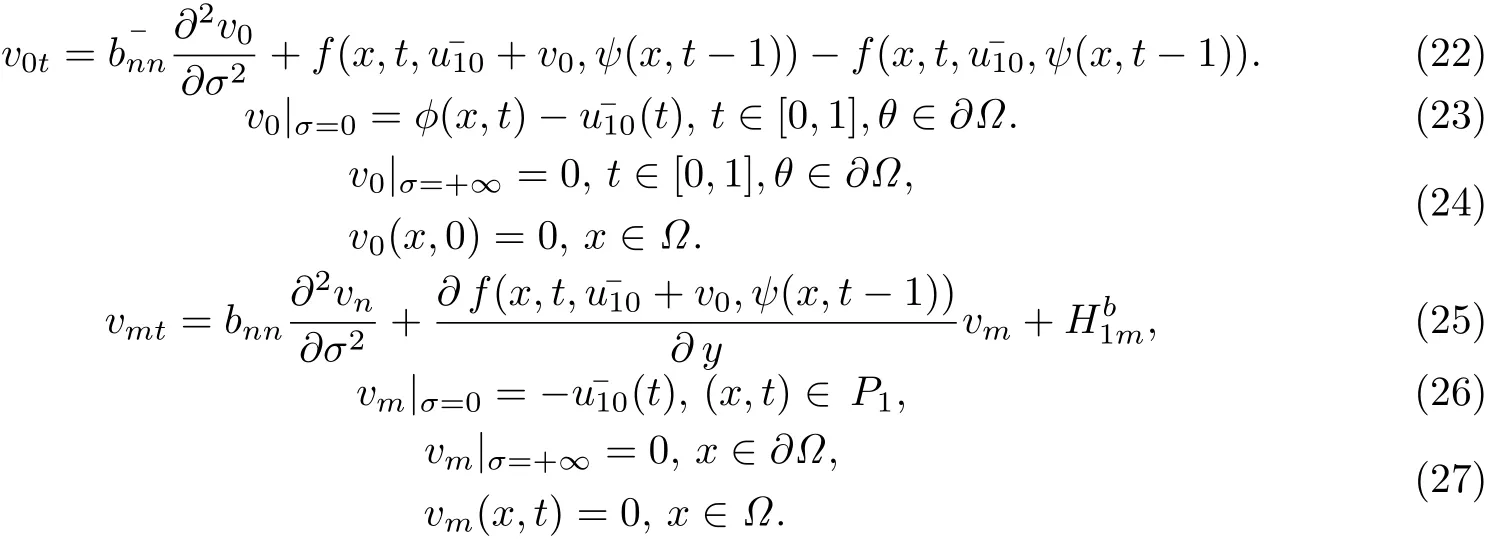
同理可得:

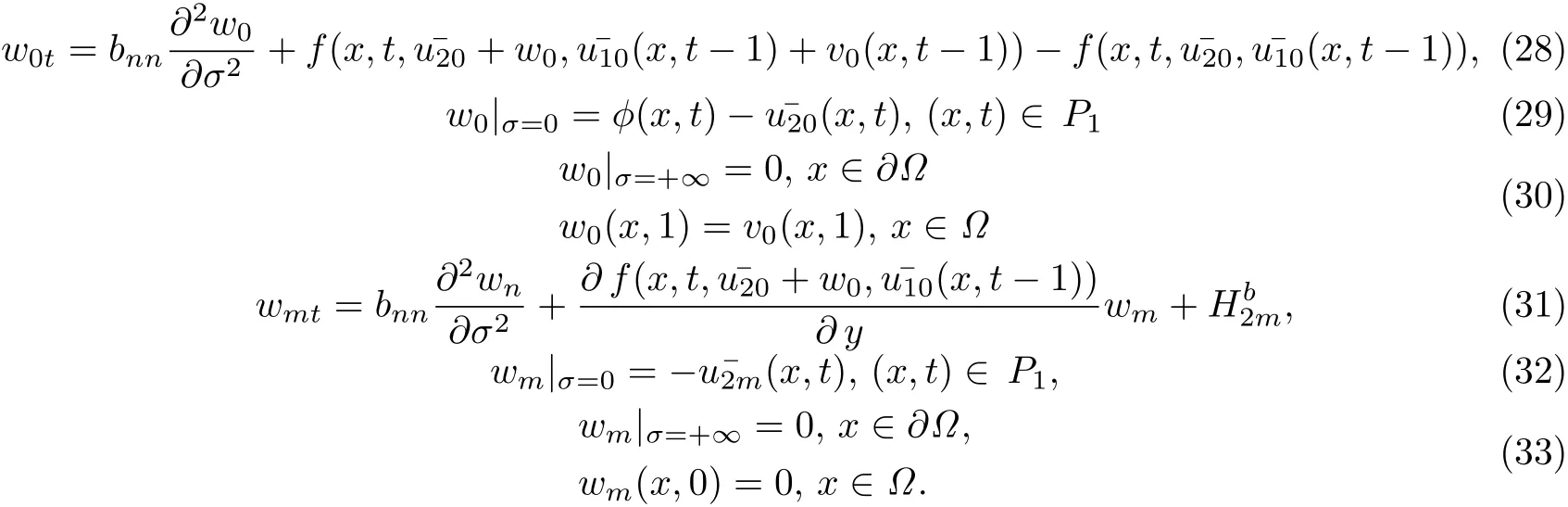
引理1(22)-(33)的解存在唯一.

證先證(22)-(24)的解唯一.設(shè)(22)-(24)有兩個(gè)解v1和v2,令w=v1?v2,則

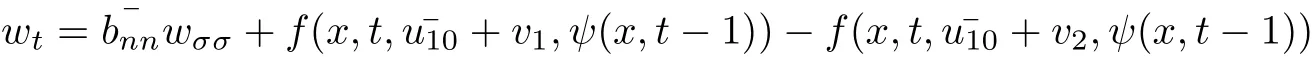
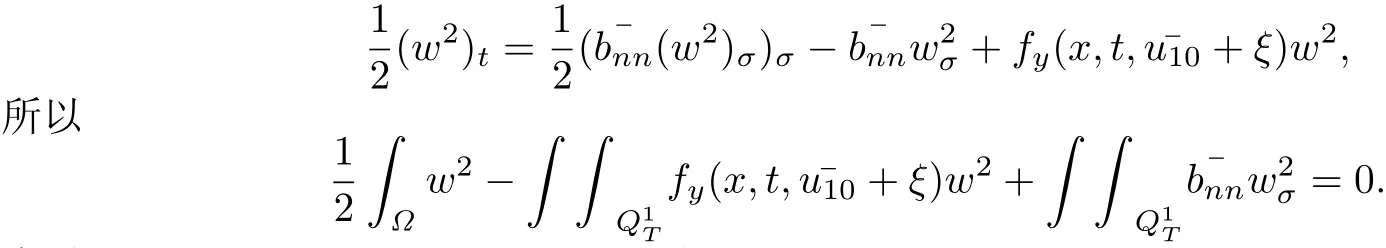
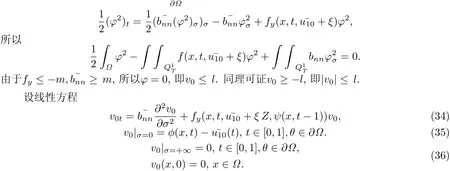
同理可證,(25)-(33)的解均存在唯一.

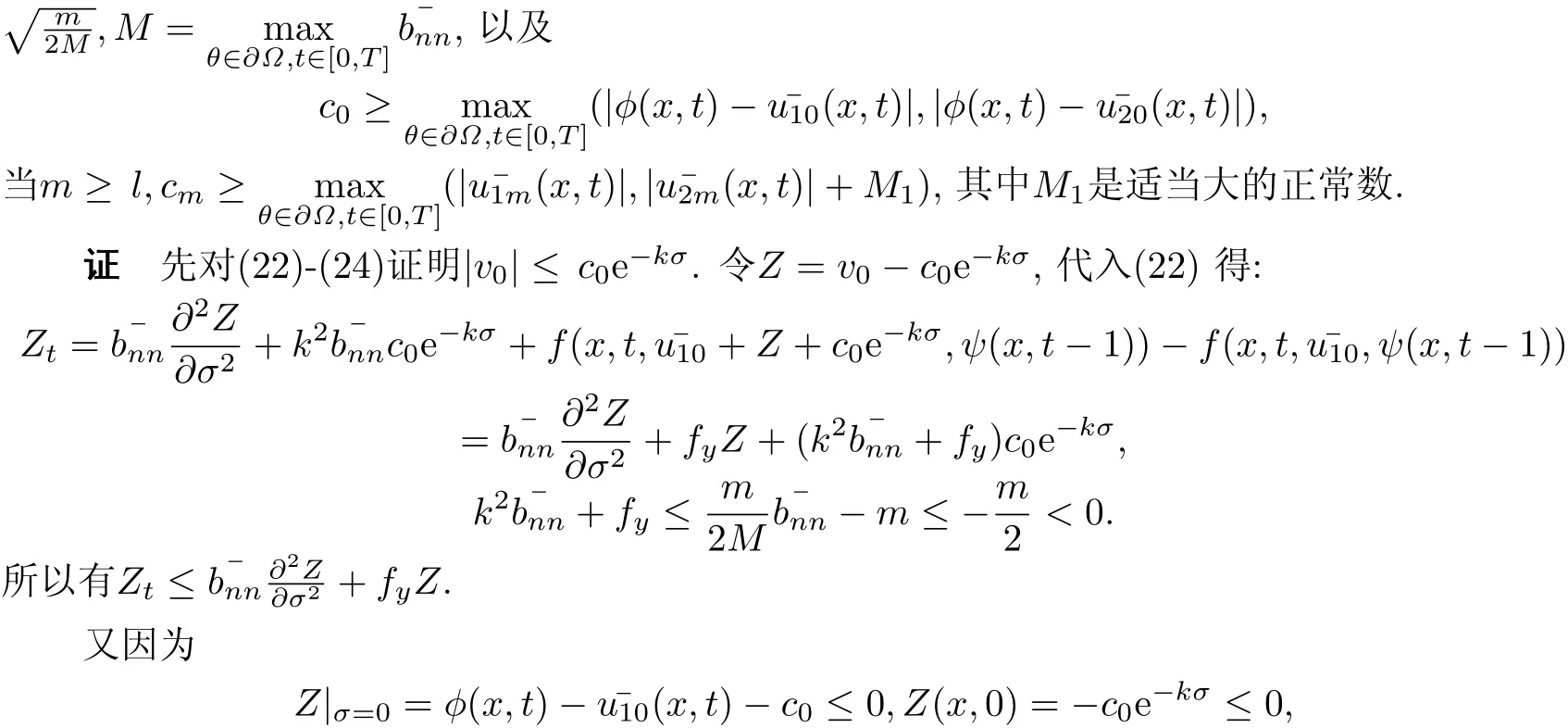
引理2(22)-(33)的解vn,wn,n=0,1,2,···,滿足這里k=所以由極大值原理可知,Z ≤ 0,即,同理可知,所以同理可證:顯然是正常數(shù). 令Z=則有

由于M1適當(dāng)大,因此所以由極大值原理知,同理可證,

至此,構(gòu)造了形式漸近解(11)和(12).

§3 解的存在唯一性

首先做(1)-(3)的解的最大值估計(jì)和Schuader估計(jì).

定理1(極值原理) 若(H1)-(H3)的條件滿足,令

同理對(duì)于w(x0,t0)=infQ1Tw(x,t)≤0,可以證得w(x0,t0)=0,即在同樣方式可證QT上w(x,t)≡0,即(1)-(3)的解唯一.

§4 余項(xiàng)估計(jì)

這里H2(x,t,ε)由已知的和wm決定,因此是有界的,即|H2(x,t,ε)|≤M,用上述同樣方式可證得即形式漸近展開(kāi)式(11)和(12)一致有效.

§5 結(jié)束語(yǔ)

文中對(duì)一類(lèi)半線性拋物型時(shí)滯偏微分方程的奇攝動(dòng)問(wèn)題進(jìn)行了分析.運(yùn)用邊界層校正方法構(gòu)造了形式漸近展開(kāi)式,證明了奇攝動(dòng)時(shí)滯半線性拋物型偏微分方程的極大值原理,從而得到了最大模估計(jì)和相應(yīng)的Schuader估計(jì),得到了在QT=?×[0,T]的柱狀區(qū)域上解的存在唯一性,其解是屬于的,得到了余項(xiàng)估計(jì),因此證明了漸近解的一致有效性.

[1] Ausari A R,Bakr S A,Shishkin G I.A parameter-robust fi nite di ff erence method for Singularly perturbed delay parabolic partial di ff erential equations[J].Journal of Computational and Applied Mathematics,2007,205:552-566.

[2] 莫嘉琪,姚靜蓀.一類(lèi)微分-差分反應(yīng)擴(kuò)散方程的漸近解[J].數(shù)學(xué)雜志,2011,311(1):133-137.

[3] Gourley S A.Travelling fronts in the di ff usive Nicholson’s blow fl ies equations with distributed delays[J].Mathematical and Computer Modelling,2000,32:843-853.

[4] Thandapani E,Savithri R.On Oscillation of a neutral partial functional di ff erential equations[J].Bulletin of the Institute of Mathematics Academia Sinica,2003,31(4):273-292.

[5] Pao Liu Chow.In fi nite-dimensional parabolic equations in Gauss-Sobolev spaces[J].Communications on Stochastic Analysis,2007,1(1):71-86.

[6] Xing Fuzou.Delay induced traveling wave fronts in reaction di ff usion equations of Kpp-Fisher type[J].Journal of Computational and Applied Mathematics,2002,146:309-321.

The asymptotic solution of a class of singular perturbed semi-linear delayed parabolic partial di ff erential equation

BAO Li-ping
(School of Science,Hangzhou Dianzi University,Hangzhou 310018,China)

In this paper,a class of initial boundary problem of the singular perturbed semi-linear delayed parabolic partial di ff erential equation is discussed.The formal asymptotic expansion of the problem is obtained.The maximum principle of the singular perturbed delayed semi-linear parabolic partial di ff erential equations is proved.Then,the maximum-norm estimation and Schauder estimation for this problem are obtained.By the maximum-norm estimation and Schauder estimation for this problem,the existence and uniqueness of the solution of the problem on the columnar zone is proved,and the uniformly valid estimation of the asymptotic expansion is gained.

singular perturbation;semi-linear;delay parabolic di ff erential equation;asymptotic expansion;Schauder estimation;maximum-norm estimation;estimation of the remainder

35B25;35K57

O175.12

A

:1000-4424(2016)03-0307-09

2015-11-25

2016-01-25

國(guó)家自然科學(xué)基金(51175134)