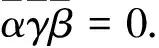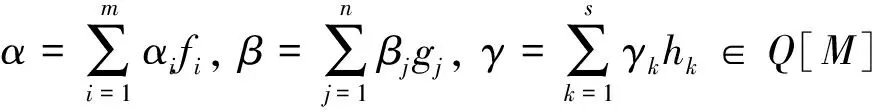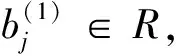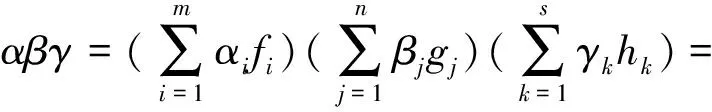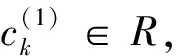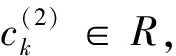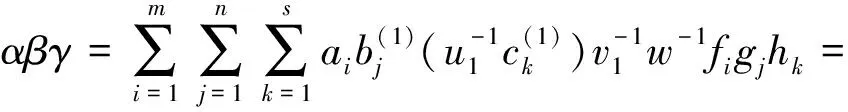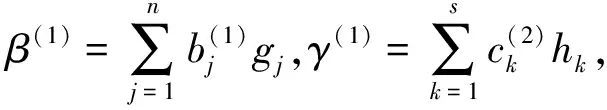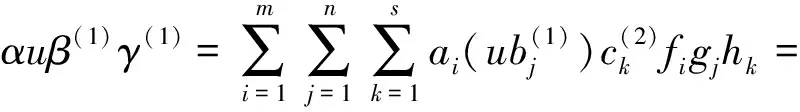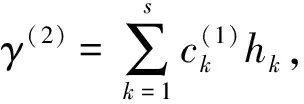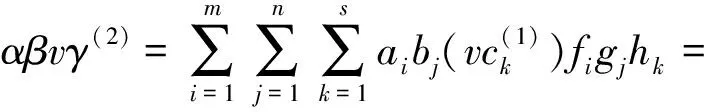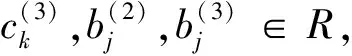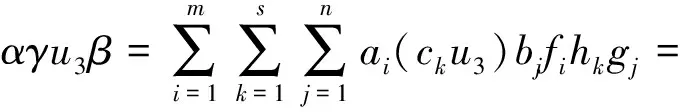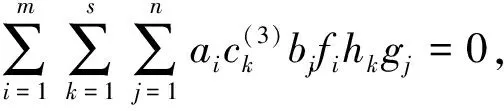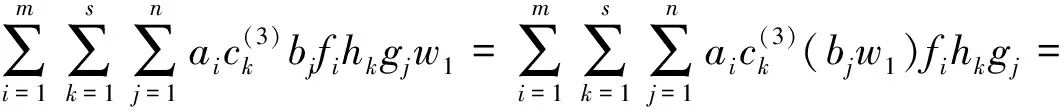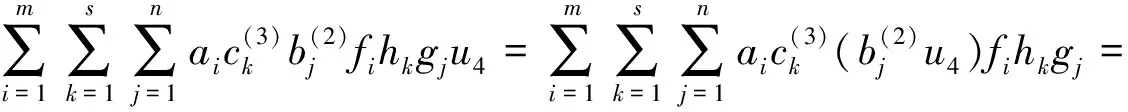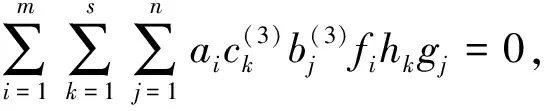M-強(qiáng)對(duì)稱(chēng)環(huán)
朱利民,吳 俊,費(fèi)盼盼
(安徽師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241000)
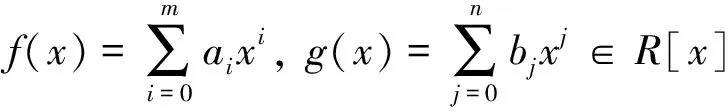
1 基本性質(zhì)
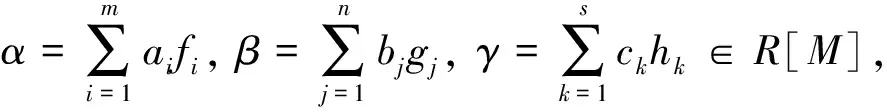
不難驗(yàn)證, 若M=(N,+), 則環(huán)R是M-強(qiáng)對(duì)稱(chēng)環(huán)當(dāng)且僅當(dāng)R是強(qiáng)對(duì)稱(chēng)環(huán).
稱(chēng)幺半群M為u.p.幺半群, 若對(duì)任意非空有限子集A,B?M, 存在g∈M, 使得g有唯一的表示g=ab,a∈A,b∈B.
引理1[6]若M是u.p.幺半群,R是約化環(huán), 則R[M]是約化環(huán).
命題1若M是u.p.幺半群,R是約化環(huán), 則R是M-強(qiáng)對(duì)稱(chēng)環(huán).
證明注意到若α,β∈R[M]使得αβ=0, 則(βα)2=β(αβ)α=0, 由引理1知R[M]是約化環(huán), 則βα=0.
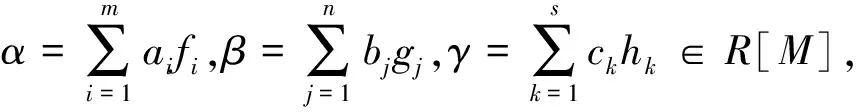
(M,≤)是有序幺半群, 若對(duì)任意的g1,g2,h∈M,g1 易知, 嚴(yán)格全序幺半群是u.p.幺半群. 推論1若M是嚴(yán)格全序幺半群,R是約化環(huán), 則R是M-強(qiáng)對(duì)稱(chēng)環(huán). 命題2設(shè)M是交換可消幺半群,N是M的理想, 若R是N-強(qiáng)對(duì)稱(chēng)環(huán), 則R是M- 強(qiáng)對(duì)稱(chēng)環(huán). 由于R是N-強(qiáng)對(duì)稱(chēng)環(huán), 故α1γ1β1=0, 所以αγβ=0, 即證R是M-強(qiáng)對(duì)稱(chēng)環(huán). 命題3設(shè)M是幺半群,N是M的子幺半群,若R是M-強(qiáng)對(duì)稱(chēng)環(huán), 則R是N-強(qiáng)對(duì)稱(chēng)環(huán). 引理2[5]設(shè)M,N是u.p.幺半群, 則M×N也是u.p.幺半群. 命題4設(shè)M,N是u.p.幺半群, 若R是約化的, 則R是M×N-強(qiáng)對(duì)稱(chēng)環(huán). 設(shè)T(G)是Abilian群G中所有有限階元素的集合, 則T(G)是G的完全正規(guī)子群. 稱(chēng)G是無(wú)撓的, 若T(G)={e}, 其中e是G的單位元. 命題5設(shè)G是有限生成的Abilian群, 若G是無(wú)撓的, 則存在環(huán)R使得R是G- 強(qiáng)對(duì)稱(chēng)環(huán). 證明設(shè)G是有限生成的Abilian群且T(G)={e}, 則G?Z×Z×…×Z, 群Z的有限直積. 由引理2知G是u.p.幺半群. 設(shè)R是約化環(huán), 則由命題1得到R是G-強(qiáng)對(duì)稱(chēng)環(huán). 命題6設(shè)R是環(huán),M是u.p.幺半群,I是R的理想, 若I是約化的, 且R/I是M-強(qiáng)對(duì)稱(chēng)環(huán), 則R是M-強(qiáng)對(duì)稱(chēng)環(huán). 推論2設(shè)M是嚴(yán)格全序幺半群, 若滿(mǎn)足下面條件之一, 則R是M-強(qiáng)對(duì)稱(chēng)環(huán). 1)R是約化環(huán). 2)R/I是M-強(qiáng)對(duì)稱(chēng)環(huán), 其中I是R的理想, 且I是約化的. 命題7若M,N是u.p.幺半群, 環(huán)R是約化的, 則R[M]是N-強(qiáng)對(duì)稱(chēng)環(huán). 證明若M是u.p.幺半群, 環(huán)R是約化的, 由引理1知,R[M]是約化的, 又N是u.p.幺半群, 由命題1即知R[M]是N-強(qiáng)對(duì)稱(chēng)環(huán). 設(shè)R為環(huán),M為R-R-雙模,R通過(guò)M的平凡擴(kuò)張T(R,M)=R⊕M, 其運(yùn)算是通常的加法和如下定義的乘法: (r1,m1)(r2,m2)=(r1r2,m1m2). 命題8設(shè)R是環(huán),M是u.p.幺半群, 若R是約化的, 則T(R,R)是M-強(qiáng)對(duì)稱(chēng)環(huán). 證明設(shè)α=(α0,α1),β=(β0,β1),γ=(γ0,γ1)∈T(R,R)[M] 滿(mǎn)足αβγ=0, 從而有下面等式: α0β0γ0=0, (1) α0β0γ1+α0β1γ0+α1β0γ0=0. (2) 由引理1知R[M]是約化環(huán), 從而R[M]是半交換環(huán), 于是有對(duì)任意α,β∈R[M],αβ2=0(或者α2β=0)有αβ=0. 由式(1)得到α0R[M]β0R[M]γ0=0. α0β0γ1+α1β0γ0=0. (3) 式(3)右乘γ0, 同上可得α1β0γ0=0. 故有 α0β0γ0=α0β0γ1=α0β1γ0=α1β0γ0=0. 由于R是M-強(qiáng)對(duì)稱(chēng)環(huán), 則 α0γ0β0=α0γ1β0=α0γ0β1=α1γ0β0=0. 所以αγβ=0, 即證T(R,R)是M-強(qiáng)對(duì)稱(chēng)環(huán). 定理1設(shè)e是環(huán)R的中心冪等元, Δ是R的中心正則元構(gòu)成的乘法閉集, 則下面敘述等價(jià): 1)R是M-強(qiáng)對(duì)稱(chēng)環(huán). 2)eR和(1-e)R是M-強(qiáng)對(duì)稱(chēng)環(huán). 3)Δ-1R是M-強(qiáng)對(duì)稱(chēng)環(huán). 證明1)?2) 設(shè)eα,eβ,eγ∈eR[M]使得eαeβeγ=0, 由于e是中心冪等元, 則有eαβγ=0. 又由R是M-強(qiáng)對(duì)稱(chēng)環(huán), 則eαγβ=0, 即eαeγeβ=0, 故eR是M-強(qiáng)對(duì)稱(chēng)環(huán). 同理可證(1-e)R是M-強(qiáng)對(duì)稱(chēng)環(huán). 2)?1) 設(shè)α,β,γ∈R[M]使得αβγ=0, 從而有eαeβeγ=0,(1-e)α(1-e)β(1-e)γ=0, 由于eR和(1-e)R是M-強(qiáng)對(duì)稱(chēng)環(huán), 則有eαeγeβ=0,(1-e)α(1-e)γ(1-e)β=0, 即eαγβ=0, (1-e)αγβ=0, 故αγβ=0. 3)?1)R是Δ-1R的子環(huán). 設(shè)M是幺半群,N是M的子幺半群, 稱(chēng)N是M的理想, 若對(duì)任意的n∈N,m∈M, 有nm∈N,mn∈N. 環(huán)R稱(chēng)為右Ore環(huán)[7], 若a,b∈R,b是正則元, 則存在a1,b1∈R,b1是正則元, 使得ab1=ba1. 由Ore定理可知,R是右Ore環(huán)當(dāng)且僅當(dāng)存在R的古典右商環(huán)Q. 定理2設(shè)M是幺半群, 若存在環(huán)R的古典右商環(huán)Q, 則R是M-強(qiáng)對(duì)稱(chēng)環(huán)當(dāng)且僅當(dāng)Q是M-強(qiáng)對(duì)稱(chēng)環(huán). 則αβγ=0, 由于R是M-強(qiáng)對(duì)稱(chēng)環(huán), 則αγβ=0. 由于αγβ=0, 則 [1] Lambek J. On the representation of modules by sheaves of factor modules[J]. Canad Math Bull,1971,14(3):359-368. [2] Ren Y L, Xu Z X. Strongly symmetric rings[J]. Math Pract Theory,2010,40(19):225-230. [3] Kim N K, Nam S B, Kim J Y. On simple singular GP-injective modules[J].Comm Algebra,1999,27(5):2087-2096. [4] Rege M B, Chhawchharia S. Armendariz rings[J]. Proc Japan Acad Ser A:Math Sci,1997,73(1):14-17. [5] Liu Z K. Armendariz rings relative to a monoid[J]. Comm Algebra,2005,33(3):649-661. [6] Singh A B, Juyal P, Khan M R,etal. Strongly reversible rings relative to monoid[J]. Int J Pure Appl Math,2010,63(1):1-7. [7] McConnell J C, Robson J C. Noncommutative noetherian rings[M]. New York: Wiley,1987.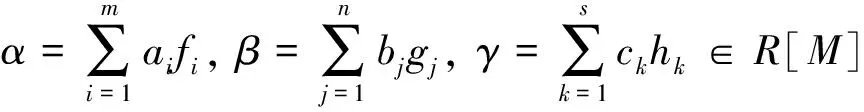
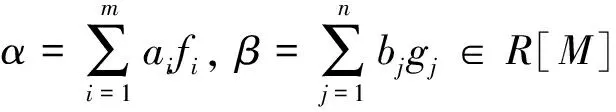
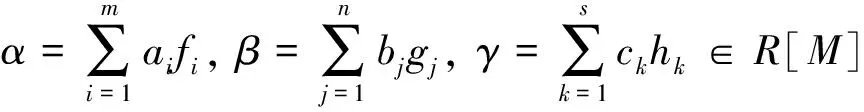
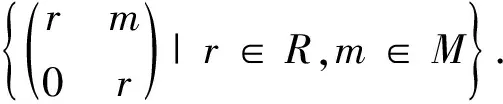
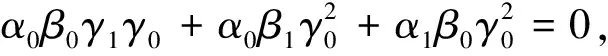
2 等價(jià)刻畫(huà)