A hybrid voxel sampling method for constructing Rad-HUMAN phantom?
ZHAO Kai(趙凱),CHENG Meng-Yun(程夢云),LONG Peng-Cheng(龍鵬程),FAN Yan-Chang(范言昌),WANG Wen(王文),HU Li-Qin(胡麗琴),and WU Yi-Can(吳宜燦),
1Institute of Nuclear Energy Safety Technology,Chinese Academy of Sciences,Hefei 230031,China
2Institute of Public Computer,Hefei Normal University,Hefei 230601,China
A hybrid voxel sampling method for constructing Rad-HUMAN phantom?
ZHAO Kai(趙凱),1,2CHENG Meng-Yun(程夢云),1LONG Peng-Cheng(龍鵬程),1FAN Yan-Chang(范言昌),1WANG Wen(王文),1HU Li-Qin(胡麗琴),1and WU Yi-Can(吳宜燦)1,?
1Institute of Nuclear Energy Safety Technology,Chinese Academy of Sciences,Hefei 230031,China
2Institute of Public Computer,Hefei Normal University,Hefei 230601,China
An accurate and fast sampling method was developed on the modeling of a voxel phantom called Rad-HUMAN for radiation protection of MC-based radiation transport and simulation.The segmented organ voxels, which were assigned with three dimensional(3D)coordinates,were simplif i ed through a two-step hybrid sampling algorithm.Firstly,certain voxels were sampled into a coordinate matrix by the nearest neighbor sampling. Secondly,the coordinate matrix was renewed using a weighted sampling.To compare visualization with the sampling,the resultant matrix was used to extract the contour of organs/tissues for constructing polygon-surface phantom.The feasibility and effectiveness of the sampling method was verif i ed through the modeling of large organs(e.g.skeleton system)and application of transformation to MC computational geometries.
Sampling,Monte Carlo,Voxel,3D,Rad-HUMAN
I.INTRODUCTION
Computational phantoms have been used extensively in radiation protection for Monte Carlo(MC)-based radiation transport and simulation[1].Accuracy of the phantom plays a critical role in dose calculation[2,3],and computational phantoms based on color photographic images and containing detailed information of human body have been developed in many countries[4,6].However,it is a big problem to deal with the massive voxels accurately[5].Lots of ref i nement methods were developed not directly focusing on the original voxels,and sometimes voxels were sampled with interpolation.This may generate some ambiguity that may cause serious problem in whole-body phantom construction.Due to limitation of computer performance,the large organs(e.g. skeleton system)from the image slices cannot be constructed as a whole accurately.
Based on high-resolution sectioned images of a Chinese Visible Human(CVH)dataset,a voxel phantom called Rad-HUMAN(Accurate whole-body computational phantom of Chinese adult female)was established by the FDS Team(www.fds.org.cn).
This CVH data set,which contains 3641 slices with 3286×1586 pixel resolution,was obtained from a Chinese female cadaver.Each voxel size of the data set is 0.15mm×0.15mm×0.25mm for the head and neck and 0.15mm×0.15mm×0.5mm for the rest of the body.The total number of the voxels is about 16.8 billion.Segmentation[6](Fig.1)was processed manually and calibratedby MCAM(Multi-Physics Coupling Analysis Modeling Program)developed by the FDS Team[7–9].In addition to the fact that the voxel phantom was diff i cult for Monte Carlo dose calculation,demonstrating its geometry was also laborious[6].

Fig.1.(Color online)Organ segmentation.
In this work,a f l exible sampling method was investigated on the modeling of Rad-HUMAN voxel phantom.Based on the method,the visualization was compared and computational geometries for Monte Carlo dose calculation was discussed.
II.VOXEL SAMPLING METHOD
A.Nearest neighbor sampling
After segmentation,the organs had different RGB colors to be distinguished.In this paper,the data set of voxels assigned with 3D coordinates can be written as
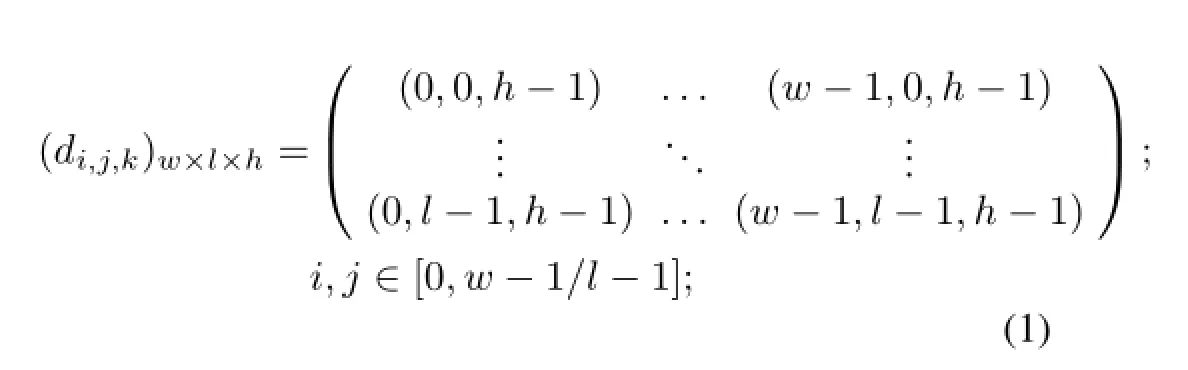
wherew,landhare the width,length and height of the CVH dataset,respectively;andi,jandkare the position subscripts of the voxels.
It is no use obtaining all the voxels of a certain organ to arduously construct its model.In the nearest neighbor sampling,the segmented voxels are appropriately enlarged and sampled from their nearest neighbors.
Change the voxel array fromw×l×ntow′×l′×n′,the sampling enlargement factor can be expressed as
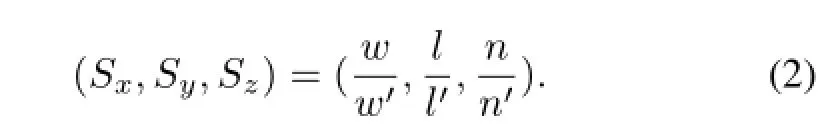
To be in consistence with the later sampling,the voxel coordinate of an organ can be described as a sparse matrixα
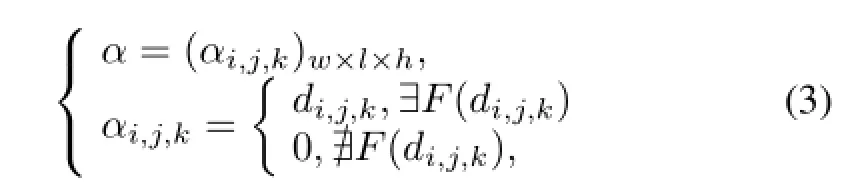
where?F(di,j,k)(or?F(di,j,k))means thatdi,j,kis(or not)a coordinate of the original organ.
In the nearest neighbor sampling,the sampled organf(x,y,z)is acquired from an original organF(X,Y,Z)described as
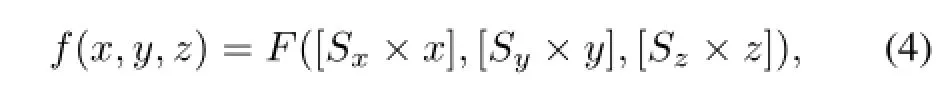
where symbol“[]”stands for rounding off the number for the result.So the resultant coordinate matrix of the sampled organ can be described as
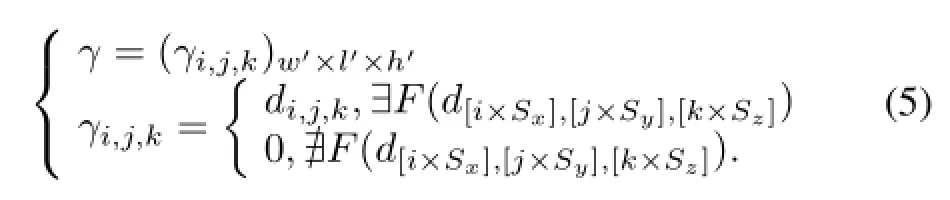
To decrease the demand for computer memory,in present study,the nonzero coordinate(γi,j,k)was stored on disk as fi le format corresponded with exclusive address for compressed storage.
B.Weighted sampling
As accuracy loss is serious by the nearest sampling,a weighted sampling in the present study was proposed.With the same enlargement factor def i ned in Eq.(2),a sampling unit can be enclosed by a lattice with a size ofSx×Sy×Sz. Obviously the voxels in the lattice cannot always belong to one organ,hence a weighted factor to judge whether the voxels of the sampling unit can be regard as a voxel after sampling.
After sampling,the relative position of the voxel was changed corresponding with the sampled voxel array(w′× l′×n′).That is,the coordinates must be zoomed by a size of(1/Sx)×(1/Sy)×(1/Sz)for the consistence.In addition,described as the coordinates with exclusive addresses, the original voxels of the lattice can be projected to a new address of the sampled storage.This brought the effectiveness for numbering the amounts of the voxels which belong to one organ being projected.So according to a def i ned weight of the voxels in the lattice,the voxels of a certain organ can be sampled fast.The detailed steps for the weighted sampling are as follows.
Step 1:Obtain coordinate matrixαof an organ referred as Eq.(3).
Step 2:Map the matrixαto a sampling matrixβ.Supposing (xα,yα,zα)is an element ofα,the element ofβbecomes
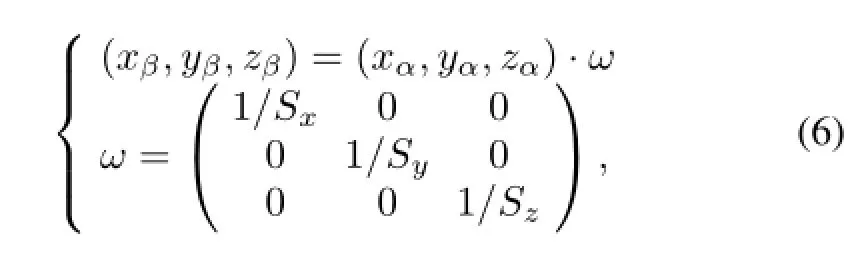
where the mapped address inβcan be described asθwith the element obtained from

ωandτin Eq.(7)are factors to multiply every element ofα.
Step 3:Record the weights of certain coordinates which are mapped into the same locations. Let(x,y,z)be a coordinate after sampling,which are mapped fromσ(a region of sampling lattice).
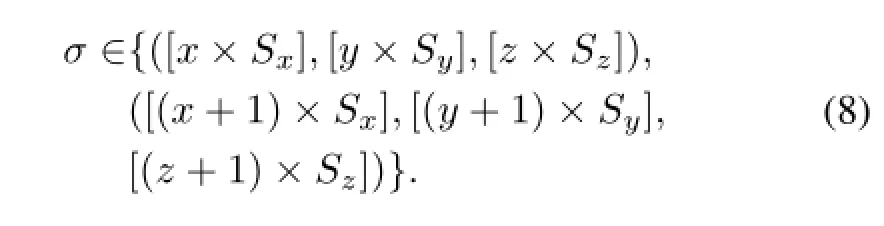
In this step,the coordinates inσis stored at the same location withδ(x,y,z)recording their amounts.
Step 4:Filter the coordinates fromβ,with the weights of no less than a weight factor. Supposing that the weights were de fi ned as the proportional amounts of the sampling unit which is 0.5,the fi lteredcoordinatematrixγcanbeselectedfromβwith the condition of
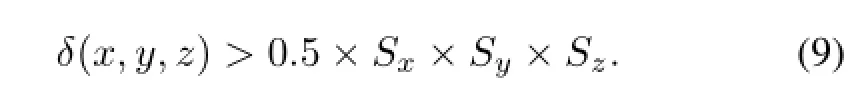
The resultant coordinate matrixγcan also be stored on disk as f i le format in sequential order.
C.Hybrid voxel sampling
The nearest sampling is a fast way to reduce the data size. However,it is not recommended to use this sampling method on some smaller data because of serious accuracy losses.In this paper,we combine it with the weighted sampling as a two-step hybrid sampling algorithm.In the hybrid sampling, the sampling unit is divided into smaller lattices for the nearest sampling,and then the smaller lattice can be assighed with weights for the weighted sampling.
To that end,the enlargement factor of(Sx,Sy,Sz)was divided into(Nx,Ny,Nz)and(Px,Py,Pz)for the nearest sampling and the proportional sampling,respectively.
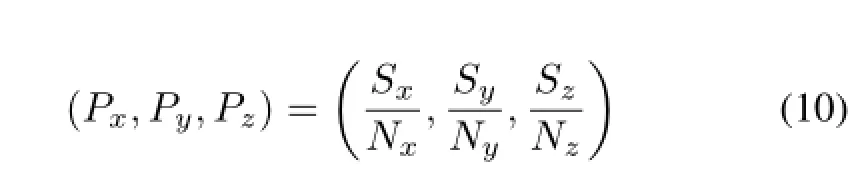
Using an enlargement factor of(Nx,Ny,Nz)for the nearest sampling,the original coordinate matrix can be obtained according to Eq.(5)where
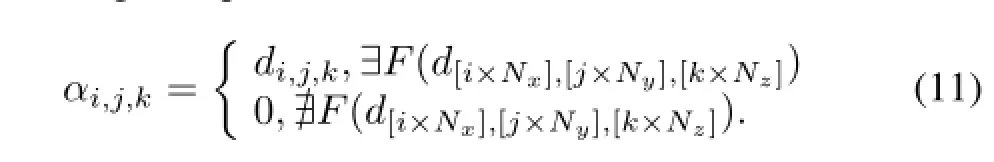
In order to combine the nearest sampling with the weighted sampling for the hybrid sampling,the factor in Eqs.(6) and(7)for the mapping and locating becomes
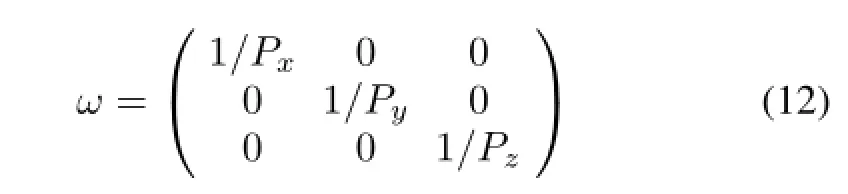
andτ=(1/Px,w/(Py×Sx),w×l/(Pz×Sx×Sy)),respectively.
The detailed steps to implement the hybrid sampling algorithm are shown in Fig.2.
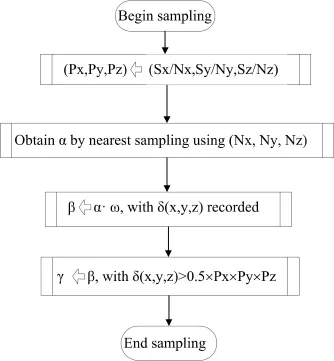
Fig.2.Hybrid voxel sampling algorithm.
III.RESULTS AND DISCUSSION
A.Application in construction of polygon-surface phantom
The organs or tissues of interest(e.g.,lungs,liver,skin etc.)from the original tomographic photography were identifi ed by assigning every pixel with an identi fi cation numbers. All these numbers can be stored sequentially as a pixel matrix that can be used to extract equivalent matrix,from whichthe polygon-surface model can be constructed by Marching Cubes[10].
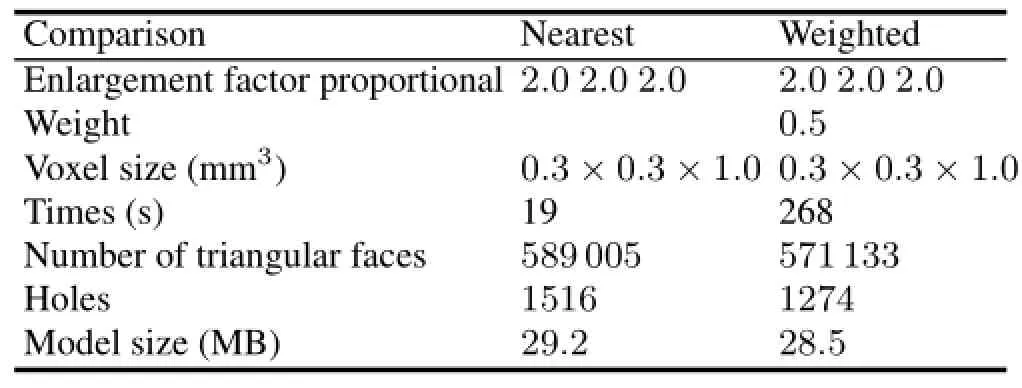
TABLE 1.The comparison of the heart reconstruction
The equivalent matrix can be acquired by the last step of the sampling method.For example in weighted sampling,on purpose of generating the matrixγ,the coordinates satisfying the condition ofδ(x,y,z)>0.5×Sx×Sy×Szare set as an identif i cation number,while the coordinates not satisfying that condition are set as another identif i cation number.The changed matrixγcan then be used as the equivalent matrix using VTK toolkit to generate the polygon-surface model.
Preparatorily,these sampling methods were processed with the just one CPU of the 3.10GHz Intel CoreTM2Quad Processor i5-2400 64bit operating system.To compare with two special cases of the hybrid sampling,the construction of heart organ containing 265 slices was taken for example.Def i ning the proportional amounts as the weights,Table 1 presents relevant sampling parameters between the nearest and the weighted sampling methods which are compared by the visualization in Figs.3(a)and 3(b).
When the voxel increased with a factor of 2.0 inx,yandzdirections,the time expenditure by the nearest sampling was about 7.09%of that by the proportional sampling.The number of the holes and model size produced by the weighted sampling was 84%and 95%of the one produced by the nearest sampling,respectively.By the weighted sampling,the incorrect model incurred by segmentation can be repaired (Fig.3(d)).
Parameters between the two methods(Table 1)are mainly dependent on computer performance and data set resolution etc.For precision adjustment,the proportional weight factor can be used.
B.Improvement on the sampling and analysis
The nearest and the weighted sampling method in present paper are implied as two special cases of the hybrid sampling.To discuss their combined criteria,extra experiment was taken with a large organ(e.g.skeleton system,include marrow,pelvis,cartilage etc.).With the same enlargement size of 4.0×4.0×4.0 and a proportional weight of 0.5 for the proportional and the hybrid method,modeling parameters between the three samplings are given in Table 2 and the visualization comparison is illustrated in Fig.4.
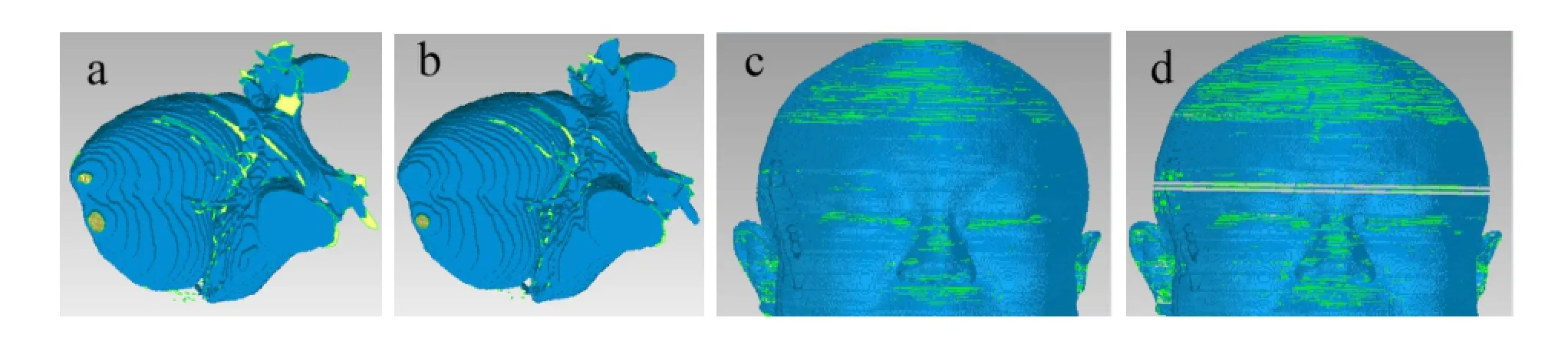
Fig.3.(Color online)Heart and face model sampling comparisons.(a)Heart model by the nearest sampling.(b)Heart model by the proportional sampling.(c)Face model by the nearest sampling.(d)Face model by the proportional sampling

TABLE 2.The comparison of the skeleton system reconstruction
In the hybrid sampling,the enlargement size of 4.0×4.0×4.0 was divided to 2.0×2.0×2.0 for both the nearest and weighted.The time expenditure by the hybrid sampling was about 18.15%of that by proportional.In addition,the hole number of the model produced by the hybrid was about 16.43 percent of that produced by the nearest.It is advantageous to create the model accurately and quickly for visualization[11, 12].The visualization of the model constructed by the three sampling is shown in Fig.4.
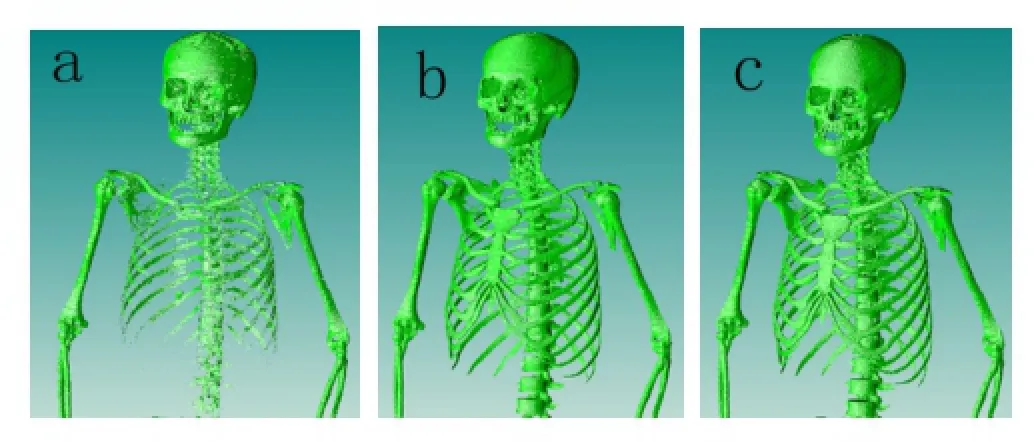
Fig.4.(Color online)Visualization comparisons between three sampling methods.(a)Skeleton system of upper half of the body by the nearest sampling.(b)Skeleton system of upper half of the body by the proportional sampling.(c)Skeleton system of upper half of the body by the hybrid sampling.
Thenearestsamplingmaycauseseveredistortion (Fig.4(a))when the sampling enlargement factor becomes larger.The hybrid sampling,therefore,is an appropriate method to make up for such def i ciency and enhance the process.It is a f l exible sampling method to be evolved from the one to another with a distributed enlargement factor.The combined criterion depends on the sampling ratio,dataset size,computer performance etc.Generally,considering the visual impact,the enlargement size allocated for the nearest sampling shall not be larger than 2.0×2.0×2.0.This can largely reduce the data size for fast processing with current conf i guration of a personal computer.For the demanding of more accuracy of the model(Figs.4(b)and 4(c)),the enlargement factor allocated for the weighted sampling should be larger.Because there are many organs contained in the whole phantom,the accepted time to visualize and check the geometry of the phantom can be satisf i ed by the hybrid sampling.
From Table 2,the percent of holes to faces of the nearest,the weighted and the hybrid is 1.26%,0.17%and 0.20%, respectively.Compared with the visualization of Fig.4,the percent of about 0.20%with the model can be as a reference acceptance criteria for better visualization.
By the hybrid sampling,the voxels are enlarged by a factor of 4.0×4.0×4.0,the whole skeleton system can be shown in Fig.5.
C.Application in Monte Carlo computational geometries
For dose calculation in lattice geometry,the methods presented in this paper can be applied[13].In this case for Monte Carlo simulation,the pixel matrix of the whole phantom should be generated.
The weights def i nition can be designed by the material, density or other biological property.Next,accumulate the weights from the resultant coordinate matrix(e.g.γ),locate the voxel in the pixel matrix satisfying the weighted factor, and assign it with the identif i cation number.Finally,the pixel matrixes of body can be transferred to lattice representation geometry in MCNP codes[14,15].
However,in addition to the lattice geometry[16,17],the polygon-surface model,which is constructed by Marching Cubes[18],can hardly avoid surface intersections and holes in quality.For dose calculations with deformable phantoms[19,20],repairing/improvement(e.g.f i lling,relaxation)is needed,so as to conf i rm no imperfection or interfer-ence,and to transfer it into those accepted by MC codes(e.g. MCNP,Geant4,etc.).
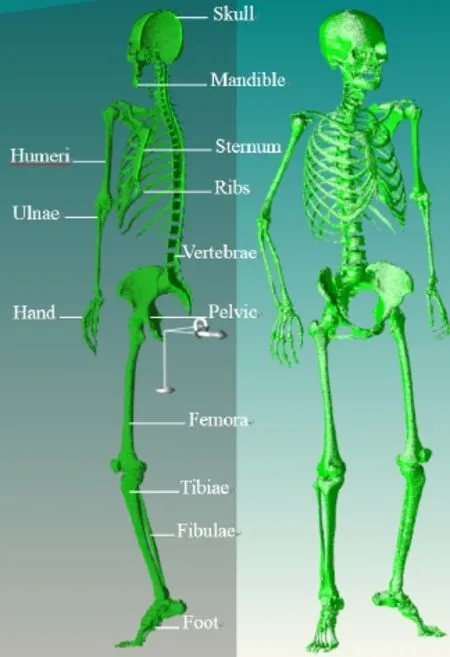
Fig.5.(Color online)High-accuracy skeleton system by the hybrid sampling.
IV.CONCLUSION
In this paper,a hybrid voxel sampling algorithm,which merged the nearest sampling and a weighted sampling,was put forward.Through discussions of the model construction, the three sampling methods are able to deal with mass voxels. For accurate sampling,the weighted and the hybrid sampling are effective.As a f l exible sampling,the hybrid sampling is able to show high-performance especially on construction of large organs.It is a valid sampling method on the visualization of the(MC)geometries of human voxel phantom.
Furthermore,based on these methods,the geometries for Monte Carlo dose calculation were then analyzed.The phantom of polygon-surface geometry or lattice representation geometry is able to be transferred to MC codes for dose calculations.Finally,by the proposed sampling,more accurate CAD(Computer Aided Design)(STEP etc.)model can be constructed in the f i eld of medical diagnosis and other scientif i c researches.
ACKNOWLEDGEMENTS
The authors wish to thank Prof.Zhang Shao-Xiang and his group in No.3 Military Medical University of China for providing the visible human anatomical data set and the FDS Team for their support.
[1]Wu Y C,Song G,Cao R F,et al.Chinese Phys C,2008,32: 77–182.
[2]Zhao F,Xue Y,Chen Y,et al.Nucl Sci Tech,2011,22:144–150.
[3]Yang J B,Tuo X G,Li Z,et al.Nucl Sci Tech,2010,21:221–226.
[4]LiuY,XieTW,LiuQ,etal.NuclSciTech,2011,22:144–150.
[5]Zhang Q H,Hui W H,Wang D,et al.Nucl Sci Tech,2010,21: 177–181.
[6]Xu X G,Echerman K F.Handbook of Anatomical Models for Radiation Dosimetry,New York,CRC Press,2009:136–285.
[7]Li Y,Lu L,Ding A P,et al.Fusion Eng Des,2007,82:2861–2866.
[8]Lu L,Lee Y K,J J Zhang,et al.Nucl Instrum Meth A,2009,605:384–387.
[9]Zeng Q,Lu L,Ding A,et al.Fusion Eng Des,2006,81:2773–2778.
[10]Li J,Huang S Q,Li G,et al.2010 3rdInternational Congress on Image and Signal Processing,ISP2010,2396–2400.
[11]Ando M.Maksimenko A,Yuasa T,et al.Nucl Sci Tech,2006,17:389–395.
[12]Askri B,Trabelsi A,Baccari B,et al.Nucl Sci Tech,2008,19: 358–364.
[13]Gou C J,Li X,Hou Q,et al.Nucl Sci Tech,2011,22:349–352.
[14]Wu Y C,FDS Team,Fusion Eng Des,2009,84:1987–1992.
[15]KimCH,JeongJH,BolchWE,etal.PhysMedBiol,2011,56: 3137–3161.
[16]Zeng Q,Lu L,Ding A,et al.Fusion Eng Des,2006,81:2773–2778.
[17]Zeng Q,Long P C,Zou J,et al.AIP Conf Proc,2012,1442: 265–266.
[18]LorensenWEandClineHE.CompGraph,ACMSiggraph’87, Conference Proceedings,1987,21:163–169.
[19]Xu X G,Chao T C,Bozkurt A.Health Phys,2000,78:476–486.
[20]Schimmerling W,Cucinotta F A,Wilson J W.Adv Space Res, 2003,31:27–34.
10.13538/j.1001-8042/nst.25.020503
(Received May 31,2013;accepted in revised form November 8,2013;published online March 20,2014)
?Supported by National Special Program for ITER(No.2011GB113006), Strategic Priority Research Program of Chinese Academy of Sciences (No.XDA03040000),National Natural Science Foundation of China(No. 91026004),the Knowledge Innovation Projects of Chinese Academy of Sciences(No.095CF2R211)and the Key Foundation for Young Talents in College of Anhui Province(No.2013SQRL063ZD)
?Corresponding author,yican.wu@fds.org.cn
 Nuclear Science and Techniques2014年2期
Nuclear Science and Techniques2014年2期
- Nuclear Science and Techniques的其它文章
- Measurement of keffwith an improved neutron source multiplication method based on numerical analysis?
- Simulation of neutron diffusion and transient analysis of MSR?
- Ordered water monolayer on ionic model substrates studied by molecular dynamics simulations?
- A method for determination of the s orbital component of12Be ground state?
- Demonstration of Pm-147 GaN betavoltaic cells
- Upgrade to the front-end electronics of the BESIII muon identif i cation system
