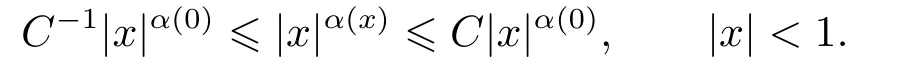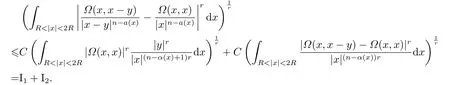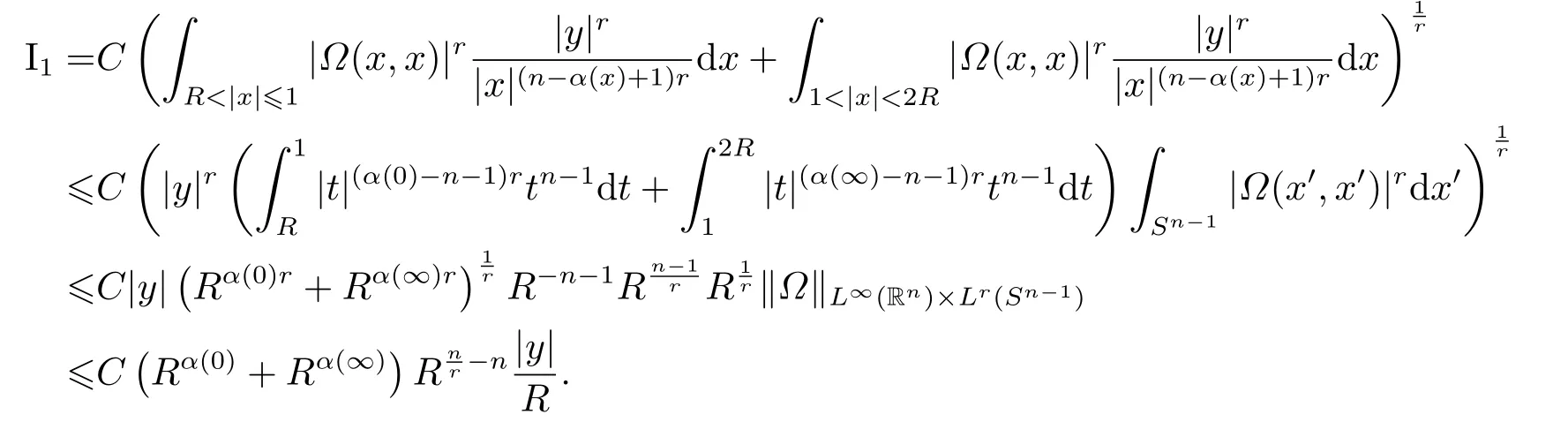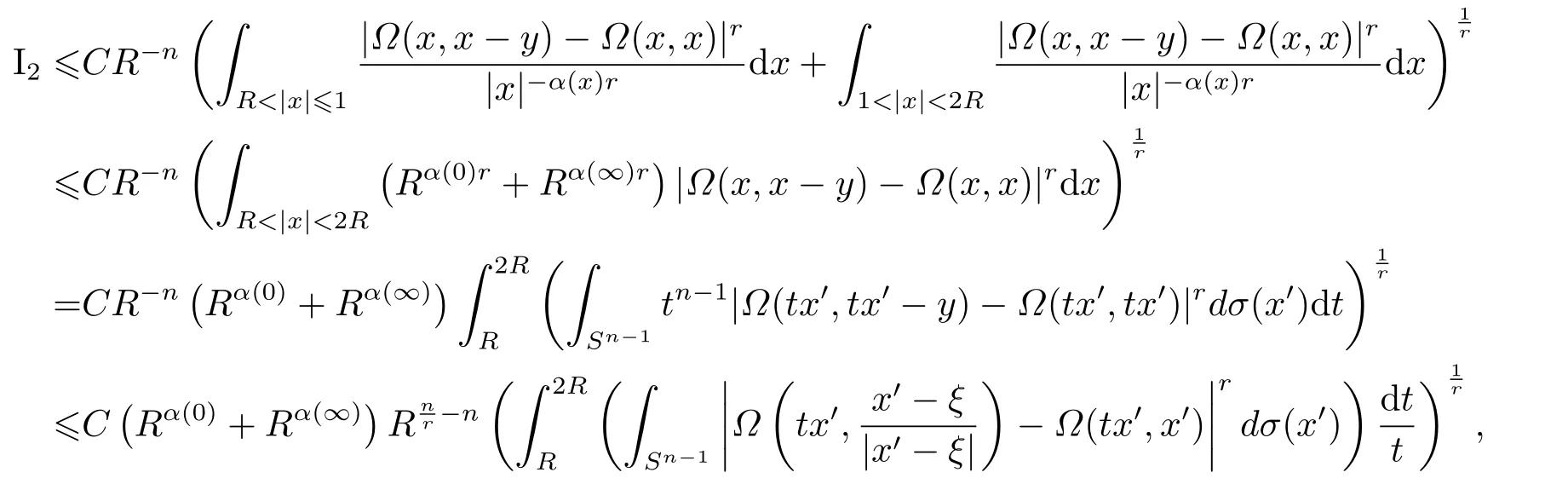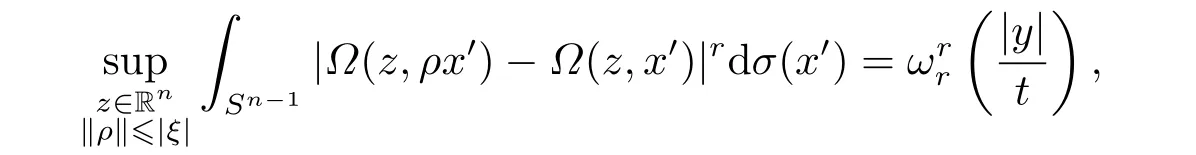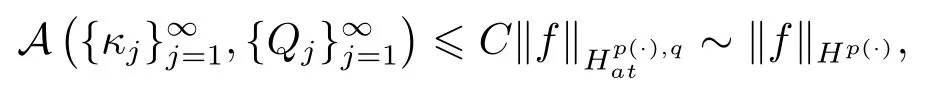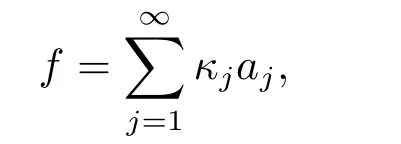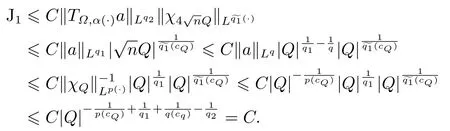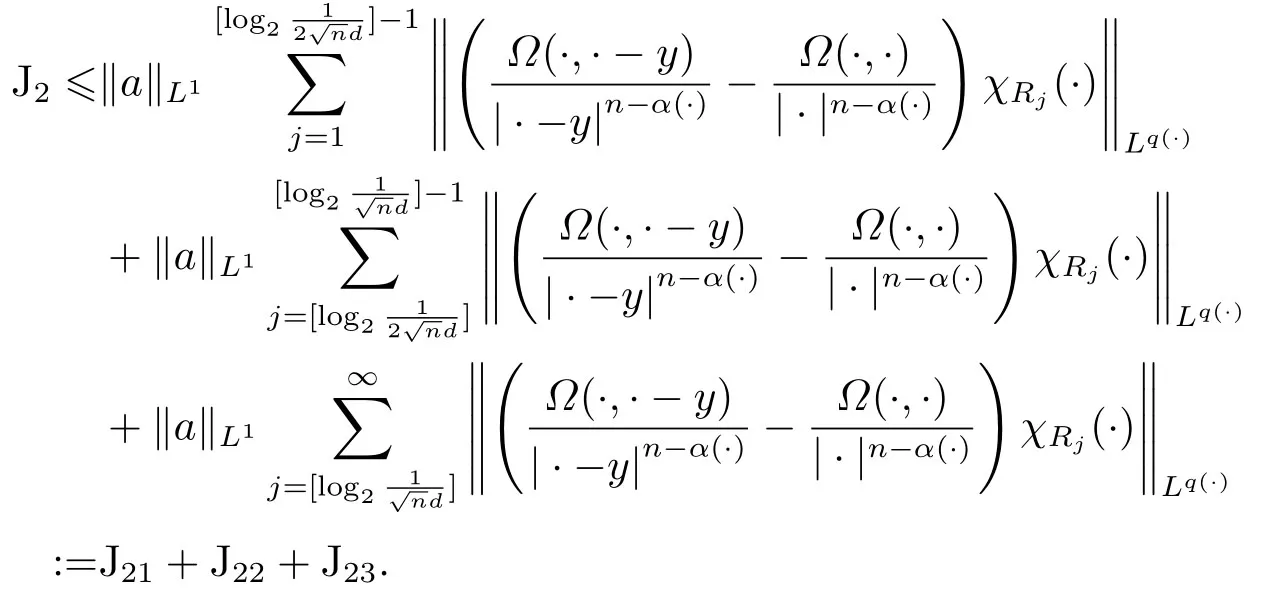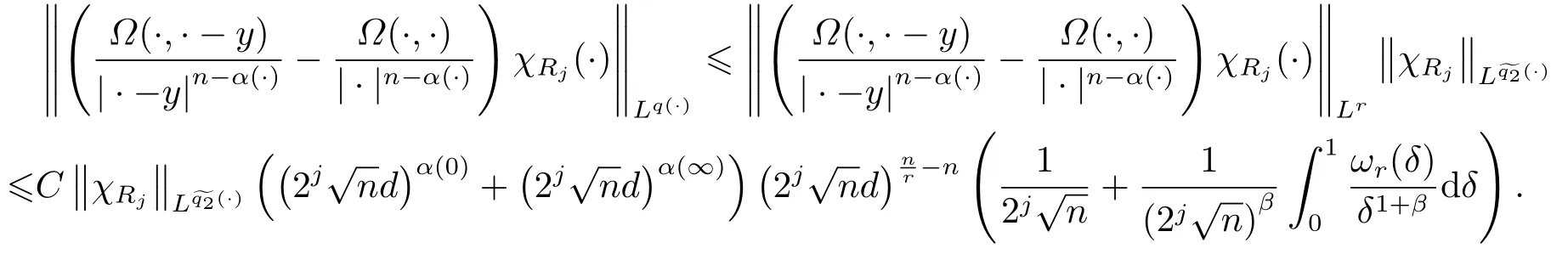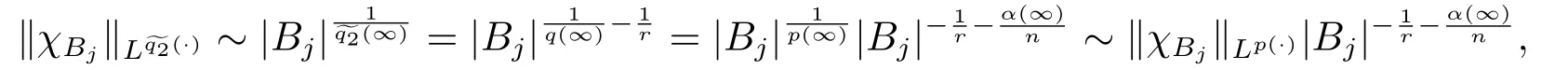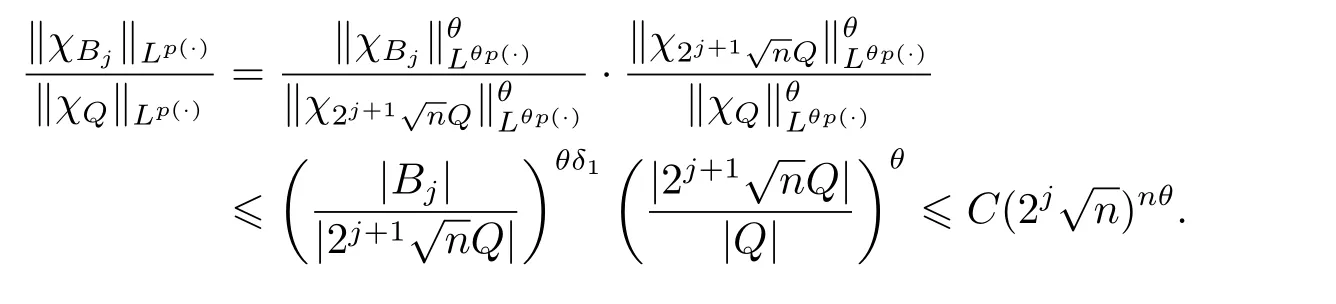Fractional Integral Operators with Variable Kernels Associate to Variable Exponents
ZHANG Zhiming(張志明),ZHAO Kai(趙凱)
(School of Mathematics and Statistics,Qingdao University,Qingdao 266071,China)
Abstract: In this paper,by the atomic decomposition of the Hardy spaces with variable exponents,using the estimates of classical inequality and the properties of the variable exponents,we proved that the fractional integral operators with variable kernels associated to variable exponents are bounded from the Hardy spaces to Lebesgue spaces with variable exponents.
Key words: Fractional integral operator;Variable kernel;Variable exponent;Hardy space
1.Introduction
The fractional integral operators should trace back to the middle of the last century.In 1955,Caldern and Zygmund[1]investigated theL2boundedness of singular integral operators with variable kernels.
LetSn?1denote the unit sphere in Rn.Suppose that? ∈Lr(Sn?1) withis homogeneous of degree zero on Rn.The homogeneous fractional integral operatorT?,α,1<α In 1971,Muckenhoupt and Wheeden[2]studied the weighted (Lp,Lq) boundedness ofT?,αfor power weight when 1 On the other hand,as we all know,Hardy spaces have been playing a central role in harmonic analysis.Here,we study the Hardy spaces with variable exponents which introduced by Nakai and Sawano[6].They established the atomic decomposition of Hardy spaces with variable exponents.Since then the Hardy spaces with variable exponents were discussed by many authors[7?8].In 2015,TAN and LIU[9]established some boundedness of homogeneous fractional integrals on some variable exponent function spaces. In this paper,by using the atomic decomposition of the Hardy spaces with variable exponents,we discuss the boundedness of the fractional integral operators with variable kernels associated with variable exponents on the Hardy spaces.For convenience,in Section 2,we recall the definitions and some properties of the variable exponent and the Hardy spaces.We show some useful lemmas of variable exponents and prove the main result in Section 3. In this section,we introduce the fractional integral operators with variable kernels,the Hardy spaces with variable exponents associated to variable exponents,and some properties of the variable exponent. Definition 2.1Suppose thatSn?1is the unit sphere in Rn,anddσis the normalized Lebesgue measure inSn?1.A function?(x,z) defined on Rn ×Rnis said to belong toL∞(Rn)×Lr(Sn?1),if it satisfies the following conditions: TheLr-Dini condition for?is as follows. Definition 2.2Suppose thatWe say that?satisfies theLr-Dini condition if the conditions 1)-3) of Definition 2.1 hold and whereωr(δ) is defined by whereρis a rotation in Rnand We say that?satisfies the strongerLr-Dini condition if (2.1) is replaced by whereβis a positive constant. The functionp(·) : Rn →(0,∞) is called the variable exponent and we adopt the standard notations in variable exponents.For a measurable subsetG ?Rn,we write We abbreviatep?(Rn) andp+(Rn) top?andp+,respectively.P0(Rn) denotes the set of measurable functionp(·):Rn →(0,∞) that satisfies LetP(Rn) denote the set of measurable functionp(·):Rn →(1,∞) such that Definition 2.3Letp(·)∈P0(Rn).f ∈Lp(·)(Rn) if and only iffis a measurable function and?λ ∈(0,∞) such that Moreover,for any B(Rn)denotes the set of measurable functionp(·)∈P(Rn)such that the Hardy-Littlewood maximal functionMis bounded onLp(·)(Rn). Lemma 2.1[10]Suppose thatp(·)∈P(Rn).Set a measurable functionf:G×G →R,satisfying for almost everywherey ∈G,f(·,y)∈Lp(·)(G).Then Lemma 2.2[6]x ∈Rn.Then for all measurable functionsfandg,there is Because the variable spaces don’t have the translation invariance,we introduce the log-Hlder continuity condition. Lemma 2.3[6]Ifp(·) satisfies the conditions we say thatp(·) satisfies the log-Hlder continuity condition,denoted byp(·)∈LH(Rn). Lemma 2.4[11]Letp(·)∈P(Rn)∩LH(Rn).Thenp(·)∈B(Rn). We useQ=Q(x,r) to denote the cube which centered atx= (x1,x2,...,xn) with sidelengthr,and we also denoteχQas the characteristic functionQ. Lemma 2.5[12]Letp(·)∈LH(Rn)∩P0(Rn),then 1) For every cubeQ,all 2) For every cubeQand Lemma 2.6[13]Forp(·)∈B(Rn),define the adjointp′(x) withThen there exist positive constantsδ1,δ2satisfying 0<δ1,δ2<1,such that for all ballsBin Rnand all measurable subsetsS ?B. Definition 2.4Letf ∈S′(Rn) andψt(x) =t?nψ(t?1x),x ∈Rn.The grand maximal function is defined by whereandNis a sufficient large integer. The Hardy space with variable exponentp(·) is defined by with Definition 2.5[6]Letp(·) :Fix an integer= min{d ∈N∪{0}:p?(n+d+1)>n}.A functionaon Rnis called a(p(·),q)-atom if there exists a cubeQ,such that The set of all such pairs (a,Q) will be denoted byA(p(·),q). Definition 2.6[6]For sequences of nonnegative numbersand cubesdefine wherep=min(p?,1). The function spaceis the set of all functionsfsuch that it can be written in the form whereis finite.One defines Define and Moreover, and Lemma 2.7[6]A trivial fact that can be deduced from the embeddingl∞is that Lemma 2.8[6]LetFor sequences of nonnegative numbers∈A(p(·),q),there is Lemma 2.9[6,9]Letp(·)∈P0(Rn)∩LH(Rn).ThenHp(·)(Rn)∩Lp++1(Rn) is dense inHp(·)(Rn). Lemma 2.10[6]Letp(·)∈P0(Rn)∩LH(Rn).Then for allf ∈S′(Rn), Let?(x,z)∈L∞(Rn)×Lr(Sn?1).The fractional integral operators with variable kernels associated to variable exponents is defined by whereα(·) is a variable exponent satisfyingα(·)∈P(Rn) andα(·)∈LH(Rn). Before stating our main result,we should give some lemmas. Lemma 3.1[8,14]Letα(·)∈P(Rn).Ifα(·) is log-Hlder continuous at the origin,then Ifα(·) is log-Hlder continuous at the infinity,then where Lemma 3.2Letα(·)∈P(Rn),1<α(·) and if ProofThe proof follows the idea of [3].We just prove the case forAnd the others are similar but easier.SinceandR<|x|<2R,we can easily get that|x ?y|~|x|.Thus, Therefore, Following Lemma 3.1,using Polar transformation and Jensen’s inequality,we obtain that Using Polar transformation and the homogeneity of?,we see that whereJust as in [3],the inner integral is bounded by whereandThen,similar to [3],we can have Therefore,Lemma 3.2 is proved. Lemma 3.3[15?16]Letα(·)∈P(Rn),α(·)∈LH(Rn).Suppose? ∈L∞(Rn)×Lr(Sn?1),satisfies theLr-Dini condition.Ifthen there exists a constantC >0 independent off,such that Our main result is as follows. Theorem 3.1Letα(·)∈P(Rn),α(·)∈LH(Rn).Supposeβ >0,andIfsatisfies the strongerLr-Dini condition,then there exists a constantC >0,such that ProofSuppose thatq ?1,which satisfies (2.3).For anyf ∈Hp(·)(Rn)∩Lp++1(Rn),applying Lemma 2.9 and (2.2),we obtain that there exist sequences of nonnegative numbersand cubessuch that and where everyajis a (p(·),q)-atom. Thus,we only need to prove that In fact,if (3.1) holds,then Lemma 2.8 and Lemma 2.7 tell us Ass√ume thatais a (p(·),q)-atom,supported in the cubeQ(cQ,d).We denoteThus, To estimate J1,since 1<α(·) Ifsimilarly,one can obtain To estimate J2,by the vanishing of atom and Lemma 2.1,we have where We will consider three cases forRj:and∞.It means thatand1 We just consider J22and the others are similar.SincesupposeandsatisfyApplying Lemma 2.2 and Lemma 3.2,we obtain that We denoteAccording to the definition of Luxemburg norm in Lebesgue space with variable exponents,it is easy to see thatFollowing Lemma 2.5,if|Bj|<1,then wherexcjis the center ofBj. And ifthen where Thus, Choosing suitableθ,such thatthenθp?>1 andθp(·)∈B(R).Therefore,by Lemma 2.6 ,the following estimate holds. Hence,noting thatnθ ?n ?1<0 andnθ ?n ?β <0,together with three cases,we can obtain Thus,(3.1) is proved.And then,the proof of Theorem 3.1 is completed.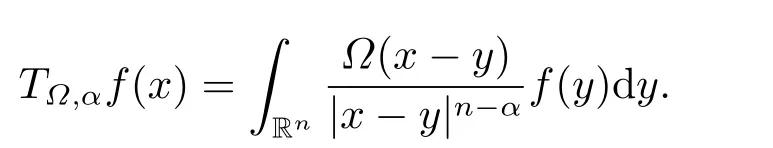
2.Preliminaries



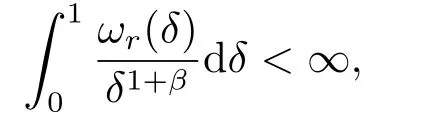
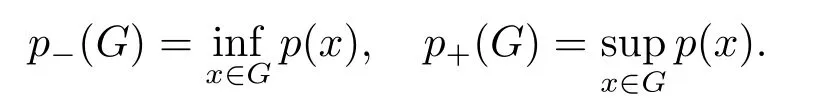


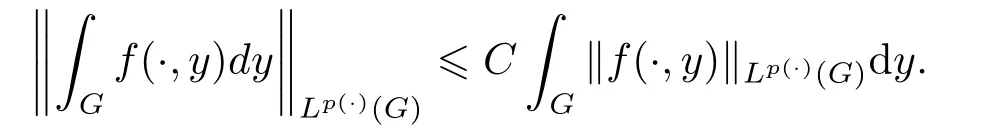
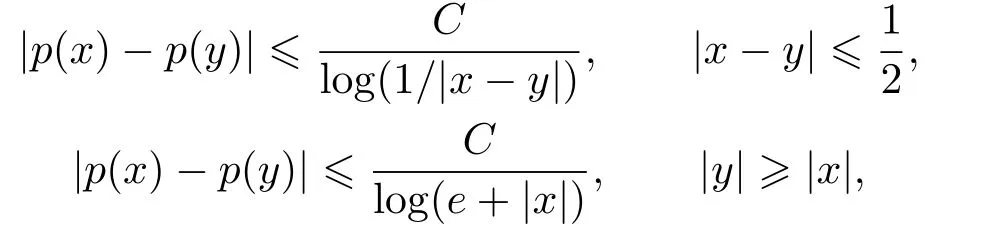


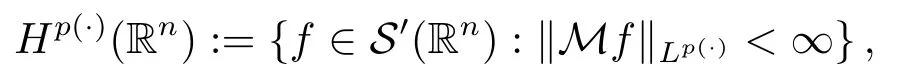
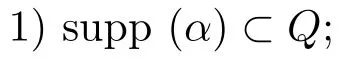



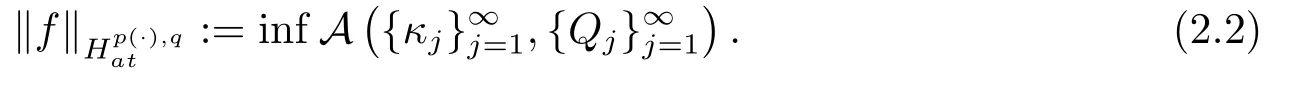
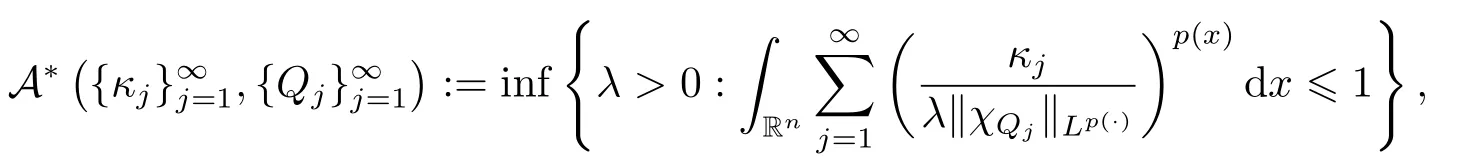


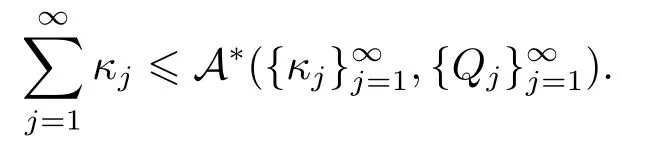
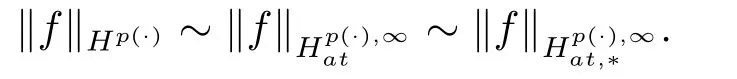


3.Main Result