華義平

(池州學(xué)院數(shù)學(xué)計(jì)算機(jī)科學(xué)系,安徽池州 247000)

共形平坦黎曼流形上的Schou ten張量

華義平

(池州學(xué)院數(shù)學(xué)計(jì)算機(jī)科學(xué)系,安徽池州 247000)

M是一個(gè)緊致的局部共形平坦黎曼流形,其上定義的Schouten張量是一個(gè)Codazzi張量.本文借助這個(gè)Codazzi張量引入Cheng和Yau的自伴算子,從而獲得了局部共形平坦流形上的一些性質(zhì),改進(jìn)了已有的結(jié)論.

局部共形平坦;Schouten張量;Ricci曲率;數(shù)量曲率

1 引言

文獻(xiàn)[1]研究了具有非負(fù)截面曲率的共形平坦黎曼流形,得到了:

定理1M為緊致共形平坦流形,如果M具有常數(shù)量曲率及非負(fù)截面曲率,則M為常截面曲率流形或者M(jìn)可以表成一個(gè)常截面曲率流形和一個(gè)一維黎曼流形的乘積.

本文繼續(xù)對(duì)局部共形平坦黎曼流形進(jìn)行研究,將定理1中截面曲率非負(fù)削弱為Ricci曲率非負(fù),得到了:

定理2M為緊致共形平坦黎曼流形,若M的Ricci曲率非負(fù),且其中S為Schouten張量,?、tr S分別表示梯度算子和S的跡,則M可以表示為空間形式或者Sn-1(c)×R.

推論1M為緊致共形平坦的具有非負(fù)常數(shù)量曲率的黎曼流形,若則M可以表示為空間形式或者Sn-1(c)×R.

推論2M為緊致共形平坦的具有常數(shù)量曲率的黎曼流形,若M的Ricci曲率非負(fù),則M可以表示為空間形式或者Sn-1(c)×R.

注推論2中蘊(yùn)含了定理1.

推論3M為緊致共形平坦黎曼流形,若M的Ricci曲率非負(fù),且

則M可以表示為空間形式或者Sn-1(c)×R.

推論4M為緊致共形平坦黎曼流形,若M的Ricci曲率非負(fù),且

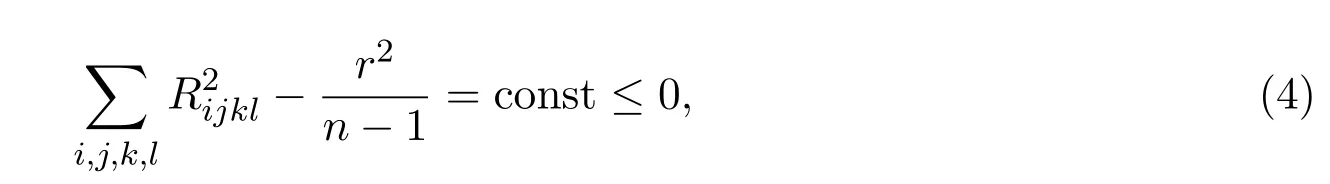
則M可以表示為空間形式或者Sn-1(c)×R.

2 預(yù)備知識(shí)

令M為n維黎曼流形,e1,e2,…,en為M上的局部標(biāo)架場,w1,w2,…,wn為其對(duì)偶標(biāo)架場,M的結(jié)構(gòu)方程為:

其中wij是M的Levi-civita聯(lián)絡(luò),Rijkl是M的黎曼曲率.

如下定義的張量在度量的共形變換下不變,稱其為Weyl共形曲率張量[2]:

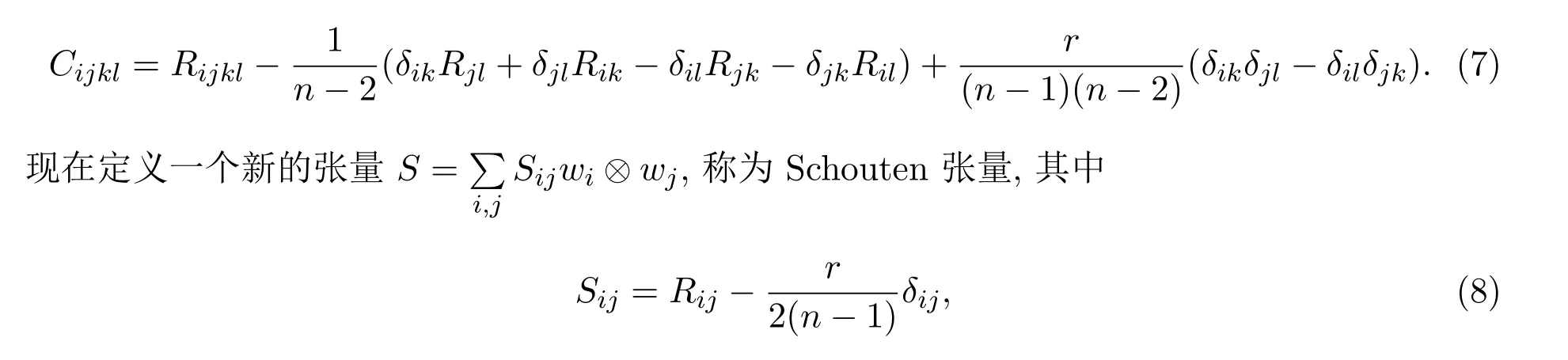
顯然Sij=Sji,并且(7)式可以表示成:

當(dāng)M為共形平坦黎曼流形時(shí),有

即S是一個(gè)Codazzi張量,于是引入□[3]算子:

其中f∈C2(M,R),可以驗(yàn)證□是關(guān)于M的L2-內(nèi)積自伴的[4],即

在P∈M點(diǎn)附近選取標(biāo)準(zhǔn)正交標(biāo)架場e1,e2,…,en,使得Sij=λiδij,則(13)式可以簡化為:

通過對(duì)(14)式積分得到[5]:

引理1[6]若M的數(shù)量曲率非負(fù),且Ricci張量滿足:

則M的Ricci曲率非負(fù).

引理2[7]等式

蘊(yùn)涵著下面的不等式

直接計(jì)算有

引理3令M為共形平坦黎曼流形,如果

則(17)式成立.

3 定理的證明

由于Ricci曲率非負(fù),因此不妨設(shè)0≤ρ1≤ρ2≤…≤ρn,于是當(dāng)i＜j＜k時(shí),

結(jié)合(26)式命題成立.

從命題的證明過程中知,(20)式取等號(hào)當(dāng)且僅當(dāng)

根據(jù)定理?xiàng)l件,結(jié)合(15)式,從而M為常曲率的或者為Sn-1(c)×R.這就完成了定理2的證明.

由引理2,引理3知推論3,推論4分別成立.

[1]紀(jì)楠,閻少宏,彭亞綿.共形對(duì)稱黎曼流形上的Codazzi張量及其應(yīng)用[J].河北理工大學(xué)學(xué)報(bào),2007,29(3):110-113.

[2]宋衛(wèi)東,劉敏.關(guān)于局部對(duì)稱共形平坦空間中具有常數(shù)量曲率的子流形[J].數(shù)學(xué)物理學(xué)報(bào):A輯,2010,30 (4):1102-1110.

[3]朱業(yè)成,宋衛(wèi)東.de Sitter空間中具有常數(shù)量曲率的類空超曲面[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2008,24(4):788-792.

[4]Wei Guoxin.Com p lete hypersurfaces with Hk=0 in a unit sphere[J].Differential Geom etry and its app lications,2007,25:500-505.

[5]Li Haizhong.Global rigidity theorem s of hypersurface[J].A rk.Mat.,1997,35:327-351.

[6]Hu Zejun,Li Haizhong,Udo Simon.Schouten curvature functions on locally conformally flat Riemannian m anifolds[J].J.Geom.,2008,88:75-100.

[7]Cheng SY,Yau S T.Hypersurfaceswith constant scalar curvature[J].Math.Ann.,1977,225:195-204.

Schouten tensor on the locally conformally flat manifold

Hua Yiping
(Departm ent of Mathem atics and Com puter Science,Chizhou College,Chizhou 247000,China)

A com pact locally conformally flat Riemannianmanifold Mwas considered,The Schouten tensor on Mis a Codazzi tensor.In this paper,som e new propertieswere obtained by introducing Cheng-Yau′s self-ad joint operator on locally conform ally flat Riem annian m anifold,which im prove known conclusion.

locally con formally flat,schouten tensor,ricci curvature,scalar curvature

O186.12

A

1008-5513(2012)03-0308-05

2012-04-03.

池州學(xué)院研究生啟動(dòng)項(xiàng)目(2010RC 019).

華義平(1982-),碩士,研究方向：微分幾何.

2010 MSC:53C20