鄭國彪

(青海民族學(xué)院學(xué)報編輯部,青海西寧 810000)

關(guān)于D-完全一致混合超圖上色數(shù)的一個結(jié)論的推廣

鄭國彪

(青海民族學(xué)院學(xué)報編輯部,青海西寧 810000)

混合超圖的上、下色數(shù)的研究是超圖研究中一個重要的話題.由于超圖本身結(jié)構(gòu)上的復(fù)雜性,近年來對超圖色性的研究也近局限于對一些特殊圖類的研究,其中完全一致混合超圖是最為熱門的圖類之一.給出了D完全(C不完全)一致混合超圖的概念,并運用組合數(shù)學(xué)中有關(guān)分劃的思想和方法對該圖類的色性進行了進一步的研究,對相關(guān)文獻中給出的結(jié)論進行了推廣,得到了一個較為一般化的結(jié)論.并在該定理的證明中得到并證明了一個關(guān)于混合超圖C穩(wěn)定集的重要論斷,對超圖色性研究有著重要的意義.

D-完全一致混合超圖;上色數(shù);下色數(shù)

1 基本概念及引理

則K(n,l,m)稱為n個頂點的完全(l,m)-一致混合超圖.顯然,對于給定的n,l,m,在同構(gòu)的意義下恰好存在一個K(n,l,m).

定義1.2[2-3]混合超圖H=(X,C,D)的存在嚴格i-著色的所有i中最大的i稱為H的上色數(shù),表示為(H).

定義1.3[1]如果混合超圖H=(X,C,D)的頂點集X的一個i分劃X=(X1,X2,…,Xi)滿足:

1)每一條C-超邊至少有兩個頂點在同一個分劃塊中;

2)每一條D-超邊至少有兩個頂點在不同的分劃塊中.

則該分劃被稱為H的可行性分劃.

顯然,H的任一嚴格i著色都對應(yīng)著某一嚴格i可行性分劃,反之亦然.因而二者是等價的.可將H的一個可行性分劃或一嚴格i-著色c表示為:

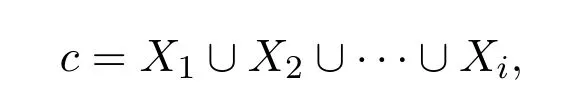
并用ri(H)=ri表示可行性i分劃的個數(shù).

定義1.4[1]混合超圖H=(X,C,D)的頂點集X的一個子集S如果不包含任何一條C-超邊(D-超邊)作為其子集,則稱其為C穩(wěn)定的或C獨立的(D穩(wěn)定的或D獨立的).

定義1.5[1]如果H的正常i-著色中,i種顏色都被用到,那么這一著色被稱為嚴格的i-著色.

顯然,對于可著色的混合超圖H,一個正常的χ(H)-著色一定是一嚴格著色.

定義1.6[1]在混合超圖H=(X,C,D)的任一著色c中,頂點集X的子集Y,如果滿足:對任意的y1∈Y,y2∈Y,有c(y1)=c(y2),則稱子集Y是單色的;如果每兩點的顏色都不相同,即c(y1)/=c(y2),則稱子集Y是多色的.

由混合超圖正常著色的定義可知,在混合超圖的任一正常著色中,D-超邊一定是非單色的子集,C-超邊一定是非多色的子集.

定義1.7[1]H的任意一個嚴格i-著色都導(dǎo)出一個頂點集X的i分劃,每一個分劃塊是一非空單色子集,稱為色類.

定義1.8[1]混合超圖H=(X,C,D)的頂點集X的一個子集S如果不包含任何一條C-超邊(D-超邊)作為其子集,則稱其為C穩(wěn)定的或C獨立的(D穩(wěn)定的或D獨立的).

引理1.1[4]混合超圖

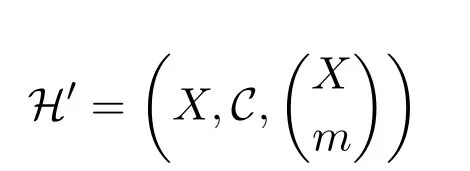
2 主要結(jié)果

即當p=1時,結(jié)論成立.

假設(shè)對任意p＜t結(jié)論成立.則當p=t時,即從色類X1中取出t個頂點重新分配到其它色類且保持關(guān)系|Xj1|≥|Xj2|≥…≥|Xji|.不妨設(shè)第t次從X1中取出的頂點為x′(l+k-t-r),將它重新分配到色類Xj中.并設(shè)在此之前色類X2,…,Xj-1,Xj,Xj+1,…,Xr中所包含的頂點數(shù)分別為:n2,…,nj-1,nj,nj+1,…,nr,同時在此步操作前色類X1中的頂點數(shù)為l+k-r-t+1,則此步操作后各色類中的頂點數(shù)分別是:

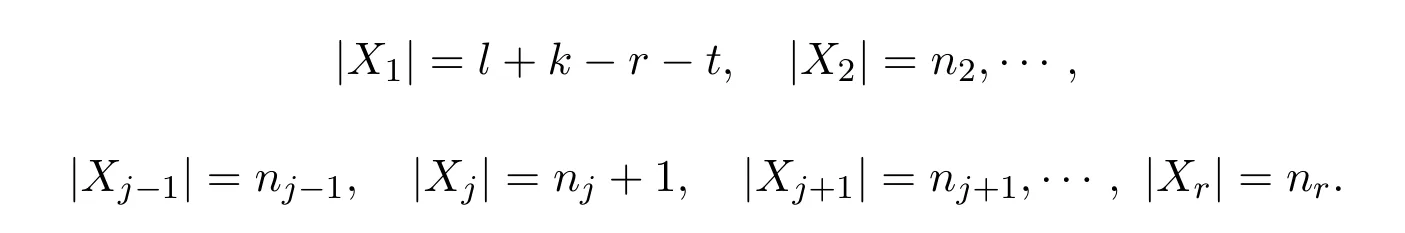
易知第t-1步操作后,所得可行性分劃對應(yīng)的s的值為:

第t步操作后,所得可行性分劃對應(yīng)的s的值為:

又因為根據(jù)證明開始時的約定,第t步操作后,色類X1中的頂點數(shù)(l+k-r-t)不小于

其它任何一個色類中的頂點數(shù),即:l+k-r-t≥nj+1,從而

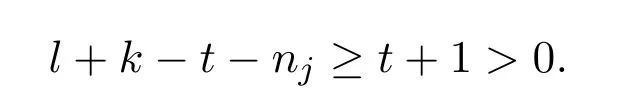
所以,第t步操作后,所得可行性分劃對應(yīng)的s的值:

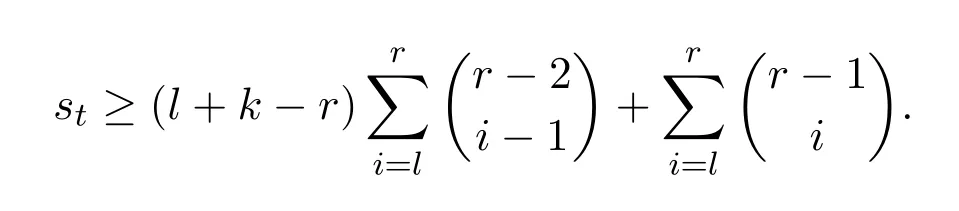
即當p=t時,結(jié)論也成立.

綜上可知,斷言對任意自然數(shù)p都成立.

在已證上述斷言的基礎(chǔ)上,下面再來證本定理結(jié)論.

顯然,由斷言容易得到下述結(jié)論:

[1]V italy,Voloshin V I.Coloring Mixed Hypergraphs:Theory,A lgorithm s and App lications[M].Rhode Island: Am erican Mathem atical Society Providence,2003.

[2]Voloshin V I.Them ixed hypergraphs[J].Com put.Sci.J.Moldova,1993(1):45-52.

[3]Voloshin V I.On the Upper Chrom atic Number of a Hypergraph[M].Chisinau:Preprint of Moldova State University,1992.

[4]鄭國彪.一類一致混合超圖的上、下色數(shù)[J].青海師專學(xué)報,2007(5):18-22.

[5]鄭國彪.關(guān)于刪除若干C-超邊的完全一致混合超圖色數(shù)的幾個結(jié)論[J].青海師專學(xué)報,2008(5):12-15.

[6]鄭國彪.D-完全一致混合超圖不可著色的一個充要條件[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2011,27(3):308-312.

Generalized extend of one result of the upper chromatical number of the D-complete uniform mixed hypergraph

Zheng Guobiao
(Editer Department of Qinghai Nationalities Institutes,Xining 810000,China)

It is aimportant topic to study the upper and lower chrom atical number of them ixed hypergraphs. As the hypergraphs have a complex structure,all study on chrom atical properties of the hypergraphs are lim ited to only some special kind of hypergraphs.The com p lete uniform m ixed hypergraph is themost popular one am ong they.In this artical,a new concept that the D-com p lete uniform m ixed hypergraph was given,and further studied its the upper chrom atical number on previously a initial result basis,and ageneral result was attained.In the course of proving this conclusion,we find and prove a important predication connection with the stable set of them ixed hypergraphs,which has a im portant m ean.

the D-com plete uniform mixed hypergraphs,upper chrom atic number, lower chromatic number,extend elementary method,conjecture

O157

A

1008-5513(2012)03-0294-09

2012-02-03.

青海省自然科學(xué)基金(2001-Z-911).

鄭國彪(1967-),碩士,副教授,研究方向：圖論及其應(yīng)用.

2010 MSC:05C78